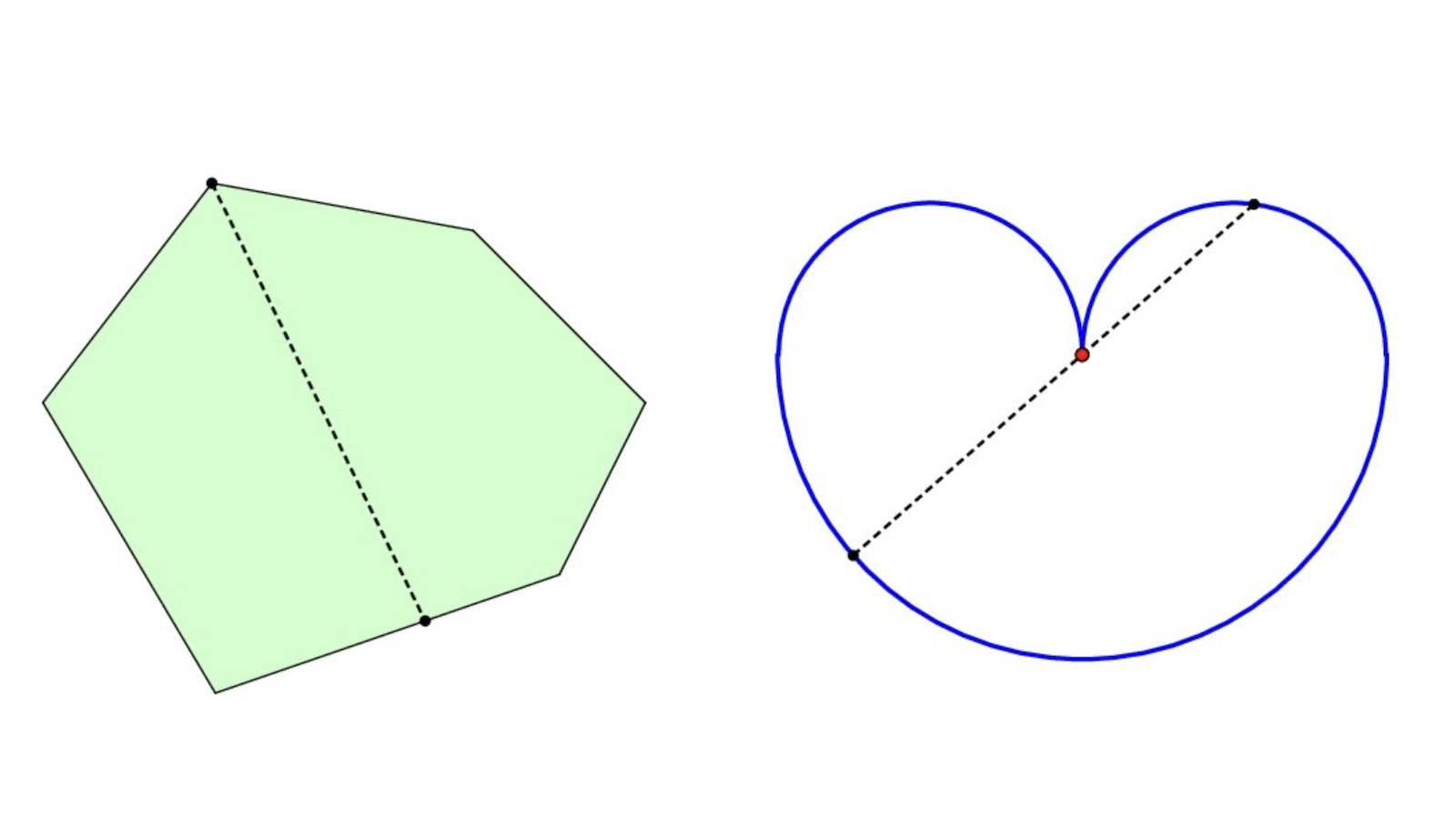
Partager une figure du plan en deux parties « égales » (en un sens à préciser suivant le contexte) est une question naturelle en géométrie euclidienne. Dans cet article nous nous sommes intéressés au partage par une droite d’un polygone en deux sous-polygones de même aire, et nous y avons indiqué comment procéder géométriquement à la règle et au compas dans le cas du triangle et du quadrilatère. Intéressons-nous maintenant aux longueurs des courbes : comment partager une courbe fermée du plan en deux courbes de même longueur ?
Nous vous invitons à télécharger le pdf pour lire la totalité de l'article
ÉCRIT PAR
Aziz El Kacimi
Professeur émérite - Université Polytechnique Hauts-de-France
12h02
Bonjour. La contrainte de partage d’une courbe en deux courbes connexes par toute droite passant par un centre d’équitabilité permet de considérer que cette courbe admet une paramétrisation polaire r = f(θ). Si f est au moins continue et dérivable par morceaux (ce qui est bien le cas de la figure avec trois demi-cercles), le parcours de la courbe en fonction de l’angle a un vecteur vitesse dont le carré de la norme est alors v² = f² + f′², et on obtient bien un centre d’équitabilité si et seulement si v est π-périodique.
Si f est constante de valeur R sur un demi-tour (comme le long de l’arc de cercle sous la ligne horizontale de la figure de l’article), la vitesse est constante de même valeur et la fonction f doit satisfaire une équation différentielle
f′ = ±√(R² − f²), dont les solutions non constantes sur chaque intervalle de dérivabilité sont de la forme
f(θ) = R cos(±θ + θ₀). On reconnait l’équation polaire d’un cercle de rayon R/2 avec le point O sur son bord.
Cela nous permet de construire une infinité de courbes solutions, par exemple le bord de n’importe quel union finie de disques de même rayon et dont les centres sont à même distance d’un point O à l’intérieur de leur enveloppe convexe. On peut ainsi construire un joli triskell par exemple.
Plus généralement, l’ensemble de ces courbes peut être paramétré par l’ensemble des fonctions continues et affines par morceaux, 2π-périodiques, positives et dont la valeur absolue de la dérivée est constante en dehors des intervalles sur lesquels la fonction est égale à sa valeur maximale.
Mais ces solutions ne couvrent que le cas très particulier d’une trajectoire à vitesse constante par paramétrisation par l’angle. Existe-t-il des solutions pour n’importe quelle fonction v continue, π-périodique et dérivable par morceaux ?