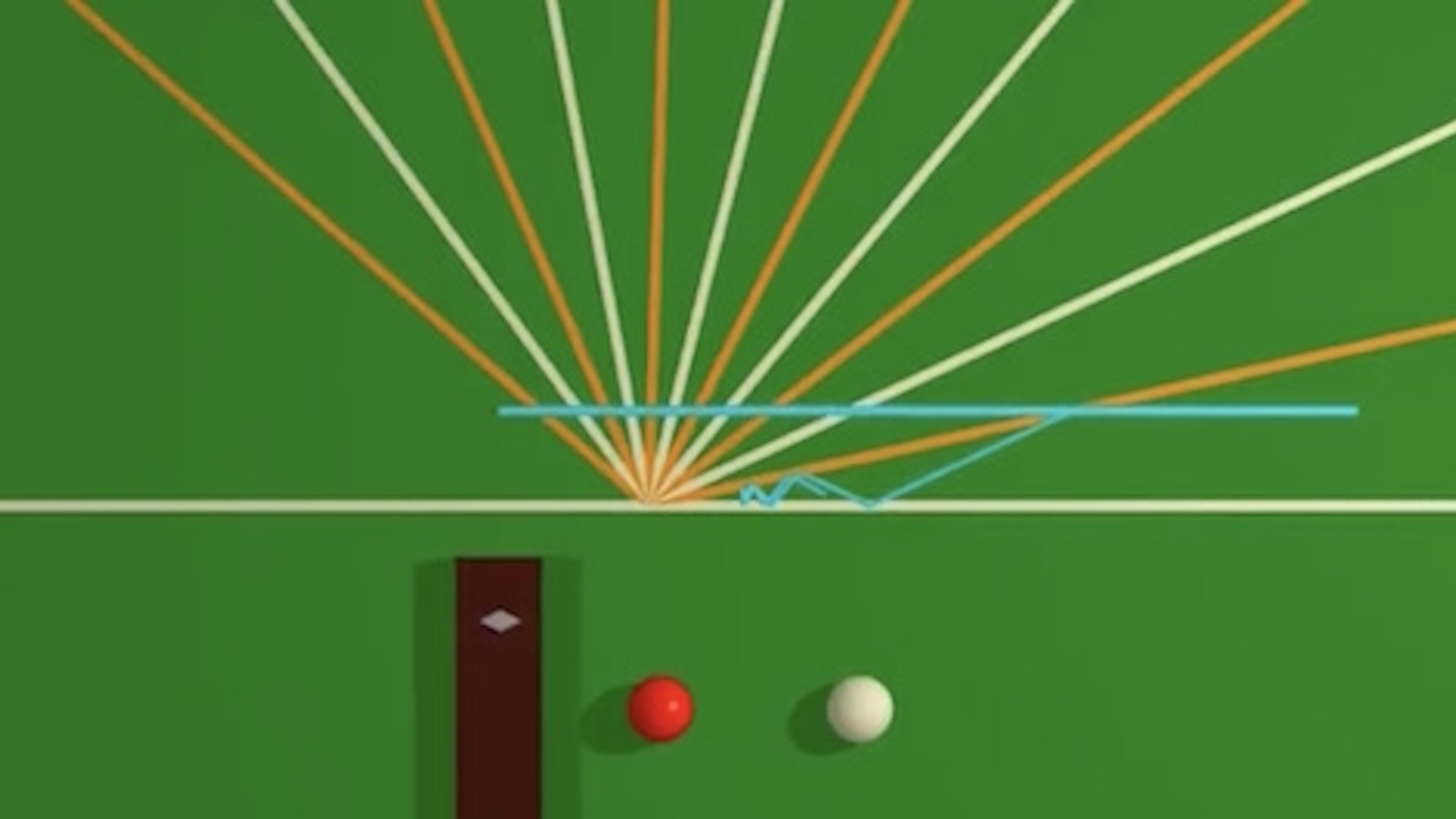
Dans l’article Deux billes, une bande et des rebonds et à la suite de vidéos publiées sur la chaîne YouTube 3Blue1Brown [1], nous nous sommes intéressés au nombre de rebonds entre deux billes de billard et une bande de ce dernier. Quelques expérimentations numériques nous ont même permis de conjecturer le comportement asymptotique du nombre de rebonds N avec une formule particulièrement simple ne dépendant que du rapport μ des masses des billes et faisant étonnamment apparaître le nombre π :
\[N=N(\mu) \underset{\mu \to +\infty}{\sim} \pi \sqrt{\mu}\]
Nous allons voir dans cet article comment calculer précisément le nombre total de rebonds dans le cadre de la dynamique newtonienne de trois manières différentes. Dans les deux premières approches, nous allons « géométriser » le problème et le réinterpréter comme un système dynamique continu ou comme un système dynamique discret. La troisième approche est une résolution purement algébrique.
ÉCRIT PAR
Aurélien Alvarez
Professeur - Rédacteur en chef d'IdM - École normale supérieure de Lyon
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.