Elles ont bercé nos premiers pas en géométrie et calcul différentiel, et pourtant aujourd’hui elles sont souvent absentes des cursus universitaires : ce sont les courbes et surfaces remarquables, la lemniscate de Bernoulli, la parabole semi-cubique, la brachistochrone… Un site ouaibe remarquable (et en français) leur est consacré : www.mathcurve.com. C’est un lieu de promenade agréable pour les moments de loisir de l’amateur de jolies formes, et une source d’exemples inépuisable pour l’enseignant.
ÉCRIT PAR
Jean-Yves Briend
Maître de conférences - Université de Provence
9h51
En math sup , nous avons eu ce genre d’exercice vicieux (merci Monsieur Richard 😀 ) :
« On vous donne trois cercles de biseaux de même rayon. La courbure du triangle concave obtenu est-elle égale à celle d’un hypocycloïde à trois sommets ? Si oui, quelle en est la preuve ? »
J’ai tout de suite pensé à un deltoïde vu sur https://www.mathcurve.com/courbes2d.gb/deltoid/deltoid.shtml et sur Upme.fr pour résoudre cet exercice.
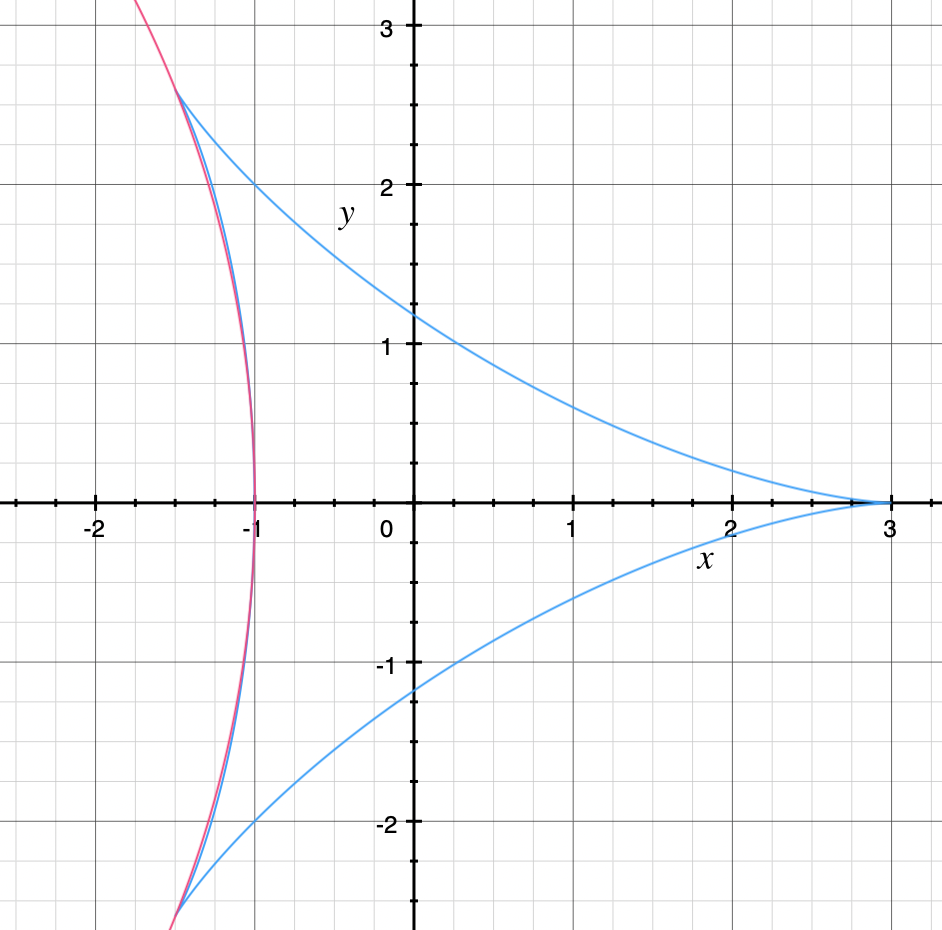
On dirait qu’un hypocycloïde à trois sommets, aussi appelé deltoïde, est constitué des arcs de trois cercles, mais ce n’est pas le cas. Voici un deltoïde en bleu, et un cercle passant par deux sommets et un « point milieu » entre eux en rouge (voir image 1 en pj).
La courbure du triangle concave dont les côtés sont des arcs de trois cercles de rayon égal est constante étant les réciproques de ce rayon.
Un deltoïde n’a pas une courbure constante.
Une évolution d’une courbe est constituée des centres de courbure de cette courbe.
Dans le cas de l’arc de cercle, l’évolution est constituée uniquement du centre de ce cercle. Ainsi pour le triangle concave dont les côtés sont des arcs de trois cercles, son évoluée est constituée des centres de ces cercles.
L’évolution d’un deltoïde est, étonnamment, un autre deltoïde.
