Un exposé de S. Smirnov

• Écho de la recherche

Aujourd’hui, le nouveau médaillé Fields Stanislav Smirnov a donné sa conférence plénière.

Le voici, accompagné de son « président de séance », le professeur Kesten, quelques secondes avant le début de son exposé.

S. Smirnov

Le contenu de l’exposé est bien sûr un peu trop technique pour être discuté dans Images des Maths. Je vais me contenter de citer l’un des résultats qu’il a cités, démontré il y a à peine quelques mois, en collaboration avec Hugo Duminil-Copin. ¹On peut également lire cet article sur Les travaux de Stanislas Smirnov.

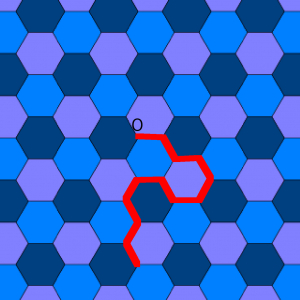
Recouvrez le plan avec des hexagones réguliers, comme sur cette figure.

.

Maintenant, partez d’un sommet, par exemple le point 0, et cherchez à vous déplacer en suivant \(N\) côtés d’hexagones avec une seule condition : il est interdit de repasser par où on est déjà passé. Par exemple, j’ai dessiné en rouge un chemin de longueur 12. De combien de manières peut-on le faire ? Appelons \(F(N)\) ce nombre. Il n’est pas question de trouver une formule pour \(F(N)\) mais on peut chercher à comprendre à quelle vitesse \(F(N)\) croît quand \(N\) tend vers l’infini. On suspecte une croissance de type exponentielle, c’est-à-dire qu’on pense que \(F(N)\) est de l’ordre de \(c^N\) pour une certaine constante \(c\) inconnue qui s’appelle la constante de connectivité. Eh bien, les auteurs ont trouvé cette constante ; elle vaut \(\sqrt{2 + \sqrt{2}}\)²Plus précisément, ils montrent que la limite de \(F(N) ^{1/N}\) quand \(N\) tend vers l’infini est \(\sqrt{2 + \sqrt{2}}\)..

Cela semble un petit problème amusant (et d’une certaine façon c’est le cas) mais ce genre de résultats est important dans des problèmes de physique statistique.