Un crayon… mais un crayon pensant !

• Maths et art

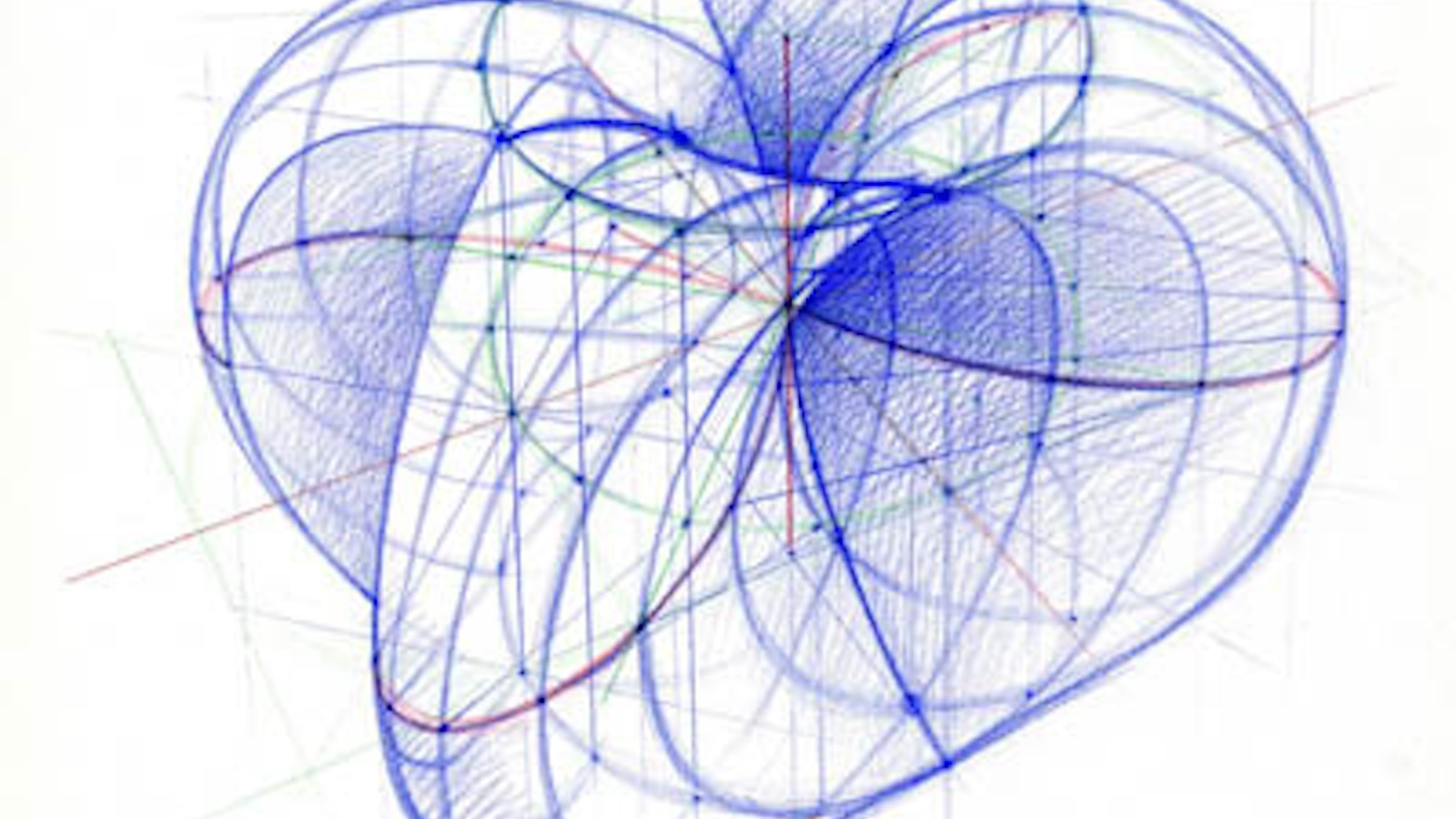
Sylvie Pic est une artiste dont le travail entre parfaitement dans la mixité entre art et mathématique que nous souhaitons présenter ici.

Sylvie n’a pas suivi de formation mathématique. Elle quitte le lycée après la classe de seconde et entre à l’école des beaux arts de Marseille. Autant dire qu’à cette époque, son intérêt allait plutôt vers l’art plastique que vers les sciences. Mais aux beaux arts, elle se sentait mal à l’aise, en porte-à-faux par rapport à ce qu’alors (les années 70) on y enseignait ¹À cette époque l’orientation était plutôt « Support Surface » ; un courant d’art qui rejetait le contenu de la toile et portait son attention et action sur le contenant, pourrai-je dire en résumant de manière outrancière … mais il faut faire court car là n’est pas mon objet..

Sylvie a pratiqué le dessin, la perspective, forcément de façon un peu anachronique et isolée en cette école. Cela lui permit entre autre de l’exploiter au sortir de l’école puisqu’elle assura son alimentaire dans des cabinets d’architectes où, l’informatique n’étant pas encore d’usage, on représentait et dessinait encore à la main. Sans nul doute cela lui affermit la main mais cela dut nourrir des réflexions géométriques car depuis qu’elle a décidé de ne se consacrer qu’à son activité artistique, c’est d’espaces qu’elle nous entretient. Son voyage dans l’univers mathématique se fait avec le crayon … et sans nul doute, en partie cachée, une culture mathématique et philosophique qu’elle nourrit de nombreuses lectures. Bien évidemment si vous lui parlez topologie elle aura du répondant, mais ne lui parlez pas de topologie algébrique … elle n’est pas mathématicienne en ce sens là. Ce sont les formes, le visuel, le geste du dessin, le crayon qui animent son esprit.

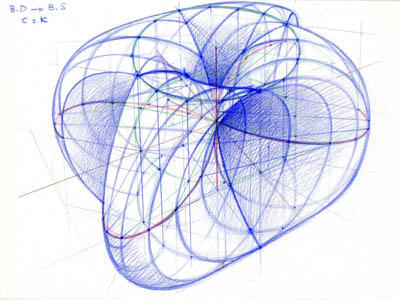
Ce n’est qu’un crayon mais un crayon pensant. Un crayon qui plie mais ne rompt pas. Et … fi de ces matières synthétiques aux performances étonnantes qui manquent de sensibilité. Le papier, également, sur lequel elle vient avec son crayon coucher ses pensées géométriques a une sensualité. Ce n’est pas un vulgaire papier couché mais un papier qui a de la fibre … sensible. Car c’est bien là sa richesse dans le domaine de la mixité art-mathématique, elle réussit à donner de la sensibilité, de la sensualité à des propositions géométriques. Comme toute proposition mathématique il n’est pas évident de déchiffrer le message à la simple lecture, si nous ne sommes pas préparés.

Devant ces dessins il apparaît clairement que ce sont des tableaux dans le sens habituel que l’on donne à une production d’artiste. C’est d’abord l’émotion qui nous pénètre. Ensuite, si vous êtes spécialiste des sujets qu’elle traite, vous entrerez en dialogue avec la proposition mathématique. Mais même si vous n’avez aucun attrait pour les mathématiques, il n’est pas évident que vous n’ayez pas l’envie de posséder un de ces exemples sur votre mur. C’est en cela que je dis qu’elle accomplit bien la mixité art-mathématique.

Je ne saurai (ici, en quelques mots) vous entretenir de ce qu’il y a en partie cachée dans ses pensées.

Est-ce si grave ? Je ne pense pas, car c’est d’art visuel qu’il s’agit ici en premier. Le message de la sensibilité qui transite par l’œil jusqu’à l’émotion traverse bien sûr le cerveau mais ne s’exprime pas avec des mots … Sinon pourquoi toute cette peine, car il y a de l’ouvrage pour aboutir un tableau.

Chez Sylvie il ne s’agit donc pas seulement d’illustrer une proposition géométrique. Car, si c’était le cas, elle se serait mise à l’informatique et ses outils qui permettent de réaliser rapidement des images mathématiques complexes. Il s’agit d’être artiste dans la réalisation ; la réalisation d’une pensée qui accompagne et se nourrit de la lenteur et de la délicatesse d’une caresse. Une caresse qui passe et repasse mille fois au même endroit, l’enrichissant chaque fois (ou bien le détruisant parfois, hélas !) d’un petit rien qui sera évident … la chose achevée.

Deux liens qui vous permettront de faire plus ample connaissance avec son travail : 1 et 2.