
Et les vainqueurs sont…
Nous avions lancé sur ce site aux mois de novembre et décembre derniers une compétition d’images en lien avec l’exposition itinérante Imaginary qui s’était installée dans les bibliothèques de mathématiques-informatique recherche de l’UPMC (Paris 6) à Jussieu et de l’UPD (Paris 7, site de Chevaleret). Rappelez-vous le billet de Bernard Teissier.
Nous avons reçu une trentaine d’images (presque toutes générées grâce au logiciel Surfer) pour cette compétition et nous tenons à souligner la qualité et l’originalité de l’ensemble des images proposées. Le choix ne fut pas simple et le jury, composé de Jos Leys, Bernard Teissier et moi-même, a choisi d’attribuer le premier prix à Hiltrud Heinrich pour son image «L’être originaire dans l’œuf».

L’être originaire dans l’œuf
Comme je suis sûr que certains d’entre vous aiment les équations, je ne résiste pas à vous donner celle de «L’être originaire dans l’œuf» :
\[ ((x^2+y^2+z^2-9)^3-x^2y^2z^2)(x^2+y^2+z^2-0,5)xy^2+yx^2+xz=0\]
Rappelons que ce premier prix était doté d’un montant de 50 euros et du jeu Plato’s Solids de Zoomtool.
Le second prix d’un montant de 40 euros accompagné du catalogue de l’exposition Imaginary a, quant à lui, été attribué à Mehrdad Garousi pour son image «Standing Mathematical Sculpture» à l’équation sulfureuse :
\[(x^2+y^2+z^2-(0.5+2a)^2)^2-\frac{(3(0.5+2a)^2-1)}{(3-(0.5+2a)^2)}(1-z-\sqrt{3}x)(1-z+\sqrt{3}x)(1+z+\sqrt{3}y)(1+z-\sqrt{3}y)=0,\]
où \(a\) est un paramètre réel positif petit (autour de 0,1 disons).
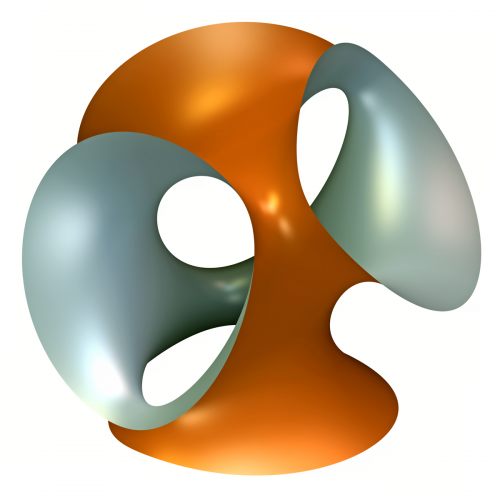
Standing Mathematical Sculpture
Retrouvez toutes les images qui ont été soumises en suivant le lien «Galerie du concours» dans le billet annonciateur de l’événement.
À très bientôt pour une prochaine compétition… mathématico-artistique. 🙂



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.