
Dans la vie d’un chercheur en mathématiques, il arrive qu’un ami vienne vous poser un problème, en imaginant que vous seriez la personne la plus à même d’y répondre. Plus rarement, vous pouvez effectivement apporter des réponses et trouver le problème intéressant…
l s’agit d’un problème amené par mon frère. Dans le club de volleyball qu’il anime, l’entraînement a lieu dans un gymnase contenant 3 terrains. Les joueurs se répartissent en 6 équipes, de sorte à pouvoir jouer 3 matchs simultanés. Une fois que cette première phase de 3 matchs est terminée, les équipes se répartissent différemment sur les terrains, de sorte à jouer 3 nouveaux matchs. Ainsi a lieu cette deuxième phase de 3 matchs, puis la troisième, etc. C’est en général à la quatrième phase de jeux que les soucis commencent. Il n’arrive plus à programmer 3 « nouveaux matchs », et deux équipes qui ont déjà joué ensemble sont donc contraintes de jouer de nouveau ensemble. Y a-t-il une manière d’éviter cela ? Comment s’y prendre ?
Pour répondre à ce problème, on peut donner un nom à chacune des équipes, et essayer d’écrire le planning des matchs à jouer. Peut-être même peut-on arriver à y répondre, avec un peu de patience. Ceci dit, le problème est sans doute plus facile à visualiser en utilisant des graphes. Je propose de regarder le graphe complet à 6 sommets, que l’on peut représenter ainsi :

Figure 1
Chaque sommet de ce graphe représente une équipe. Chaque arête reliant deux sommets représente un match entre les 2 équipes concernées. Lors d’une phase de jeux, 3 matchs ont lieu en simultané, sur les 3 terrains. Ces 3 matchs correspondent donc à 3 arêtes du graphe. Ces 3 arêtes ne sont pas quelconques puisque chaque sommet du graphe doit être incident à exactement une arête (car chaque équipe est en train de jouer un match). En théorie des graphes, on dit que ces arêtes forment un couplage parfait du graphe.
On peut décrire le déroulement de la séance d’entraînement ainsi. La première phase correspond à un couplage parfait du graphe complet. Puis la deuxième phase correspond à un couplage parfait… du graphe dans lequel on a supprimé les arêtes intervenant dans la première manche. Eh oui, on ne veut pas rejouer un même match ! À chaque phase de jeux, on continue ainsi à supprimer des arêtes… jusqu’à ce qu’on ne puisse plus trouver de couplage parfait. La question devient alors de voir quand cela arrive, et comment faire pour que cela arrive le plus tard possible.
Avec cette reformulation, il est, me semble-t-il, plus simple de comprendre quels sont les scénarios possibles. En effet, après deux phases de jeux, quitte à réordonner les équipes comme il le faut, on peut toujours se débrouiller pour que les 6 arêtes correspondant aux matchs joués lors des deux premières phases ne soient autres que les 6 côtés de l’hexagone. On obtient ainsi la figure suivante :
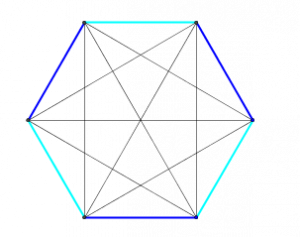
Figure 2
Dans cette figure et les suivantes, au lieu de supprimer les arêtes des phases passées, je les ai coloriées, d’une couleur pour chaque phase. Les arêtes noires correspondent donc aux matchs qui n’ont pas encore été joués. Maintenant, deux scénarios bien distincts peuvent se produire. Dans le premier, la phase suivante correspond aux 3 grandes diagonales de l’hexagone, la situation étant alors représentée ainsi :
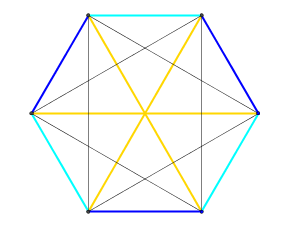
Figure 3
Et là, c’est fini ! On ne peut plus trouver de couplage parfait avec les seules arêtes noires. C’est la situation à laquelle arrivaient apparemment le plus souvent les équipes du club de volley…
Le deuxième scénario est par contre plus favorable. En effet, si la 3e phase ne correspond pas aux 3 grandes diagonales, on se convainc facilement que l’on pourra forcément effectuer une 4e, et même une 5e phase de jeux, les 5 phases étant alors représentées ainsi :

Figure 4
Au final, en 5 phases de jeux, chacune des 6 équipes aura rencontré les 5 autres ! Le problème est donc résolu, victoire !
… Vraiment ? Il reste en fait une difficulté. Autant la solution proposée est raisonnablement simple, autant expliquer aux 6 équipes quels matchs elles doivent jouer dans quel ordre pour la réaliser, n’est pas si évident ! Mon frère n’a pas forcément envie de tenir un tableau des matchs, à suivre scrupuleusement…
En réfléchissant à cela, je suis en fait arrivé à une description plus simple de la solution proposée ! Je représente cette fois-ci les équipes et leurs rencontres par un graphe complet à 5 sommets, et non plus 6. En fait je décide de ne plus représenter l’une des équipes — on l’appellera l’équipe 0. Cela n’est pas si artificiel : l’équipe 0 sera amenée à rencontrer les 5 autres. Pour décrire le planning des matchs, il suffit que je puisse indiquer quels autres matchs doivent avoir lieu lorsque l’équipe 0 rencontre chacune des 5 autres équipes. Maintenant, une phase correspond au choix d’une des 5 équipes (celle qui rencontre l’équipe 0), et à un couplage de 2 arêtes entre les 4 autres équipes. Dès lors, on peut proposer les 5 phases suivantes :
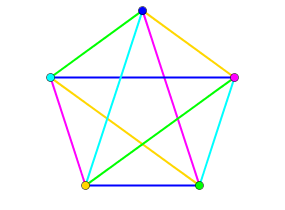
Figure 5
Cette solution a l’avantage d’être particulièrement symétrique et simple à décrire : en effet, chaque phase est obtenue à partir de la première à partir d’une permutation cyclique des 5 équipes. Concrètement, mon frère peut demander à l’équipe 0 de rester sur son demi-terrain, et aux 5 autres de tourner cycliquement sur les 5 demi-terrains restant. Encore plus concrètement, si on a numéroté les demi-terrains ainsi :
0-5
1-4
2-3,
alors l’équipe en 0 y reste, tandis que les autres passent cycliquement en 1, 2, 3, 4, 5. Par ailleurs, cela se généralise aisément au cas de 2n équipes jouant sur n terrains. On peut alors effectuer 2n-1 phases de jeu de sorte que chaque équipe rencontre les 2n-1 autres.
Pour élargir un peu nos propos, remarquons que le problème que nous nous sommes posé est équivalent au problème de planification d’un championnat qui comprendrait 2n équipes et 2n-1 journées (si il n’y a pas de match retour). Je ne connais pas la littérature sur le sujet, mais le problème est certainement bien connu, bien plus profondément que ce que l’on a abordé ici. On trouve d’ailleurs facilement sur internet des planificateurs de championnat, qui créent un planning automatiquement. Ces plannings ont d’ailleurs l’air beaucoup plus désordonnés que celui que j’ai proposé ici. Peut-être cela a-t-il un intérêt pratique dans le cas d’un championnat ?
Ceci dit, je ne suis pas certain que tout soit connu concernant ce problème. Sait-on compter le nombre de solutions ? Sait-on en particulier compter le nombre de solutions vraiment distinctes, c’est-à-dire qui ne peuvent pas être obtenues l’une à partir de l’autre en permutant des équipes et en permutant des journées ? Dans le cas de 6 équipes, comme on l’a vu, il n’y a qu’une seule solution en ce sens.
Enfin, l’intérêt de la solution proposée tient justement à sa simplicité et à la facilité de sa mise en place. Son petit inconvénient, selon moi, est de demander à l’une des équipes de ne pas changer de terrain. Or, nous savons tous que les terrains ne sont pas strictement équivalents (recul pour servir, obstacles environnant, éclairage, etc). Y aurait-il une solution qui remédie en plus à cela, tout en restant simple à mettre en place ? Je n’ai pas de réponse…


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.