
Le prix Nobel de chimie 2011 a été décerné il y a quelques jours au chimiste Daniel Shechtman pour sa découverte des quasi-cristaux. Comme le mentionne le communiqué de presse de la fondation Nobel (en anglais), il y a des mathématiques cachées derrière tout cela.
Daniel Shechtman observa en 1982 un cristal dans lequel « les atomes étaient assemblés dans un modèle qui ne pouvait pas être répété », bousculant la conviction des scientifiques de l’époque selon laquelle l’arrangement des atomes dans un cristal était nécessairement périodique. La forme mathématique d’un quasi-cristal correspond à la notion de « structure quasi-périodique », ou encore « pavages de Penrose », qui ont déjà été évoqués ici.
Un pavage du plan est périodique s’il peut être construit en répétant à l’infini un seul et même motif. Par exemple, on peut toujours paver le plan de façon périodique avec un quadrilatère (voir cet article). C’est sûrement ce que vous avez fait dans votre salle de bains, avec des carrés ou des rectangles.

.

.
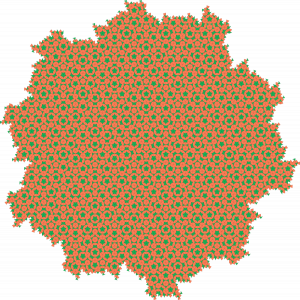
Le mathématicien et physicien Roger Penrose a découvert dans les années 1970 des pavages du plan constitués de deux types seulement de carreaux, et qui ne sont pas périodiques. Mais chacun des motifs qui les composent apparaît régulièrement : on dit que ces pavages sont quasi-périodiques.
.
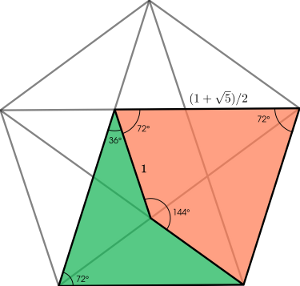
En voici un exemple ci-dessous, avec deux carreaux de base appelés fléchette (en vert) et cerf-volant (en orange), qui peuvent être construits à l’intérieur d’un pentagone régulier.
En attendant de réaliser un pavage de Penrose dans votre salle de bains, vous pouvez la décorer avec ce poster.
Lors de la fête de la science, il sera aussi possible, à Caen et à Rouen, de construire votre propre pavage à partir de fléchettes et cerfs-volants.
.
Crédits images
Toutes les images appartiennent aux auteurs.



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.