
Ce billet fait partie d’une série sur les « Success stories » européennes liant Mathématiques et Industrie. Ces histoires ont été recueillies dans le cadre du projet intitulé Forward Look « Mathematics and Industry » coordonné scientifiquement par le Comité de Mathématiques Appliquées de l’EMS et financé par l’ESF. Nous les remercions, ainsi que les auteurs pour nous avoir autorisés à traduire ces textes en français. La traduction a été réalisée par Paul Vigneaux.
Auteurs de la version originale : M.A. Peletier et A. Hlod
Résumé
En utilisant la modélisation mathématique, l’analyse et l’analyse numérique du modèle mis au point, nous avons décrit puis validé expérimentalement les caractéristiques du procédé de filage rotatif. Le modèle mathématique permet de mieux comprendre le procédé, au point de suggérer une manière de produire des fibres arbitrairement longues.

Photos du dispositif expérimental.
L’objectif
Le filage rotatif est un procédé de production de fibres aramide solides et résistantes à la température. Ces fibres ont une large gamme d’applications dans l’industrie automobile, les équipements et vêtements de protection, les matériaux composites ou encore les produits type tendeurs linéaires. Cependant, en l’état actuel de la technologie, seules de courtes fibres peuvent être obtenues, alors que la capacité à manufacturer des fibres arbitrairement longues améliorerait significativement la création des produits. On y gagnerait en efficacité de l’outillage de l’unité de production complète.
Il est très difficile et coûteux de réaliser des études expérimentales de ce procédé. Il s’agit donc d’un bon candidat pour une étude mathématique.
Mise en œuvre de l’initiative
L’entreprise Teijin Aramid a proposé le problème du filage rotatif à la communauté mathématique lors du 48me « Groupe européen d’étude mathématique avec l’Industrie » 1NdT : en anglais, les Study Group Mathematics with Industry ; on pourra consulter cette page pour plus d’informations., à Delft, Pays-Bas, en 2004. Seules des avancées partielles avaient pu être réalisées durant ce workshop d’une semaine et ce problème est devenu le sujet de thèse d’Andriy Hlod, à l’Université de Technologie d’Eindhoven. L’entreprise faisait pleinement partie du processus de recherche en fournissant non seulement des commentaires et des retours mais aussi des dispositifs expérimentaux.
Modélisation mathématique et analyse
Le procédé de filage rotatif est modélisé par un jet d’un fluide visqueux subissant des forces centrifuges et de Coriolis et frappant une paroi mobile. Le jet est décrit à l’aide d’un modèle de ressorts (analogues aux ressorts élastiques) qui contient les effets inertiels et de viscosité élongationnelle. Le jet stationnaire, qui est l’écoulement opératoire recherché en priorité, est décrit à l’aide d’un système d’équations différentielles ordinaires avec une surface libre.
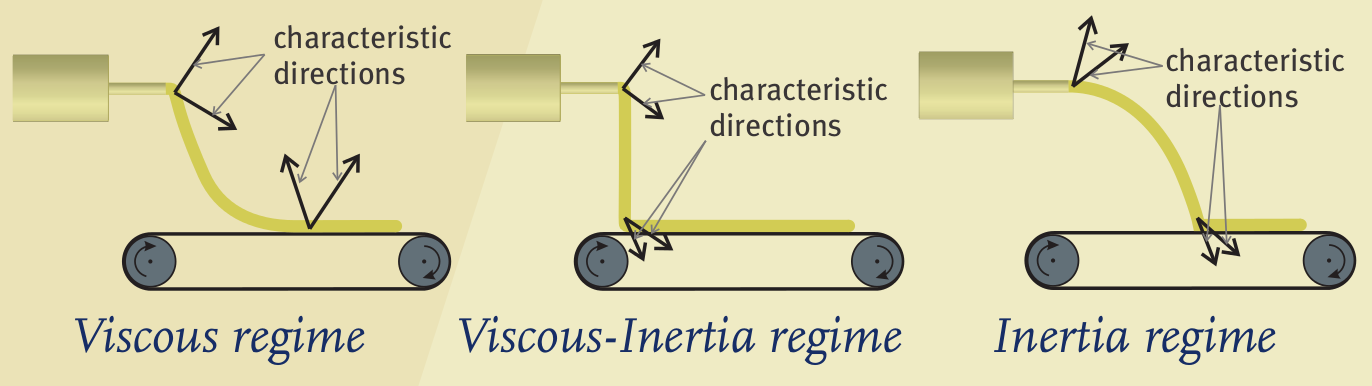
Les 3 régimes d’écoulement du jet tombant sur une surface mobile sont caractérisés par l’effet prépondérant dans le transfert de moment : régime visqueux, visqueux-inertiel ou inertiel. Chaque caractéristique rentrante (indiquée par les flèches) induit une condition aux limites pour la position et l’angle.
Pour simplifier le problème, nous avons étudié le modèle de jet dans une situation sans rotation où le jet tombe sous l’effet de la gravité sur une surface mobile. Un point crucial était le choix de la condition aux limites sur cette surface ; la découverte clé a été que le problème dynamique est de type hyperbolique-parabolique et que la condition aux limites doit être choisie en fonction du comportement des directions des caractéristiques de la composante hyperbolique. Physiquement, le choix de cette condition aux limites reflète l’effet dominant dans le transfert de moment au travers d’une section transverse. Cette analyse a montré l’existence de trois régimes d’écoulement dont la dépendance aux paramètres du procédé est contre-intuitive. Un point important est que les expériences menées par le Dr Hlod, avec l’aide de Teijin Aramid, ont confirmé cette dépendance non triviale et donnent ainsi de manière indépendante une confirmation de ce choix de conditions aux limites.
Nous avons ensuite appliqué cette théorie du jet au modèle de filage rotatif. Cela nous a permis de caractériser l’espace des paramètres et d’obtenir les régions de paramètres où le filage est possible. De plus, nous avons développé un schéma numérique pour le problème dynamique.
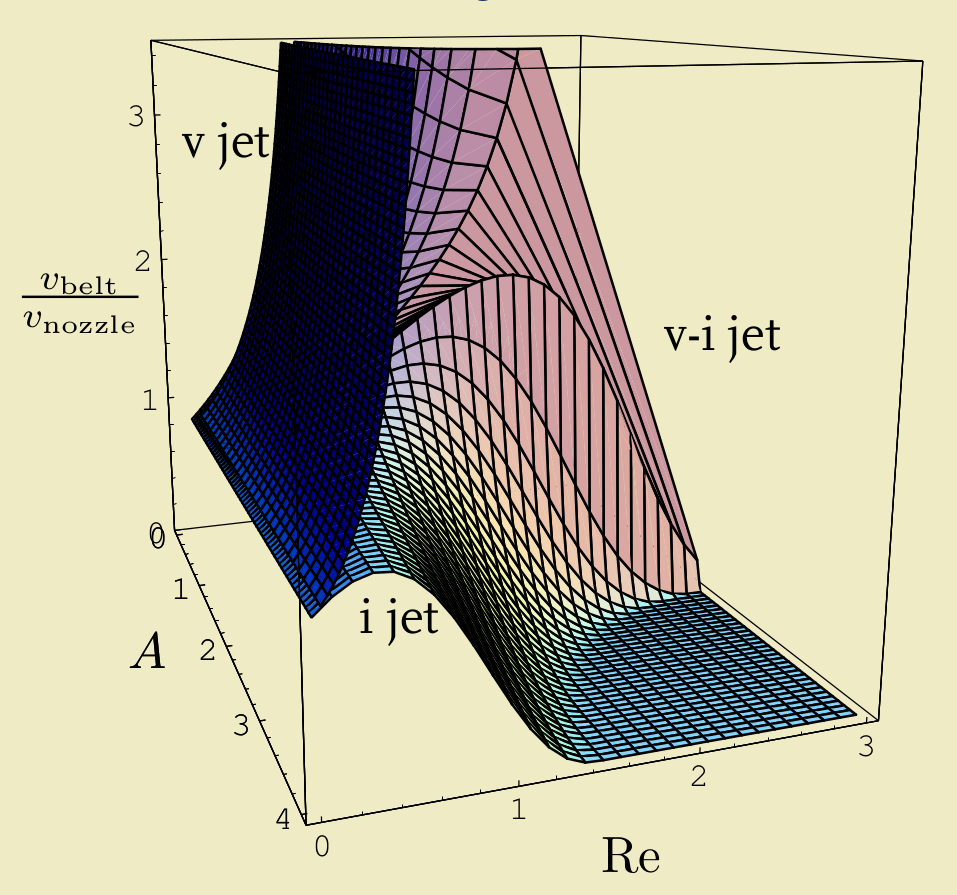
Espace des paramètres et régions pour les 3 régimes.
Résultats
Le partenaire industriel a pu obtenir des indications sur les causes de la rupture de la fibre lors de sa production par filage rotatif, ce qui a initié des recherches expérimentales plus approfondies. La thèse de doctorat d’Andriy Hlod a été recompensée par le Prix Anile-ECMI pour les Mathématiques dans l’Industrie lors de l’ECMI 2010 2NdT : la Conférence Européenne sur les Mathématiques pour l’Industrie. Elle s’est tenue à Wuppertal en Allemagne, en juillet 2010..
Contact
Prof. M.A. Peletier (m.a.peletier@tue.nl) et Dr. A.Hlod (avhlod@gmail.com). Eindhoven University of Technology, Center for Analysis, Scientific computing, and Applications. Eindhoven. Pays-Bas.
Partenaire industriel
Teijin Aramid
Post-scriptum
Pour plus d’informations sur ces « Success Stories » et quelques éclairages sémantiques sur certains termes en italique, on pourra consulter ce billet.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.