
Ce billet fait partie d’une série sur les « Success stories » européennes liant Mathématiques et Industrie. Ces histoires ont été recueillies dans le cadre du projet intitulé Forward Look « Mathematics and Industry » coordonné scientifiquement par le Comité de Mathématiques Appliquées de l’EMS et financé par l’ESF. Nous les remercions, ainsi que les auteurs pour nous avoir autorisés à traduire ces textes en français. La traduction a été réalisée par Paul Vigneaux.
Auteurs de la version originale : Stefano Fanfani et Alessandro Speranza
Résumé
Ce projet consiste en la simulation de la décharge luminescente au cours d’un dépôt physique en phase vapeur par pulvérisation cathodique (plasma PVD) à basse pression, utilisé pour des applications industrielles [1]. Les chercheurs d’\(I^2 T^3\) (Industrial Innovation Through Technological Transfer, Florence, Italie), en collaboration avec le Département de Mathématiques de l’Université de Florence, ont développé un modèle pour décrire le plasma dans une telle situation.
L’objectif
Galileo Vacuum Systems srl (GVS) est une entreprise de pointe dans la production d’installations industrielles pour les processus de PVD tels que l’enduction de métaux sur des films plastiques, d’aluminium sur des phares de voitures, etc. GVS avait déjà des collaborations avec \(I^2 T^3\) et des discussions préliminaires sur une nouvelle approche scientifique pour innover sur ce produit étaient en cours. Dans le cas présent, à l’initiative des principaux clients internationaux de GVS, il a été demandé de décrire les effets des paramètres de contrôle prépondérants (comme la pression du plasma ou la géométrie de la chambre de production) sur la qualité finale des produits [2]. Il fallait une approche plus systématique et scientifique pour décrire le processus de conception de nouvelles machines, si possible à l’aide du développement de modèles mathématiques simplifiés du procédé industriel et d’analyses expérimentales.
Mise en œuvre de l’initiative
Au cours de ce projet d’un an, des modèles mathématiques et des simulations numériques ont été réalisés. La collaboration a été co-financée par la Région Toscane dans le cadre de fonds dédiés à l’introduction de produits et procédés innovants dans les entreprises locales.
Le problème
Le modèle est centré sur la prédiction des caractéristiques principales du plasma, créé au sein de la machine par un champ électrique de fort voltage (environ 2000kV). Le procédé industriel sous-jacent (plasma PVD) est décomposé en 3 étapes principales :
- le vide (10\(^{-3}\) mbar) est fait au sein de la chambre ;
- un champ électrique important est appliqué à des électrodes situées dans la chambre et une décharge luminescente est produite, ce qui génère un plasma ;
- un monomère est injecté dans la chambre et polymérise au contact du plasma : un film de polymère se dépose ensuite sur le substrat en plastique que l’on veut enduire, placé préalablement au sein de la chambre.
Le projet s’est concentré plus particulièrement sur la modélisation de la deuxième étape.

Le dispositif industriel (avec l’aimable autorisation de GVS srl) et l’une des géométries utilisées par le modèle pour représenter la chambre où se fait l’enduction par PVD.
Le modèle mathématique est composé d’une équation de conservation de la masse, couplée à un modèle de dérive-diffusion pour la conservation du moment. Tous les effets électriques transitoires ont été négligés et une solution stationnaire a été déterminée. Les conditions aux limites associées à ces équations s’avèrent être assez complexes car, même en négligeant les termes à l’ordre 2, elles dépendent de la solution elle-même. Cela induit un couplage fortement non linéaire qu’il est difficile de résoudre. De plus, dans cette approche, certains paramètres doivent être déterminés expérimentalement et sont inclus dans le modèle. Notons qu’à l’opposé, dans les approches classiques, ces paramètres sont généralement estimés pour des situations très simples et idéalisées.
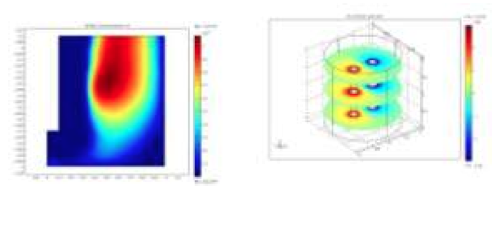
Le travail réalisé permet de simuler notamment le potentiel électrique, la densité d’ions et d’électrons pour différentes géométries de la chambre. Gauche : coupe verticale avec hypothèse de symétrie cylindrique (Cathode au centre et anode en périphérie). Droite : coupes horizontales le long de l’axe de la chambre à deux électrodes (Comme à la Figure 1. La symétrie cylindrique de l’intérieur de la chambre est alors brisée, par rapport à la figure de gauche où il n’y a qu’une électrode à l’intérieur).
Résultats
Au cours de ce projet, l’entreprise a lancé un nouveau processus d’innovation visant à renouveler l’ensemble de la conception et de la production de ses machines industrielles. \(I^2 T^3\) a développé un savoir faire nouveau et pointu sur la modélisation mathématique du dépôt physique en phase vapeur par pulvérisation cathodique.
Contact
Ing. Stefano Fanfani (sfanfani1@alice.it). Galileo Vacuum Systems srl, Prato. http://www.galileovacuum.com

.
Dr. Alessandro Speranza (alessandro.speranza@i2t3.unifi.it). Innovazione Industriale Tramite Trasferimento Tecnologico, Université de Florence. http://www.i2t3.unifi.it

.
Post-scriptum
Pour plus d’informations sur ces « Success Stories » et quelques éclairages sémantiques sur certains termes en italique, on pourra consulter ce billet.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.