Les mathématiques au collège

Beaucoup d’élèves en sont encore demandeurs, et même passionnés !

Dans le cadre de nos activités à la Cité des Géométries, nous sommes intervenus à trois reprises dans l’une des classes de Madame Nathalie Lienard, professeur de mathématiques au Collège Alfred Jennepin à Cousolre. Quelques jours avant notre première intervention, Nathalie nous a fait part de l’intention des élèves de nous soumettre quelques questions qui les turlupinent, avant d’aborder le thème de travail que nous allions leur proposer ! L’initiative était la bienvenue et, bien entendu, nous avons accepté le jeu. De plus en plus, nous souhaitons et apprécions ce genre de requête dans les établissements secondaires, et surtout lorsque les élèves eux-mêmes suggèrent le contenu et initient le débat. Ça permet de véritables échanges, plus bénéfiques que des exposés à sens unique, au bout desquels il n’y a aucun moyen de savoir ce qui est véritablement passé et resté dans les têtes. Leurs questions portaient sur un sujet rarement traité (de quelque « façon détaillée » on va dire) dans les programmes du secondaire : l’infini.

De jeunes collégiens confrontés à la présence de l’infini en mathématiques ! Comme par exemple l’infinité des nombres naturels, des points sur une droite, de ceux d’un segment aussi petit que l’on veut, et bien d’autres… Ils sentent que les difficultés ne sont plus du même ordre quand ils ont affaire à une partie d’un ensemble infini qu’à celle d’un ensemble fini. On a l’habitude de dire que dans un ensemble fini, le tout est plus grand que la partie. Quand les élèves découvrent que ceci n’est plus « vrai » dans un ensemble infini, ils sont tout simplement perturbés ! Ceux que nous avons eus à ces « séances-échanges » titubaient à formuler leurs questions : avec les outils fournis dans l’enseignement secondaire actuel, ils ont du mal à comprendre qu’il y a des infinis de plusieurs sortes, et que les modes de penser auxquels ils sont habitués ne permettent pas de distinguer.

Ceci dit, les questions fusèrent tout de même ! Les élèves se demandaient par exemple si, dans un cercle, l’infinité de ses rayons est la même que celle de ses diamètres. Mais aussi, si deux segments de longueurs différentes contiennent la même infinité de points. Nous avons pu leur prouver, tant bien que mal, qu’il s’agit de la « même infinité ». La preuve, axée bien sûr (comme tout le monde le sait) sur l’existence de bijections (qu’on sait même dessiner) entre les différents ensembles en jeu, les a convaincus et drôlement enchantés ! Toutefois, la perception qu’ils ont réellement eue et gardée de la notion d’infinité est celle d’infinité dénombrable : c’est infini parce qu’on numérote les éléments et qu’on peut le faire tant qu’il le faut et sans jamais être arrêté ! Mais cette façon de faire est aussi celle de tout le monde dans la vie courante (il n’y a presque que le mathématicien qui va vers le continu).

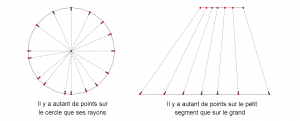
Au passage, nous n’avons pas manqué de parler de certains paradoxes en rapport avec le thème. Comme l’étymologie le suggère, un paradoxe est une idée « contraire à l’opinion commune ». Il n’est pas évident d’ouvrir de telles discussions au collège : les paradoxes sont plutôt traités au lycée et même, pas toujours en cours de philosophie. Ceci dit, le paradoxe est un moyen très puissant pour stimuler l’imagination et la curiosité des élèves, surtout lorsqu’ils se sentent prêts à « aller dedans ». Nous nous y sommes aventurés quand même en en proposant quelques-uns, devenus célèbres depuis que Hilbert les a énoncés. (Nous nous sommes limités à l’infinité dénombrable que nous avons pris soin de leur expliquer.)

Après quelques réponses, un peu fantaisistes du type « On vire Jean-Pierre Biftèque de sa chambre et on y met Pauline Merguèze » laissant éclater des rires, nous nous sommes mis avec un peu plus de sérieux sur la question. Une vague idée a été proposée par l’un des élèves. Elle était bonne et, ensemble, nous l’avons précisée et menée à terme en montrant bien que l’hypothèse « le nombre de chambres est infini » joue un rôle clé dans l’existence de la solution. Les élèves furent subjugués et en demandèrent plus. Nous leur servîmes alors un deuxième paradoxe, qui n’était d’ailleurs qu’une suite naturelle du premier.

Mais le temps nous a manqué et nous n’avons pu continuer la discussion devenue de plus en plus passionnante aussi bien pour les élèves que pour nous. Nous leur avons proposé de poursuivre la réflexion chez eux, ce qu’ils ont accepté bien volontiers. La semaine qui suivit, un autre élève est arrivé avec presque la solution en poche. La séance a continué d’une manière analogue mais sur d’autres sujets. La troisième portait sur de la géométrie et, surtout, sur une sensibilisation à l’intérêt du « regard » dans la résolution de certains problèmes en géométrie plane élémentaire. C’était super !

Ces rencontres ont permis aux élèves d’ouvrir leurs horizons et, à nous, d’affiner nos capacités à adapter nos discours à des thématiques fines et un peu plus complexes que celles d’habitude.

Ce type d’intervention est une gymnastique plaisante à laquelle nous convions les universitaires qui ne sont souvent impliqués, en dehors de leur enseignement, que dans leurs travaux de recherche individuels. Ils devraient se décloisonner, donner un peu de leur temps et aller voir ce qui se passe du côté des lycées et collèges. C’est de la recherche tout aussi noble et enrichissante !

Qu’en pensez-vous chères lectrices et chers lecteurs ?