
Bhāvanā est un journal papier et un site internet indien né en 2017 qui, à l’instar d’Images des mathématiques (IdM), a pour raison d’être de donner un aperçu accessible au plus grand nombre du monde de la recherche actuelle en mathématiques.
IdM se réjouit de cette belle initiative et s’est proposé, avec l’accord des éditeurs de Bhāvanā, de traduire et de rediffuser certains de leurs articles. L’article ci-dessous est paru en janvier 2018, vous pouvez lire l’original ici.
Enrico Castelnuovo est un écrivain italien et le père du géomètre algébriste Guido Castelnuovo. Sa nouvelle intitulée « Teorema di Pitagora » (« Théorème de Pythagore ») est parue initialement en italien en 1886 dans son recueil de nouvelles Sorrisi e lagrime (Sourires et larmes).

Enrico Castelnuovo Portrait d’Enrico Castelnuovo par Francesco Scattola, entre 1900 et 1924

Guido Castelnuovo
Portrait de Guido Castelnuovo jeune
Guido Castelnuovo, les mathématiques et leur enseignement
Né à Venise en 1865, Guido Castelnuovo est l’un des plus anciens et des plus fameux membres de l’école de géométrie algébrique italienne. Son intérêt pour la géométrie a été instillé par Veronese, qui était son professeur à Padoue. Castelnuovo y reçoit son diplôme puis passe presque toute sa carrière académique dans diverses universités en Italie. Il travaille également en collaboration étroite avec les meilleurs mathématiciens de son temps tels que Corrado Segre, Luigi Cremona, Alexander von Brill et Max Noether.
Au début de sa carrière, Castelnuovo envoie un de ses articles à Corrado Segre, un des chefs de file de la géométrie de l’époque. La réponse rapide et soigneusement commentée de Segre lui offre une surprise agréable. Quand il exprime sa gratitude, Segre aurait répondu : « C’est une mauvaise habitude, même si elle est répandue, de vanter des articles sans les avoir lus. Au contraire, j’ai l’habitude de lire tous les papiers que je reçois et d’envoyer mes remarques aux auteurs : je fais aux autres ce que je voudrais qu’ils me fassent. » C’est une idée répandue que l’école italienne de géométrie algébrique s’est hissée au premier plan pendant les années 1887-1891 que Castelnuovo a passées à Turin. Il discutait de la géométrie des courbes algébriques avec son mentor et collaborateur Segre pendant de longues promenades sous les arcades de la via Po à Turin.
Castelnuovo est un orateur invité au congrès international des mathématiciens à Bologne en 1928 et, d’après le titre de sa conférence, La geometria algebrica a la scuola italiana (La géométrie algébrique dans l’école italienne), on peut déduire son profond intérêt pour la recherche et l’enseignement. Conformément à sa propre philosophie sur la façon dont les mathématiques devraient être enseignées, il divisait généralement son cours en deux parties, la première offrant une vision générale des mathématiques alors que la deuxième était plus spécialisée. « [L]a raison pour la division, écrit-il, est que d’un côté il faut avoir de la culture générale et de l’autre, il faut avoir une connaissance approfondie d’un domaine particulier. »
Parmi ses principaux étudiants, Oscar Zariski est un de ceux qui ont eu un impact durable sur l’avènement de la géométrie algébrique comme une discipline mathématique majeure au vingtième siècle. C’est une histoire intéressante et bien connue, racontée par Zariski lui-même, que celle de son examen par Castelnuovo sur plusieurs domaines de mathématiques, à son insu, pendant une promenade de trois heures dans Rome, à la fin de laquelle Castenuovo a annoncé à Zariski qu’il le prenait comme étudiant.
Les intérêts de Castelnuovo se sont plus tard tournés vers la théorie des probabilités et la théorie de la relativité – il a même écrit un livre intitulé Calcolo delle probabilità (Calcul des probabilités) en 1919 et un texte sur la relativité en 1923. Il s’est également intéressé à l’histoire des mathématiques. En 1911-1914, Castelnuovo est le président de « Mathesis », une association d’enseignants de mathématiques fondée en 1895-1896, et fait des contributions décisives pour mettre en place les programmes de mathématiques du lycée en Italie. La citation suivante témoigne de sa vision remarquable :
En fin de compte, aucune école n’est efficace à moins d’être capable d’impliquer une intelligence moyenne, à moins d’être capable de former une démocratie éduquée, qui est la base de toute nation moderne. Étudier les moyens par lesquels l’éducation peut être diffusée, même s’il faut sacrifier un peu de profondeur, voilà le problème que nous sommes appelés à résoudre.
Ses mots emphatiques sur l’éducation scolaire restent pertinents aujourd’hui :
L’école secondaire ne devrait pas tant apporter des connaissances à leurs élèves que le désir et le besoin de connaissances. Elle ne doit pas chercher à fournir une connaissance encyclopédique de tout mais peut seulement offrir une idée claire, même si elle est nécessairement très limitée, des principaux problèmes étudiés par chaque branche du savoir, et certaines des méthodes qui ont été employées pour les aborder. Elle ne devrait pas s’effrayer de sacrifier la profondeur à la largeur des idées. Bien sûr, ce type d’enseignement ne sera pas suffisant pour donner des lycéens une préparation spécifique à l’une ou l’autre des facultés de l’université. Cependant, ce n’est pas le but de l’école secondaire. Elle sert simplement à fournir aux étudiants la capacité de se lancer dans des études plus avancées.
Classe 3A du lycée Foscarini (1er juin 1882)
Photographie (datée du 1er juin 1882) d’un groupe d’étudiants et de professeurs de la classe 3A du lycée d’État « Marco Foscarini ». Le quatrième étudiant debout en partant de la droite est Guido Castelnuovo (le troisième de la rangée du milieu, avec la veste sombre derrière le professeur moustachu), fils d’Enrico Castelnuovo.
Antonio Sorgato / Università Ca’Foscari Venezia Archivio Storico – Istituto Matematico Guido Castelnuovo – sacherfire via Flickr.
Ailleurs, il note :
Il est souvent préférable de procéder par approximations successives, où chaque étape est évaluée en rapport avec des faits réels, pour séparer le vrai du faux petit à petit, plutôt que de se reposer sur une logique impeccable étanchement séparée du monde extérieur. La façon dont les mathématiques sont enseignées dans les écoles aujourd’hui fuit à tort la première approche et abandonne par conséquent la seule façon de penser qui est commune à la plupart des gens. L’accent mis sur la démonstration de ce qui est intuitivement évident au moyen de la logique provoque doublement des dégâts, en sapant le raisonnement, qui a une fonction différente, et l’intuition, en niant sa valeur immense. On peut toujours dire que l’intuition peut mener à des erreurs ; peut-être. Mais l’intuition donne aussi le chemin principal, sinon le seul, vers la découverte de la vérité. Devrions-nous vraiment abandonner la vérité pour éviter de commettre des erreurs ? Si nous voulons bien enlever de la géométrie toute une série de gymnastiques mentales dénuées de tout propos, nous serons peut-être capables, je crois, d’atteindre deux buts qui semblent incompatibles à première vue. Nous pourrons élever la valeur pédagogique des mathématiques et, en même temps, nourrir plusieurs facultés mentales, au lieu de tout sacrifier à une seule d’entre elles. Simultanément, nous rendrons les mathématiques amusantes et accessibles à tout le monde, et nous vaincrons enfin le préjugé que les éléments mêmes de cette discipline ne conviennent qu’à un petit nombre d’esprits choisis.
Guido Casetlnuovo a joué un rôle essentiel pour donner à l’université de Rome une forte réputation, et de façon pertinente, le département de mathématiques porte désormais son nom : Istituto Matematico Guido Castelnuovo.
Il a été profondément influencé par la vie et l’œuvre de son père Enrico Castelnuovo, célèbre auteur italien. Dans la nouvelle ci-dessous (traduite en français), le père Enrico Castelnuovo raconte très clairement sa rencontre ignominieuse avec le célèbre théorème de Pythagore, jusqu’au retour inattendu du spectre de cet événement peu mémorable plusieurs années après dans le cahier de son fils. Bien que l’histoire elle-même comporte un humour délicieux, elle reflète un sentiment typique de nombreuses personnes qui préfèrent éviter tout contact avec les mathématiques. Tout de même, elle met en avant de façon amusante le message selon lequel la créativité mathématique n’est pas nécessairement une affaire héréditaire.
« Le théorème de Pythagore »
— Le théorème de Pythagore ! dit avec un certain air de raillerie le professeur Roveni, en dépliant un petit papier que j’avais tiré très délicatement d’une urne posée sur le bureau. Puis il montra le papier au Commissaire du gouvernement qui se tenait à côté de lui et lui susurra quelques mots à l’oreille. Finalement, il me remit le morceau de papier pour que je puisse y lire de mes propres yeux l’énoncé de la question.
— Passez au tableau, ajouta le professeur en se frottant légèrement les mains.
Le candidat qui m’avait précédé dans l’épreuve et qui s’en était tiré tant bien que mal sortit de l’école sur la pointe des pieds et, en ouvrant la porte, laissa passer dans la salle une longue bande de lumière. Dans cette bande lumineuse qui vacillait sur le mur et sur le sol, j’eus la satisfaction de voir mon ombre.
La porte se referma et une demi-obscurité envahit à nouveau la classe. Il faut dire que c’était une journée étouffante d’août et que les gros rideaux de toile bleue étaient un faible remède contre les rayons ardents du soleil, si bien que les fenêtres étaient fermées. Le peu de lumière qui restait allait se concentrer sur le bureau et sur le tableau. Pour éclairer ma déroute il y en avait toujours assez.
— Allez au tableau et tracez la figure, répéta le professeur Roveni qui s’était aperçu de mes hésitations.
Tracer la figure était la seule chose que je savais, pour ce faire je pris un morceau de craie et je me mis consciencieusement à l’œuvre. Je n’étais pas pressé ; plus je prenais de temps pour cette partie graphique, moins il en restait pour la partie orale.
Mais le professeur n’était pas homme à se laisser berner par mon artifice innocent.
— Dépêchez-vous, me dit-il. Ce n’est quand même pas la Madone de Raphaël que vous devez me faire.
Il fallut en finir.
— Mettez les lettres maintenant… Vite, ne faites pas un essai de calligraphie. Pourquoi est-ce que vous effacez ce G ?
— Pour ne pas le confondre avec le C que j’ai fait avant. Je le remplace par un H.
— Quelle délicate pensée ! observa Roveni avec son ironie habituelle. Vous avez fini ?
-

Face au tableau
— Oui Monsieur.
Et j’ajoutai pour moi seul :
— Malheureusement.
— Allez, pourquoi est-ce que vous restez ensorcelé, ici ? Énoncez le théorème.
Ici commençait la partie douloureuse. Les mots mêmes de la question avaient disparu de mon esprit.
— Dans un triangle, commençai-je en balbutiant.
— Continuez.
Je pris courage et je dis ce que je savais :
— Dans un triangle… le carré de l’hypoténuse est égal aux carrés des deux autres côtés.
— Dans un triangle quelconque ?
— Non, non, suggéra une âme pieuse derrière moi.
— Non, Monsieur, dis-je.
— Expliquez-vous ; dans quel triangle ?
— Un triangle rectangle, susurra la même voix.
— Silence, là derrière ! hurla le professeur.
Puis il continua en se retournant vers moi :
— Alors, d’après vous, ce grand carré est égal à chacun de ces petits carrés ? Mince, c’était absurde. Mais j’eus une bonne inspiration.
— Non Monsieur : à tous les deux ensemble.
— À la somme, donc ; dites à la somme, et dites équivalent, pas égal. Maintenant, démontrez-le. Je transpirais mais malgré la chaleur tropicale, ma sueur était gelée ; je regardais hébété le triangle rectangle, le carré de l’hypoténuse et des deux rejetons, je passais la craie d’une main à l’autre et je ne disais rien pour la raison imparable que je n’avais rien à dire. Personne ne suggérait plus rien. Dans la classe, on aurait entendu voler une mouche. Le professeur Roveni fixait au-dessus de moi ses petits yeux gris dans lesquels brillait une joie maligne, le Commissaire du gouvernement prenait quelques notes sur une feuille de papier. Tout à coup ce respectable personnage se racla la gorge et le professeur Roveni dit avec force insinuation :
— Eh bien ?
Je ne répondis pas.
Au lieu de me renvoyer directement, le professeur voulut imiter le chat qui joue avec la souris avant de la dévorer.
— Comment ? ajouta-t-il. Peut-être que vous cherchez une solution nouvelle. Je ne dis pas que vous ne pouvez pas la trouver mais nous autres, nous nous contenterons d’une des anciennes. Allons. Ne vous rappelez pas qu’il faut prolonger les deux côtés DE et MF jusqu’à ce qu’ils se croisent ? Prolongez-les, courage !
Je fis machinalement ce qu’il m’avait indiqué. La figure prenait des proportions géantes et me pesait sur l’estomac comme le poids d’un cyclope.
— Mettez une lettre au point d’intersection, un N. Voilà. Et maintenant ? Je restais muet.
— Il ne vous semble pas nécessaire d’abaisser une droite de N par A jusqu’à la base du carré BHIC ?
-
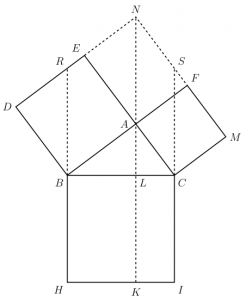
Figure
À moi, rien ne me paraissait bien nécessaire : j’obéis néanmoins.
— Ensuite, vous devrez bien prolonger les deux côtés BH et IC. Ouf ! Je n’en pouvais plus.
— Maintenant, reprit le professeur, même un enfant de deux ans sait faire la démonstration. Vous n’avez rien à observer autour des deux triangles BAC et NAF ?
Puisqu’en me taisant, je ne faisais que prolonger mon supplice, je répondis laconiquement :
— Rien.
— Autrement dit, vous ne savez vraiment rien ?
— Il me semble que vous devez vous en être un peu aperçu, observai-je avec un calme digne de Socrate.
— Mais bravo, vraiment bravo : vous le prenez sur ce ton ? Et vous ne savez même pas que le théorème de Pythagore est aussi appelé le pont-aux-ânes parce que seuls les ânes ne le passent pas ?… Allez-vous-en alors. Vous comprenez bien que vous avez échoué à l’examen. Comme ça, vous apprendrez à lire le Don Quichotte ou à dessiner des chats pendant mes cours.
Le Commissaire du gouvernement prisa une pincée de tabac ; je déposai la craie et la brosse et je sortis majestueusement de la salle sous les rires étouffés de mes condisciples.
Trois ou quatre camarades qui avaient déjà passé l’examen avec un succès à peine plus brillant que le mien m’attendaient dehors.
— C’est un fiasco, alors ?
— Un super fiasco, répondis-je en me pavanant avec un noble orgueil. Et j’ajoutai : Je l’ai toujours dit, que la mathématique n’est faite que pour les bourrins.
— C’est clair, s’exclama un de mes émules.
— Et quel sujet tu as tiré ? demanda un autre.
— Le théorème de Pythagore. Ou qu’est-ce que ça peut me faire que le carré de l’hypoténuse soit ou ne soit pas égal à la somme des carrés des deux autres côtés ?
— Mais ça ne peut rien te faire, ni à toi, ni à moi, ni à personne au monde, s’empressa un troisième avec la pétulance d’un ignorant de quatorze ans. Et puis, s’il est égal, pourquoi est-ce qu’ils ont besoin de se l’entendre répéter ? Et sinon, pourquoi ils nous embêtent ?
— Croyez-le pourtant, mes amis, dis-je en reprenant l’initiative dans la discussion avec la prosopopée d’un homme de grande expérience, croyez-le pourtant. Tout le système d’éducation est faussé, et tant que les Allemands seront ici, il le sera toujours.
Persuadés que notre échec était une protestation contre la domination étrangère et la preuve d’un esprit vif et original, nous nous dirigeons vers la maison, où pour ma part, je le confesse, j’ai senti refroidir quelque peu l’enthousiasme initial.
Cet examen raté de façon si ignominieuse eut une grande influence sur mon avenir. Puisqu’il n’y avait pas moyen que je comprisse les mathématiques, il fut décidé ce jour-là en famille de me faire interrompre le cours technique. D’autre part, les conditions familiales ne me permettaient pas de recommencer mes études au lycée. Il fallait absolument que j’entrasse dans la vie active, que je pusse gagner rapidement quelque argent.
C’était le parti le plus raisonnable qui pouvait être pris et je n’avais aucun droit de m’y opposer. Toutefois, je dois dire que j’en fus profondément attristé. Mon aversion des mathématiques ne s’étendait pas aux autres matières enseignées, dans lesquelles je faisais plutôt des progrès discrets. Et puis, j’aimais l’école. J’aimais ses cloîtres sévères que nous autres garçons emplissions de vie et de gaîté, j’aimais ses bancs de bois entaillés par nos canifs, j’aimais même son tableau noir qui avait été le témoin de ma défaite irréparable.
Et je m’en prenais au théorème de Pythagore. Avec une autre question, qui sait ? j’aurais pu mettre quelques phrases bout à bout, j’aurais pu m’en sortir de justesse, comme les années précédentes. Mais je devais justement tomber sur celui-là !
J’en rêvai toute la nuit. Je voyais toujours ce terrible carré avec son triangle collé au-dessus, d’où naissaient deux carrés plus petits, tournant l’un à droite, l’autre à gauche. Ensuite, je voyais un fatras de lignes, une grande confusion de lettres majuscules et j’entendais me marteler dans la tête : BAC=NAF ; RNAB=DEAB.
Il fallut un bon moment avant que je ne fusse libéré de ce cauchemar, avant que Pythagore et ses trois carrés me sortissent de l’esprit. À la longue, cependant, le temps, qui de son éponge efface tant de choses du livre de la mémoire, y avait effacé aussi celle-ci, quand il y a quelques semaines la figure de mauvais augure m’apparut inopinément dans un cahier de mon fils.
— Cette malédiction se transmet donc aussi à mes descendants ! m’exclamai-je. Pauvre garçon ! Si le théorème de Pythagore lui était aussi fatal, comme il me le fut ?
Je voulus l’interroger à son retour de l’école.
— Alors, commençai-je avec gravité, vous êtes arrivés avec votre géométrie au théorème de Pythagore ?
— Oui, Papa, me répondit-il avec désinvolture.
— Théorème difficile, ajoutai-je en hochant la tête.
-

Retour inattendu du théorème
— Tu trouves ? demanda-t-il en souriant.
— Tu voudrais faire le fanfaron et me faire croire qu’il te semble facile ?
— Sûr qu’il me semble facile.
— Je serais curieux de voir un peu la preuve, m’échappa-t-il involontairement. C’est inutile, je ne supporte pas les vantardises.
— Tout de suite, dit le crâne freluquet. Et aux paroles succédèrent les actes. Il prit une feuille de papier et un crayon et traça rapidement la figure cabalistique.
— Quant à la démonstration, reprit-il, il n’y a que l’embarras du choix. Pour toi, ça ne te fait rien, l’une ou l’autre ?
— Oui, répondis-je machinalement. Et en effet, ça ne pouvait pas me faire plus que rien. Même s’il y avait eu cent démonstrations, j’étais sûr que je n’en aurais compris aucune.
— Alors, choisissons celle-là, qui est plus courante, poursuivit mon mathématicien.
Ceci dit, il abaissa et prolongea les lignes que le professeur Roveni de bonne mémoire m’avait fait abaisser et prolonger vingt-sept ans avant, et avec le ton de la plus sincère conviction, il s’apprêta à me prouver que le triangle BAC était égal au triangle NAF et que le losange RNAB était comme un fruit coupé en deux, le carré DEAB, et que tant d’autres choses étaient égales entre elles, d’où il résultait comme conséquence naturelle que le carré BHIC était équivalent à la somme des deux carrés CAFM et DEAB.
— Et maintenant, dit mon fils quand il eut terminé son verbiage, nous pouvons, si tu veux, arriver à la même conclusion par un autre chemin.
— Par pitié ! m’exclamai-je atterré. Maintenant que nous sommes arrivés, reposons-nous des fatigues du voyage.
— Mais je ne suis pas du tout fatigué.
Même pas fatigué ! Ce garçon était donc un Newton en herbe ! Et on discute du principe d’hérédité !
— Je suppose qu’en mathématiques, tu seras le premier de la classe, lui dis-je, sous l’effet d’une certaine peur révérencielle.
— Non, non, répondit-il. Il y en a deux qui sont meilleurs que moi. Et puis, tu sais très bien qu’à part les ânes, le théorème de Pythagore, tout le monde le comprend.
À l’exception des ânes ! Après vingt-sept ans, j’entendais dans la bouche de mon fils les mêmes paroles que j’avais entendues du professeur Roveni le jour mémorable de mon examen. Et cette fois, il y avait en plus la féroce ironie du « tu sais très bien ».
Je voulus sauver les apparences et j’ajoutai dans une grande colère :
— Je le sais, je le sais. Je l’avais dit pour rire. Gare à ne pas te vanter pour si peu ! Mais entre-temps mon Newton avait regretté sa phrase trop coupante.
— D’ailleurs, reprit-il un peu embarrassé, il y a ceux qui ne font pas très attention, et alors… même s’ils ne sont pas des ânes… je suppose…
Il me sembla qu’il m’offrait là une planche de salut, et dans un élan de sincérité :
— Ça doit être ça, dis-je. Je ne saurai jamais être attentif.
— Comment ?… Toi ? s’exclama le garçon en rougissant jusqu’à la racine des cheveux. Pourtant, j’aurais juré qu’au fond du fond, il avait une grande envie de rire.
Je lui mis une main sur la bouche :
— Chut, n’approfondissons pas l’enquête.
Ainsi, le théorème de Pythagore m’a coûté, comme on le voit, une nouvelle humiliation profonde. Malgré tout, je ne lui voue plus cette ancienne rancœur. Il ne régnera jamais la confiance entre lui et moi, mais je le considère comme un ami de la famille, auprès duquel il n’est permis de commettre aucune impolitesse, même s’il vous est personnellement antipathique.
-

Page de garde du recueil
Post-scriptum
L’introduction a été rédigée par C. S. Aravinda ; les traductions en français (de l’anglais pour l’introduction, de l’italien pour la nouvelle) sont de J. Germoni. Merci à Andrea Sambusetti pour quelques points épineux (comme une figue de Barbarie) de la traduction.
Article édité par Emmanuel Jacob





9h22
Voir les 5 commentaires