
Le CAPES (Certificat d’Aptitude au Professorat de l’Enseignement du Second degré) fut instauré dans les années cinquante. Son obtention, accessible par voie de concours, permet d’avoir un poste d’enseignant titulaire dans le Secondaire. En mathématiques, le concours consiste en deux épreuves écrites, d’une durée de cinq heures chacune, suivies d’épreuves orales pour les admissibles. Jusque il y a quelques années, elles avaient un sérieux contenu et étaient considérées comme très sélectives. Je me rappelle encore de bribes de conversations dans la salle des professeurs d’un lycée technique de la région Hauts-de-France où j’enseignais à temps plein en tant que Maître Auxiliaire (il y a de cela quelques décennies) :
— Il faut passer le CAPES, dit l’un.
— Oui, mais c’est dur, sélectif ! répond l’autre.
— Pourtant Untel l’a eu, rétorque un troisième.
— Mais tu n’as pas vu comme il a bossé sans relâche… comme un dingue !
Les non titulaires, tels les Maîtres Auxiliaires par exemple, savaient déjà à cette époque que c’est une bonne voie qui mène vers la titularisation et un meilleur salaire. Seulement, pour réussir, il faut travailler, travailler, et encore travailler, sans aucune certitude d’y arriver. Pour beaucoup, c’était un rêve… tellement difficile à réaliser !
Il y a presque une dizaine d’années, certains commencèrent à penser que c’était trop demander et que ça ne servait à rien d’avoir tant d’exigence pour ce que les lauréats allaient en faire dans les classes du secondaire… Peut-être, mais la formation était solide quand même, et c’est ce qui compte en premier.
L’organisation de ce concours a changé de forme en 2010. Sa durée de préparation a été rallongée d’un an et sa réussite définitive devint désormais conditionnée par l’obtention d’un Master, appelé à l’occasion Master enseignement. C’est la « masterisation » du CAPES dont la mise en marche effective sur le terrain – disons-le au passage – a demandé pléthore de réunions, infiniment longues. Officiellement, elle donnerait une « meilleure formation » aux candidats, en les obligeant à galérer un an de plus ! Mais il y avait d’autres raisons derrière… Effet immédiat de cette opération : la liste des candidats s’est mise à fondre peu à peu. Beaucoup des postes libérés, suite à des départs à la retraite, furent tout bonnement supprimés. Certaines classes dans des lycées et collèges sont restées sans enseignants pendant de longues périodes. Des établissements ont même cherché du côté de Pôle emploi, et quelquefois avec des annonces sur des sites comme le Bon Coin par exemple ! (Et pourquoi pas après tout ?) Et à ce jour, ce problème n’est pas encore résolu. (Cette vidéo qu’on peut aussi voir sur notre site dans ce billet est instructive.)
La formation a été désertée à tel point que le nombre de postes ouverts au concours a égalé à peu près celui des candidats. (La meilleure configuration pour réussir !) Le pourcentage des reçus a fortement grimpé, et a atteint les 100% dans la plupart des universités. Certaines d’entre elles ont même saisi l’occasion pour vanter leur préparation et afficher ces pourcentages vertigineux, alors même que le niveau de qualification des candidats retenus pose de vraies questions dont il n’est pas nécessaire d’en reparler, cela a été largement fait un peu partout et entre autres dans cette rubrique même (voir ici par exemple).
Une petite modification a été apportée quelques années plus tard mais qui n’a pas touché au contenu du programme, même si les épreuves sont devenues plus légères. C’est seulement à partir de cette année universitaire que ça a bougé. Le CAPES de Mathématiques comporte désormais deux options : une « Option Mathématiques » et une « Option Informatique ». Le choix de l’option se fait au moment de l’inscription. Ce qui a amené à modifier, substantiellement à la baisse, le programme sur lequel porteront au moins les examens écrits :
i) Une épreuve de mathématiques générales du « niveau classes préparatoires » pour ceux qui ont porté leur choix sur l’« Option Mathématiques » et d’informatique pour ceux qui l’ont porté sur l’« Option Informatique » (c’est l’Unité d’Enseignement UE1).
ii) Pour tous, une épreuve de mathématiques fondamentales portant sur les programmes de mathématiques du secondaire (c’est l’Unité d’Enseignement UE2).
Dans les instructions officielles il est explicitement dit pour l’UE2 que « Les notions traitées dans ces programmes doivent pouvoir être abordées avec un recul correspondant au niveau M1 du cycle master. » Cela signifie quoi ? Depuis 1982 j’interviens, sans discontinuer, dans les formations qui préparent aux concours de recrutement des enseignants du secondaire, et plus particulièrement la préparation au CAPES (initiée à l’Université de Valenciennes par celle du CAPES interne en 1989 où j’étais le premier intervenant). J’ai donc suivi de près l’évolution des choses jusqu’à ce jour. Mon point de vue sur cette dernière réformette ? Il prend en compte la situation malheureuse dans laquelle se trouve l’enseignement des mathématiques actuellement.
Je ne suis pas sans regretter l’ancienne formule qui, comme je l’avais dit, était sélective et d’un haut niveau. Une chose était au moins sûre : ceux qui décrochaient le CAPES avaient les bases requises et une vraie qualification pour enseigner les mathématiques dans les lycées et collèges. Je suis persuadé que lorsqu’on connaît bien les maths, on acquiert au bout de très peu d’années les bonnes méthodes pédagogiques. Je reprends encore la fameuse phrase : « Si vous saviez précisément ce que vous allez dire, vous le diriez bien. » de Gustave Flaubert, dissertant sur le contenu, l’idée, le style, la forme… Ou encore celle de Jacqueline de Romilly : « …on n’enseigne que ce que l’on sait. » dans L’enseignement en détresse . Les deux disent une évidence : pour enseigner bien, il faut bien connaître ce que l’on enseigne. (Mais ceci peut ne pas être toujours suffisant, je le reconnais !) Et c’est le moins qu’on puisse demander ! Que signifie alors « un enseignant doit bien connaître les maths ? » C’est avant tout :
- Bien connaître les objets mathématiques considérés, leurs définitions…
- Quand il s’agit d’un problème, comprendre son énoncé,
- ce qui le motive,
- savoir dégager une démarche pour le résoudre,
- bien découper cette démarche de façon graduelle,
- l’adapter à la situation.
- Pouvoir apporter des éléments de réponse aux questions curieuses et inattendues.
- …
Et ceci afin d’amener les élèves à bien voir de quoi il est question pour qu’ils puissent eux-mêmes, à leur tour, résoudre d’autres problèmes, du même type ou d’un type différent…
C’est une bonne chose que dans la nouvelle réformette on ait gardé une épreuve de cinq heures de niveau classes préparatoires (comme dans l’ancien système). Mais c’en est aussi une d’introduire cette UE2 du secondaire. C’est beaucoup plus sur celle-ci qu’il faut travailler avec les étudiants pour les amener à acquérir cette capacité de réflexion dont je viens de parler et être en mesure de transmettre le savoir mathématique quand ils seront à leur tour les instructeurs.
J’ai eu en charge cet enseignement dans mon université à cette rentrée. Je n’ai pas manqué d’expliquer à mes étudiants le but que je me fixe et je n’ai pas hésité non plus à leur rappeler, en toute franchise, les faiblesses qu’ils ont accumulées les années antérieures et la façon dont ils ont été « formés », basée essentiellement sur un apprentissage de recettes. Même si le niveau de cette UE2 ne vole pas haut, ils ne semblent pas y être à l’aise. Je leur ai alors proposé que, pour chaque séance, on choisisse ensemble un thème qu’on traiterait sous forme de dialogue, d’atelier, d’exercices… l’essentiel étant qu’ils s’impliquent et qu’ils prennent souvent des initiatives. Mais… même lorsque c’est élémentaire, j’ai relevé beaucoup de lacunes… et de bien bonnes ! Voici un exemple, pour ne pas rester dans le vague.
Le calcul d’aires est un des thèmes importants, menant de façon naturelle à la notion d’intégrale (traitée en Terminale). J’ai voulu l’aborder de façon élémentaire en proposant l’exercice suivant.
Exercice
Transformer géométriquement un quadrilatère en un triangle qui lui est équivalent, c’est-à-dire ayant la même aire.
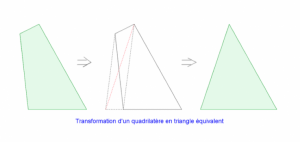
Je leur ai demandé comment ils allaient procéder. Personne n’a réagi, aucune idée n’a été avancée, pas la moindre prise d’initiative ! Il a fallu les faire démarrer, les pousser à chaque étape, à commencer par rappeler la formule donnant l’aire d’un triangle, comment on la justifie… et, à mon grand étonnement, beaucoup de ces étudiants (de Master 1, MEÉF !) ne savaient pas cela. La suite ne leur était pas évidente non plus. En somme, ça n’a pas été aussi cool comme je pensais que ça allait l’être sur des questions aussi faciles. Mais ils ont beaucoup apprécié à la fin parce qu’ils ont fini par apprendre et comprendre pas mal de choses. Ils avaient cette drôle d’impression d’être sortis d’une longue somnolence !
Personnellement, je trouve une bonne chose que cette unité d’enseignement soit mise en service dans la préparation au CAPES. Il suffit juste de savoir comment en faire bon usage.
Une tête pensante, c’est mieux qu’une tête remplie !





14h29
Voir les 9 commentaires