La vis … sans fin

• Maths et art

En songe Archimède ¹physicien, mathématicien grec (287-212 avant JC) inventeur de la vis qui porte son nom et qui aurait énoncé dans sa baignoire son fameux théorème : « tout corps plongé dans un liquide reçoit une poussée verticale égale au poids du volume déplacé » et qu’il en serait ressorti … (le corps …) mouillé ! Mais ce n’est pas ajouté … alors que nous en faisons tous la constatation. m’aurait invité à contempler la vis sans fin … m’informant, parallèlement, que ma vie ne sera pas sans fin et que ce n’était pas imputable à quelque vice de forme !

D’abord les résultats au petit exercice proposé dans le billet précédent.

Au rang \(n = 5\) : 140 boîtes ; au rang \(n = 6\) : 224 ; au rang \(n = 7\) : 336 ; pour passer du rang \(n\) au rang \(n+1\), on ajoute \(2(n+1)(n+2)\) boîtes ; au rang \(n\), il y a \(2/3 n (n+1) (n+2)\) boîtes, soit, comme il était demandé, … au rang \(n+1\), il y a \(2/3 (n+1) (n+2) (n+3)\) boîtes.

Maintenant

Dès lors qu’elle n’est plus plane, une surface a de quoi étonner. Il peut bien se faire que nous en ayons une connaissance théorique assez claire, que nous puissions énoncer toutes ses propriétés et demeurions émerveillés lorsque nous la regardons. Emerveillé peut sembler un terme un peu abusif en cette circonstance. Pour mon compte personnel, je ne le pense pas.

Le premier souvenir qui va dans ce sens remonte à l’école primaire. Dans la classe il y avait cet atlas représentant la terre … ce fut la première image que j’en eus. Puis me vint — dans un temps suffisamment éloigné, au regard de l’âge que je pouvais avoir alors — l’occasion d’être confronté au globe terrestre. La terre était ronde, cela je le savais, mais face à ce globe toute l’image que je croyais posséder, basculait. Je n’aurais pas su m’exprimer ainsi … mais il n’y avait pas de point de vue privilégié. Par exemple le pôle Nord, le Groenland qui sur l’atlas était blanc et assez étendu, pouvait apparaître petit et même disparaître.

Ceci semble bien naïf. Toutefois cela fait partie des impressions primaires qui se sont inscrites à jamais dans mon …(cerveau ?). La sphère est ronde et ceci pourrait expliquer cela. Mais il m’était arrivé de rouler une feuille de papier pour en faire un cornet. Je ne m’étonnais pas alors de réussir à rouler d’une certaine manière la feuille pour obtenir un cône plutôt qu’un cylindre … mais comme la feuille était rectangulaire … il y avait toujours une pointe (pas celle du sommet … mais je pense que vous avez compris car vous en avez certainement réalisé). Naïvement avec un ciseau je coupais cette pointe … et c’étaient d’autres pointes qui apparaissaient. Comment fallait-il donc couper pour faire disparaître ces pointes ? … puisque j’avais tout de même déjà croisé quelques cônes parfaits.

Je ne réfléchissais pas, dans le cas du cône, à l’étonnement qu’il y a d’obtenir une surface (non plane) en partant d’une surface plane. Bien avant d’avoir abordé en classe l’étude des surfaces développables ² pour en savoir plus sur les surfaces développables vous pouvez vous transporter de façon optimale ici et poursuivre là, par exemple j’avais été émerveillé par les copeaux que l’on obtient en perçant un morceau de métal ou bien avec l’outil au tour. Il y avait un certain plaisir à obtenir le copeau le plus long possible en cette forme « hélicoïdale » et il m’arrivait d’en conserver comme trophée. Certains pouvaient atteindre presque un mètre.

Si on réfléchit au copeau en terme de surface développable il y aurait matière à dire et redire ³ c’est plutôt une surface réglée qui n’est pas développable car lorsque qu’on essaie d’aplatir un morceau, il se casse. Ce qui ne devrait pas se produire si c’était une surface développable . Conjointement, sur ce tour qui fait les copeaux, il y a cette vis sans fin (une vis hélicoïdale carrée) pour entraîner le chariot porte-outil. Lorsqu’on observe et concentre son regard sur une vis sans fin en rotation, outre la fascination qui hypnotise de voir ces courbes en mouvement perpétuel ⁴dans le domaine sonore je songe au son descendant perpétuel que le compositeur Jean Claude Risset produisit par synthèse numérique dans les années 1970, voir ici aussi., il y a une certaine difficulté à saisir l’imbrication des courbes qui la composent. Lorsque, partant d’une rondelle de papier, on s’aventure à comprendre et réaliser cette surface il y a un étonnement à voir cette rondelle plane prendre « des allures tordues ». Pour mon cas personnel, la connaissance théorique que je puis posséder des surfaces développables, en cette expérience élémentaire, n’apporte rien de rassurant. Je pourrais même dire qu’elle ajoute de l’étonnement. Ce n’est peut-être plus de l’émerveillement, mais cela réserve de la surprise qui invite à réfléchir.

Faites l’expérience : tracez sur une feuille de papier rigide deux cercles concentriques. Tracez quelques lignes droites tangentes au cercle intérieur. Découpez la rondelle et tentez de former la surface hélicoïdale. La suite ne se décrit pas mais se ressent en manipulant. Si vous êtes attentifs vous observerez sans doute qu’une partie de chacune des tangentes que vous avez tracées reste droite ( enfin , espérons, car … la surface est aussi vivante qu’une anguille qui se débattrait entre vos doigts) et que l’autre se courbe. Tout ceci s’explique aisément. Le cercle intérieur est la ligne de rebroussement pour la surface que vous définissez et ces droites en sont les tangentes … la droite tangente demeure ligne droite mais au-delà du point de tangence elle … passe dessous. ⁵comme sur l’objet ici présenté, la surface se constitue de deux parties. Sur celui-ci j’ai fait la soudure sur le bord extérieur de mes deux rondelles. Il aurait fallut souder le long du cercle intérieur pour avoir la vraie surface hélicoïdale . Et alors, vous auriez constaté que la tangente demeure droite au-delà de la soudure .. passant d’une partie à l’autre ; de la face pile de la première partie, à la face … face de la seconde partie . Hors ce que vous voyez en est le dessus … Au-delà du point de tangence … votre ligne droite … change de nature … serais-je tenté de dire. En un sens, oui. En un autre, non, car elle continue à définir le chemin le plus court entre deux points !

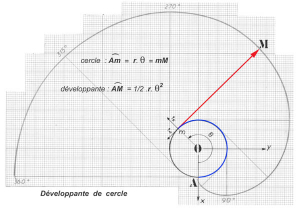
Les plus passionnés pourront tracer les lignes de courbure de cette surface … il y a en premier les droites … et puis leurs courbes orthogonales. Pour cela il vous suffit de tracer à plat sur votre rondelle les développantes du cercle intérieur … non pas spirales mais en forme d’escargot. ⁶pour saisir concrètement ce que représente cette développante de cercle vous pouvez imaginer avoir enroulé autour d’un cylindre une petite bande métallique élastique (en acier par exemple) et fixé à une extrémité un crayon. En conservant une des deux extrémités collée au cylindre, vous libérez lentement l’autre extrémité en déplaçant le doigt sur le cylindre, de façon que le reste demeure plaqué sur le cylindre. Comme la bande est élastique elle reprendra sa forme originelle (un segment de droite). Le crayon dessinera la développante de cercle. Vous pourrez observer que la courbe est perpendiculaire au segment. Le cercle est la développée de la développante !

Au menu ce soir : escargots et anguille ?

Allez, tout ceci est bien naïf, mais me rend les mathématiques aussi vivantes que cette anguille insaisissable qui se tortille … et me rend leur fréquentation riche… (de poésie ?)