
Il est question dans ce billet du bonheur que l’on peut ressentir devant la classification des polyèdres réguliers.
Dans un billet récent, Stéphane Jaffard parlait de la possible utilisation thérapeutique des mathématiques.
Ce thème pourrait aussi être exploré dans la littérature. Je désire l’illustrer ici par un extrait du Chapitre XIX du roman « La tante Tula » de Miguel de Unamuno 1Le titre original est « La tía Tula ». Il fut achevé en 1920. La traduction est mienne., montrant le bonheur ressenti par une femme qui a sacrifié sa vie aux autres, devant la classification des polyèdres réguliers :
Elle apprit avec Ramirin tout ce que lui avait à apprendre, car elle le suivait tous les jours dans ses devoirs. Elle satisfaisait ainsi son désir de savoir qui l’avait affligée depuis qu’elle était petite et qui fit que son oncle la compare un jour à Eve. Et parmi les choses qu’elle apprit avec son neveu pour les lui enseigner, peu nombreuses furent celles qui l’intéressèrent plus que la géométrie. Elle ne l’aurait jamais cru auparavant ! Mais dans ces démonstrations de géométrie, science aride et froide selon le sentiment des autres, Gertrudis rencontrait quelque chose d’indéfinissablement lumineux et pur. Bien des années plus tard, une fois adulte, et quand la poussière qui avait été la chair de sa tante reposait sous terre, sans lumière solaire, Ramirin se souvenait de l’enthousiasme avec lequel un jour de printemps radieux elle lui expliquait pourquoi il ne pouvait y avoir plus de cinq et seulement cinq polyèdres réguliers ; trois formés de triangles : le tétraèdre, de quatre ; l’octaèdre, de huit et l’icosaèdre, de vingt ; un seul de carrés : le cube, de six, et un seul de pentagones : le dodécaèdre, de douze. « Mais ne vois-tu pas comme c’est clair ? » me disait-elle — raconte le neveu — ; « tu ne le vois pas ? seulement cinq et pas un de plus, comme c’est beau ! Et ça ne peut pas être autrement, cela doit être ainsi ! », et en le disant elle me montrait les cinq modèles en bristol blanc, si blanc, qu’elle avait construits elle-même avec ses saintes mains, qui étaient prodigieuses pour tout labeur, et c’était comme si elle venait de découvrir elle-même la loi des cinq polyèdres réguliers … pauvre tante Tula ! Et je me souviens que, lorsque tomba sur l’un de ces modèles géométriques une tache de graisse, elle en fit un autre, car elle disait qu’avec la tache on ne voyait pas bien la démonstration. Pour elle la géométrie c’était de la lumière et de la pureté.
On peut ressentir de la joie non seulement à prouver ce théorème de classification ou à construire des modèles en carton des cinq polyèdres réguliers, mais aussi à savoir à peu près les représenter en perspective, comme s’ils étaient translucides. Voici par exemple des manières de dessiner les deux polyèdres ayant le plus grand nombre de faces, l’icosaèdre et le dodécaèdre.
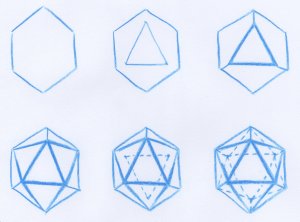
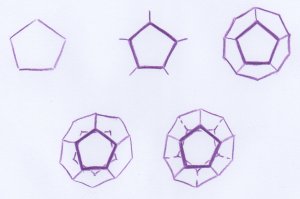
Facile, n’est-ce pas ? Hélas, les programmes actuels de géométrie au lycée rendent les polyèdres réguliers inaccessibles, car bien des pédagogues sûrement très bien intentionnés ont expliqué que les cerveaux des adolescents seraient trop brutalisés si on les obligeait ainsi à voir dans l’espace.
On calcule en revanche des points d’intersection de droites dans le plan. Je crains pourtant qu’une âme affligée par un labeur trop ingrat, comme celle de la tante Tula, n’y trouve point d’apaisement.

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.