La didactique des mathématiques

Un point de vue, une expérience, un témoignage !

Les enseignants du supérieur acceptent rarement de consacrer une partie de leur service statutaire à la formation pédagogique. Presque tous préfèrent les enseignements dits « classiques » pour des raisons diverses, dont une principale : ils pensent qu’ils sont moins prenants, ce qui leur permettrait de se consacrer plus « intensément » à leur travail de recherche. Et pourtant, la formation des enseignants à tous les niveaux devrait être une des priorités dans l’enseignement supérieur. Il est donc de « leur devoir » de s’y atteler autant que le reste.

Dans l’établissement où j’exerçais, le cours de didactique était dispensé par des enseignants de l’IUFM (Institut universitaire de formation des maîtres), devenu l’INSPÉ (Institut national supérieur du professorat et de l’éducation) après avoir eu au passage d’autres dénominations. Par manque d’effectif – lors d’une rentrée scolaire – je fus sollicité pour en assurer une partie. J’ai accepté même si j’avais déjà – et j’ai toujours eu – un volume horaire important dans la préparation aux concours du professorat des écoles, du CAPES et, pendant quelques années, de l’agrégation interne ; et ce, depuis que j’ai pris mes fonctions d’enseignant-chercheur (en 1981 à l’Université de Lille III).

J’ai donc débarqué par hasard en didactique. Et c’était une « bonne chose » ! J’ai eu une belle occasion de mettre en œuvre, auprès des étudiants que j’avais, se préparant au métier d’enseignant, une méthode qui me tenait à cœur : faire la leçon intégralement sous forme de dialogue pour les amener à se responsabiliser, à ne pas juste avaler les recettes qu’on leur sert. Au début, ils avaient un peu de mal à voir l’intérêt de la démarche. Mais ils ont fini par comprendre que pour avoir confiance en eux-mêmes et dominer ce qu’ils doivent communiquer, il faut qu’ils prennent conscience qu’ils ont déjà des connaissances, qu’ils peuvent sortir : il suffit à cet effet qu’ils fassent l’effort d’y réfléchir (réfléchir est une chose à laquelle, malheureusement, ils avaient beaucoup de mal à s’adonner !).

Qu’est-ce que la didactique ?

Si on veut une définition brève et concise, on s’en tiendra à celle que donne un dictionnaire (par exemple Le Petit Larousse) : science ayant pour objet les méthodes d’enseignement. Mais d’autres la définissent comme l’art d’enseigner. Pour moi, ce n’est ni complètement un art ni totalement une science, c’est un mélange des deux, et c’est tant mieux : les démarches didactiques paraissent générales, mais elles sont propres à chaque discipline. Quand il est à l’œuvre, le maître doit les adapter à la situation, en y mettant éventuellement sa touche personnelle. Une leçon de littérature ou d’histoire ne saurait être menée comme une leçon de mathématiques ou de physique… mais toutes doivent avoir un même but : transmettre à l’apprenti des connaissances tout en l’amenant à réfléchir dessus. C’est l’élément autour duquel s’articule le travail de la transmission du savoir. Une « bonne didactique » doit l’intégrer en son sein et en user, sinon elle ne restera que lettre morte.

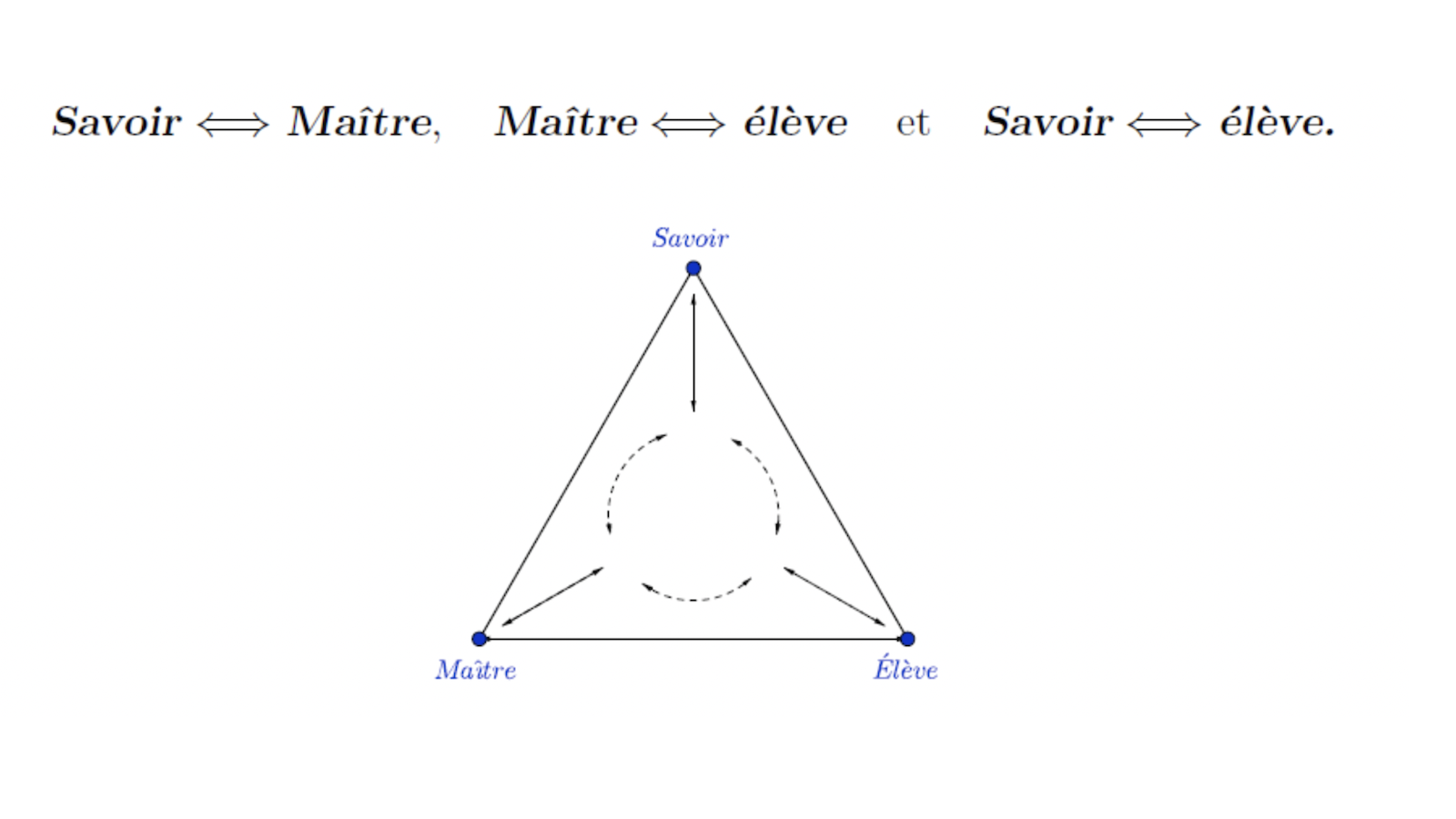
Les pôles de la didactique sont le savoir, le maître et l’élève. Ils sont les sommets du triangle didactique (comme on l’appelle dans le jargon de la discipline) dont les côtés schématisent les trois interactions bipolaires qu’on voit dans le logo ci-dessus. Elles décrivent respectivement les processus de formation, d’enseignement et d’apprentissage. Nous allons en donner une description rapide en nous limitant à ce qui nous intéresse ici : la didactique des mathématiques.

Le savoir

C’est l’ensemble des connaissances dans le domaine des mathématiques à travers ses spécialités : algèbre, analyse, géométrie, probabilités… pour ne citer que celles qui les composent de manière globale. Une partie de ce savoir est sélectionnée pour être transmise : ce sont les instructions officielles des instances ministérielles ; elles sont exécutées par des commissions dont les membres sont choisis en fonction de leurs compétences dans le domaine. Il s’agit de dégager ce qui est nécessaire d’enseigner à tel ou tel niveau. Les membres de ces commissions ont pour mission première de composer un programme d’enseignement et de le constituer en chapitres, de préférence classés de façon cohérente suivant les divers niveaux, et de sorte à faciliter le travail pédagogique des enseignants en charge.

Le maître

Son travail consiste à transmettre du « savoir » à l’élève. À cet effet, il doit posséder ce savoir et le dominer largement pour qu’il puisse le faire de façon efficace, certaine et aisée. C’est une condition nécessaire pour être un enseignant ; sans quoi, il n’est pas plus qu’une « caisse de résonance » : quelqu’un qui se contente simplement de répéter ce qu’il a entendu ou lu. La transmission du savoir à travers une leçon (un cours ou un travail dirigé) devient alors beaucoup plus facile quand le maître connaît parfaitement bien le contenu de ce qu’il doit communiquer. « On n’enseigne que ce que l’on sait » disait Jacqueline de Romilly. On peut aussi citer la fameuse maxime de Gustave Flaubert (grand maître de la littérature française du XIXe siècle) dissertant sur le contenu, l’idée, le style, la forme : « Si vous saviez précisément ce que vous voulez dire, vous le diriez bien ! » Tous les deux mettent en évidence une vérité incontestable : pour enseigner bien, il faut bien connaître ce que l’on enseigne ! Le maître doit donc avoir cette qualité. Mais que doit-il faire ensuite ? Fondamentalement, deux choses.

• Transformer le « savoir » en un « savoir transmissible » à l’élève : les données d’un programme d’enseignement sont souvent, et presque toujours, brutes et un peu vagues, probablement de façon délibérée pour laisser au maître une liberté d’interprétation et une prise d’initiatives propres.
• Un chauffeur de bus a constamment en tête le trajet qu’il doit faire de son point de départ à son point d’arrivée. À n’importe quel niveau, l’enseignant est dans la même situation : pour mener à bien sa leçon, il doit l’avoir bien préparée, en maîtriser et les éléments de base et les détails et, bien entendu, l’organiser de façon très accessible à son auditoire. Surtout, il ne doit pas se contenter de répéter ce qu’il a lu dans un manuel ou ce qu’il a appris par cœur la veille. Sinon, il ne pourra faire face à aucune situation imprévue, et encore moins répondre aux questions d’un élève éveillé.

Ne l’oublions pas, quelquefois les rôles peuvent s’inverser : l’élève peut apprendre des choses au maître (eh oui, ça arrive !). Ce dernier ne doit donc nullement s’en offusquer et admettre que, malgré tout, un enseignant ne peut pas tout savoir.

L’élève

C’est l’acteur principal, la « matière première » si on ose parler ainsi. C’est pour lui que le système est bâti car son rôle est de recevoir le savoir, auprès d’un maître. C’est son droit fondamental mais qui ne le dispense guère d’un « devoir » : celui de faire tous les efforts nécessaires pour que la transmission de ce savoir se fasse de manière effective. Et en ce sens, il ne doit pas se contenter de ce que le maître lui transmet. Il doit l’aider en faisant lui-même un travail parallèle : consultation d’ouvrages, usage d’outils divers (électroniques ou autres, ça ne manque pas à notre époque)…

Ainsi, les trois pôles du triangle didactique jouent des rôles a priori différents mais ils sont interconnectés par des contraintes imposées à la fois par les droits et les devoirs de chacun. L’enseignement se fait alors de manière efficace et rentable lorsque le tout fonctionne en parfaite harmonie, et si tout le monde y met sa bonne volonté. Si des dysfonctionnements ou des problèmes apparaissent, il appartient aux deux parties d’accepter la discussion et le dialogue pour les régler. Mais c’est beaucoup plus au maître que revient la prise d’initiative de ce travail, parfois si sensible, de concertation et de « réconciliation ».

Les mathématiques ne se comprennent bien qu’à travers les exemples. Souvent, une fois pressées, les théories générales se tassent au fond des placards – mais qu’on peut toujours chercher en cas de besoin. C’est ce qui me pousse à croire, et même me convainc fortement, qu’un cours de didactique doit être essentiellement basé sur des exemples, mais des exemples qui traversent plusieurs niveaux et portent sur divers thèmes. La discipline n’en manque pas, ils y sont assez diversifiés et permettent d’entrevoir toutes les démarches possibles.

Que le futur enseignant recevant un cours de didactique le sache : le but n’est pas de lui donner des recettes qu’il sortira devant ses élèves mais de lui montrer comment bien comprendre le thème qu’il compte traiter, découper ses parties principales, en dégager les liens, en donner une bonne motivation et le moyen le plus à même pour l’enseigner. L’enseignant didacticien doit commencer par une petite introduction à la démarche mathématique en général. Mais ce sera aux étudiants de prendre l’initiative, de dire comment ils perçoivent la leçon. C’est hautement plus bénéfique que de garder le fauteuil de celui qui ne fait que recevoir. Les capacités pédagogiques s’acquièrent essentiellement sur le terrain. Il faut donc qu’ils s’entraînent et prennent l’habitude d’y travailler un peu.