
Les films et les assertions paradoxales de Jean-Luc Godard, disparu récemment, ont mystifié plusieurs générations de cinéphiles. Ses déclarations sont-elles plus claires lorsqu’elles touchent aux mathématiques ? Il est intéressant de les comparer aux réflexions de Yuri I. Manin.
Le physicien Murray Gell-Mann a proposé d’imaginer le lecteur d’un journal, qui tombe sur un article dans un domaine qu’il connaît, si bien que les erreurs et les faiblesses de l’article lui sautent aux yeux… avant de poursuivre en toute confiance la lecture du reste du journal.
La leçon de Gell-Mann est bien sûr que la presse contient des erreurs et des approximations abusives qui ne sont pas détectables par le lecteur moyen. Autre conclusion : on peut porter un jugement sur la fiabilité globale d’une source d’information en examinant ce qu’elle affirme sur des sujets avec lesquels on est familier. 1Briefly stated, the Gell-Mann Amnesia effect works as follows. You open the newspaper to an article on some subject you know well. In Murray’s case, physics. In mine, show business. You read the article and see the journalist has absolutely no understanding of either the facts or the issues. Often, the article is so wrong it actually presents the story backward-reversing cause and effect. I call these the “wet streets cause rain” stories. Paper’s full of them. In any case, you read with exasperation or amusement the multiple errors in a story-and then turn the page to national or international affairs, and read with renewed interest as if the rest of the newspaper was somehow more accurate about far-off Palestine than it was about the story you just read. You turn the page, and forget what you know. Michael Crichton, Why Speculate (26 April 2002)

Le cinéaste Jean-Luc Godard, disparu le 13 septembre 2022, était un personnage controversé. Ses films ont toujours divisé la critique. Son usage de formules énigmatiques et radicales le faisait passer pour le grand patriarche du cinéma ou pour son vieil oncle bizarre. C’est selon.
Ainsi Werner Herzog a déclaré :
«Quelqu’un comme Jean-Luc Godard est pour moi de la fausse monnaie intellectuelle comparé à un bon film de de kung-fu»
Et Ingmar Bergman : «Je n’ai jamais rien retiré de ses films. Je les ressentais comme artificiels, faussement intellectuels et complètement dénué de vie.»2Ingmar Bergman, cité dans Secret Lives of Great Filmmakers: What Your Teachers Never Told You about the World’s Greatest Directors (2014) par Robert Schnakenberg]
ou encore
«J’ai le sentiment en permanence que Godard veut me dire des choses, mais je ne comprends pas ce dont il s’agit, et j’ai parfois le sentiment qu’il bluffe, et m’arnaque». 3Ingmar Bergman, dans une entrevue avec John Simon (1971)
Le critère de Gell-Man, appliqué au domaine mathématique, peut-il étayer de tels jugements ? Voyons cet enregistrement d’un entretien avec Jean Douchet.
Le passage qui nous intéresse débute à la minute 27, voir encore la minute 55 .
Godard met en opposition l’écriture d’un film avec le film lui-même, et puise dans les mathématiques une analogie inédite : la même opposition qu’entre l’algèbre et la géométrie.
Une telle mise en parallèle est peut-être surtout une illustration de la vision et de la psychologie de Godardƒ, et ne saurait être considérée comme une affirmation empirique. Pourtant, l’opposition entre algèbre et géométrie exposée ci-après par Yuri I. Manin semble faire écho à Godard.
«Les historiens des mathématiques du vingtième siècle ont argumenté pour et contre l’interprétation d’une partie considérable des mathématiques grecques comme de l’«algèbre géométrique». Un exemple est fourni par le dessin d’un grand carré divisé en quatre parties par deux droites parallèles aux cotés orthogonaux de telle sorte que deux parties soient encore des carrés. Ce dessin peut être lu comme une expression et une preuve de l’identité algébrique \((a+b)^2 =a^2 +b^2 +2ab\).»
Voilà le diagramme :
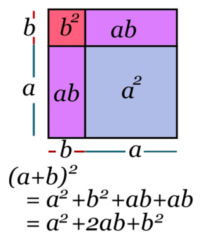
et Manin qui continue :

«Un tel passage à une perspective moderne suggère une considération plus générale de plusieurs modes de processus mentaux, en particulier ceux liés aux mathématiques. Voici les deux modes fondamentaux :
a) La manipulation consciente d’un système symbolique fini et discret, avec des lois explicites pour la formation de chaînes de symboles sensées, pour la construction de nouvelles telles chaînes, et des règles moins explicites pour décider quelles chaînes sont «intéressantes» (cerveau gauche, linguistique, activité algébrique).
b) La manipulation largement inconsciente d’images visuelles, avec un appel implicite aux statistiques issues des expériences passées, l’estimation des probabilités des événements à venir, et aussi l’évaluation de l’équilibre, de l’harmonie, de la symétrie (cerveau droit, arts visuels et musique, géométrie).
Les processus mentaux des mathématiciens au cours de leur recherche doivent combiner ces deux modes de multiples façons sophistiquées. Ce n’est pas là une tâche facile, tout spécialement en raison de la différence ahurissante des quantités de traitement de l’information, de l’ordre de 10 bit/sec pour le traitement symbolique conscient et \(10^7\) bit/sec pour le traitement visuel subconscient.» 4Yuri I. Manin, La connaissance mathématique : aspects internes, sociaux et culturels, dans Les Mathématiques comme Métaphore, Essais choisis, Traduit par : Claire Vajou, Préface de : Freeman J. Dyson, Postface de : Pierre Lochak. Voir l’original en anglais dont les passages ont été traduits ici par mes soins
Peut-être les avancées des neurosciences, avec l’identification des aires du langage et de la vision spatiale dans le cerveau, pourraient-elles clarifier cette distinction ? Mais revenons à Godard, qui va plus loin.
Il évoque, en citant Léon Brunschvicg 5Léon Brunschvicg, Descartes et Pascal lecteurs de Montaigne. Paris: Pocket, Éditeur, 1995 le remplacement des arguments géométriques des mathématiciens arabes et grecs par la géométrie analytique de Descartes. Il met en parallèle ce remplacement avec ce qu’il constate être la disparition de la «géométrie» dans le cinéma de notre temps.
Le passage ci-dessus de l’essai de Manin et sa suite ci-après fournissent encore une illustration du propos de Godard :
«Pour en revenir aux nombres réels et à l’«algèbre géométrique» des grecs, nous reconnaissons là un exemple de traitement par le cerveau droit d’un sujet qui, par la suite, évolua historiquement en quelque chose dominé par le cerveau gauche. »
Chacun appréciera la pertinence de l’analogie avec le cinéma.
Godard se risque ensuite à évoquer le théorème de Fermat, qu’il énonce de façon absurde ; mais il retrace correctement l’épisode de la marge trop petite pour contenir une démonstration. Il affirme sa conviction que Fermat possédait bien une démonstration très simple de nature géométrique, ce qui rejoint son idée personnelle que la géométrie s’est perdue.
Il est évident qu’il ne maîtrise pas le sujet, mais on peut être indulgent avec un homme âgé de 80 ans environ (j’ignore quand l’entrevue a eu lieu), qui n’a probablement plus guère pratiqué les mathématiques depuis qu’il en a été détourné après un passage en maths élém. Il faut encore un peu plus d’indulgence pour accepter son opinion sur la véritable démonstration de Fermat.
Il y a maintenant vingt-cinq ans, Jean Bricmont et Alan Sokal 6Jean Bricmont et Alan Sokal, Impostures intellectuelles, Odile Jacob 1997 ont dénoncé, chez les auteurs post-modernes, les abus de l’usage des concepts mathématiques et physiques. Godard ne me semble pas mériter de tels reproches. Il fait preuve d’une authentique curiosité, et a saisi, au moins en partie, les développements historiques. Il reconnaît ses limites en matière scientifique. Il me semble que son utilisation des mathématiques comme métaphore est un effort sincère et non dénué de mérite.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.