
C’est la période des déclarations d’impôts. Comme toujours à cette occasion, on entend des gens qui se plaignent : « C’est injuste ; cette année, j’ai gagné un peu plus, je saute d’une tranche et je vais devoir payer beaucoup plus d’impôts ». Il n’est peut-être pas inutile d’expliquer pourquoi ils se trompent.
Comment calcule-t-on l’impôt ?
Pour simplifier, considérons le cas d’un célibataire. Il faut d’abord connaître son revenu imposable pour l’année en question. Il s’agit du revenu du contribuable auquel on retire certaines sommes, par exemple au titre des frais professionnels (10 % forfaitaires pour beaucoup d’entre nous).
Ensuite, viennent les fameuses tranches qui donnent des taux :
- Jusqu’à 5 852 € : 0%
- de 5 852 à 11 673 € : 5,50%
- de 11 673 à 25 926 € : 14,00%
- de 25 926 à 69 505 € : 30,00%
- au-delà de 69 505 € : 40,00%
Mais cela ne signifie pas qu’on ne paye pas d’impôt si on gagne 5852 € et 5,50% de 5853 €, c’est-à-dire 322 €, si on gagne un euro de plus ! Si c’était le cas, effectivement, le système serait injuste. Un euro de plus de revenu et 322 € de plus sur l’impôt ! Cela signifie par contre la chose suivante :
Si le revenu est inférieur à 5 852 €, on ne paye pas d’impôt.
Si le revenu est compris entre 5 852 € et 11 673 €, on ne paye pas d’impôt sur les 5852 premiers € de son revenu, et on paye 5,50% de la partie qui excède 5852 €. Par exemple, si le revenu est 5 853 €, on payera 5,50% de 1 euro, c’est-à-dire 5 centimes (voir plus loin cependant ; on ne peut pas être imposé pour quelques centimes). Il n’y a donc pas d’injustice….
Si le revenu est compris entre 11 673 € et 25 926 €, on ne paye rien sur la première tranche de 5 852 €, puis 5,50% sur la deuxième tranche, allant de 5 852 € à 11 673 € (soit 5,50% de (11 673-5852) ou 320 €), et enfin 14,00% sur la partie du revenu qui excède 11 673 €. Exemple : si le revenu est de 15 000 €, l’impôt sera de 0 + 320 + 14 % x (15 000 – 11 673) = 785 €.
Et de même avec les autres tranches.
Voici un graphique. En horizontale, le revenu imposable. En verticale, l’impôt à payer.
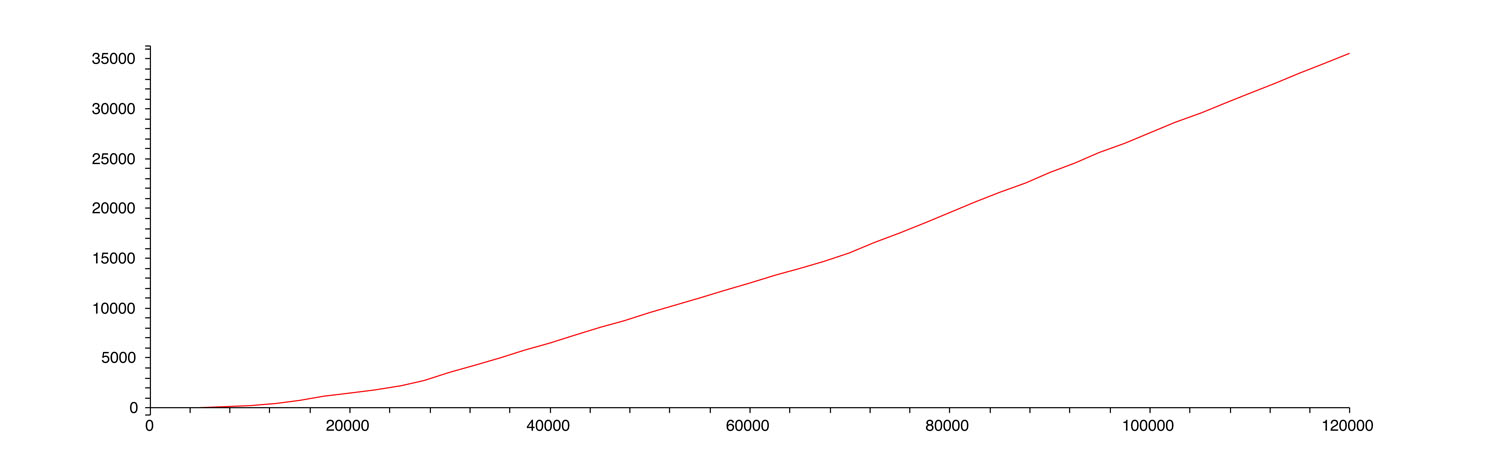
L’impôt comme fonction du revenu
Que remarque-t-on ? Que l’impôt est une fonction continue du revenu, comme disent les mathématiciens. Une petite modification du revenu n’entraîne qu’une petite modification de l’impôt. Sauter d’une tranche n’est pas un drame.
Voici le graphique responsable de la crainte du saut d’une tranche. En horizontale, encore le revenu imposable. En verticale, le taux de la tranche correspondante, qu’on appelle le taux marginal.
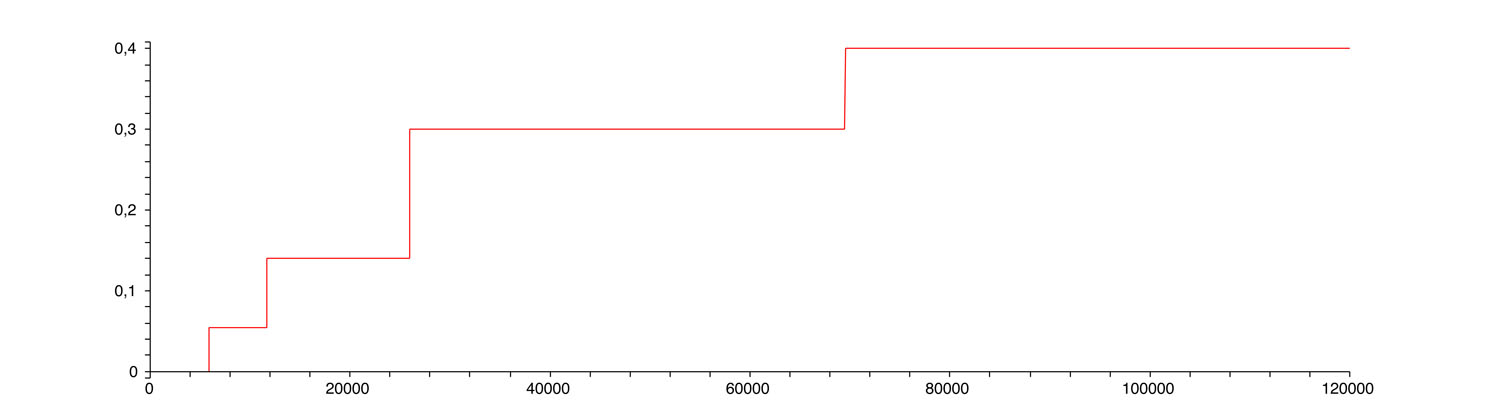
Le taux marginal en fonction du revenu
Ce graphique présente effectivement des sauts importants. Mais ces sauts ne concernent pas l’impôt… Ce graphique est intéressant cependant : il indique le pourcentage d’imposition qui serait appliqué sur chaque euro supplémentaire qui viendrait s’ajouter au revenu… Si votre revenu est de 30 000 € par exemple, sachez que pour chaque euro supplémentaire que vous gagnez, 30 centimes seront pour les impôts. Les mathématiciens disent que ce graphique représente la « dérivée de la fonction Impôt par rapport au revenu ». La fonction Impôt est donc continue mais pas sa dérivée.
Voici un troisième graphique. En horizontale, encore le revenu imposable. En verticale, le taux d’imposition global, c’est-à-dire le pourcentage qu’il faut appliquer au revenu pour avoir l’impôt. Si on appelle l’impôt I et le revenu R, il s’agit simplement de diviser I par R. Par exemple, si le revenu est de 50 000 €, l’impôt est de 9537 €, si bien que le taux global est de 9 537/50 000 = 0, 19, c’est-à-dire 19 %.
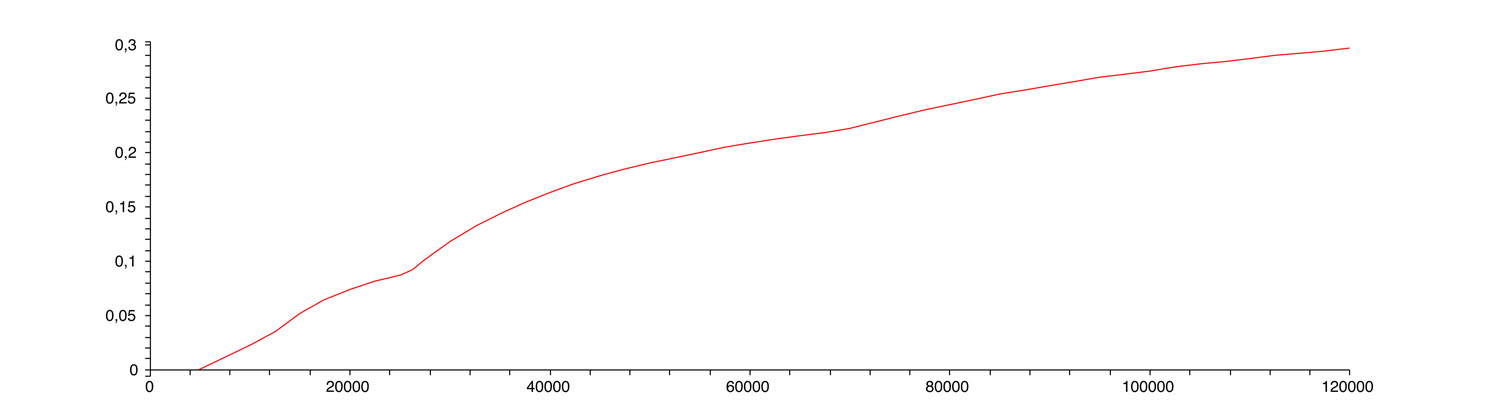
Le taux global comme fonction du revenu
Bizarre cette fonction. N’est-elle pas trop compliquée ? On peut bien comprendre que le système des tranches a une origine historique, datant d’une époque où les impôts étaient calculés à la main, mais aujourd’hui on pourrait imaginer quelque chose de plus « régulier » pour le taux global d’imposition. Par exemple, voici le graphique de la fonction 0.2(1+tanh((R−70000)/30000)) (tanh est la fonction qu’on appelle tangente hyperbolique que j’ai choisie sans véritable bonne raison, juste parce qu’elle « fait l’affaire ») :
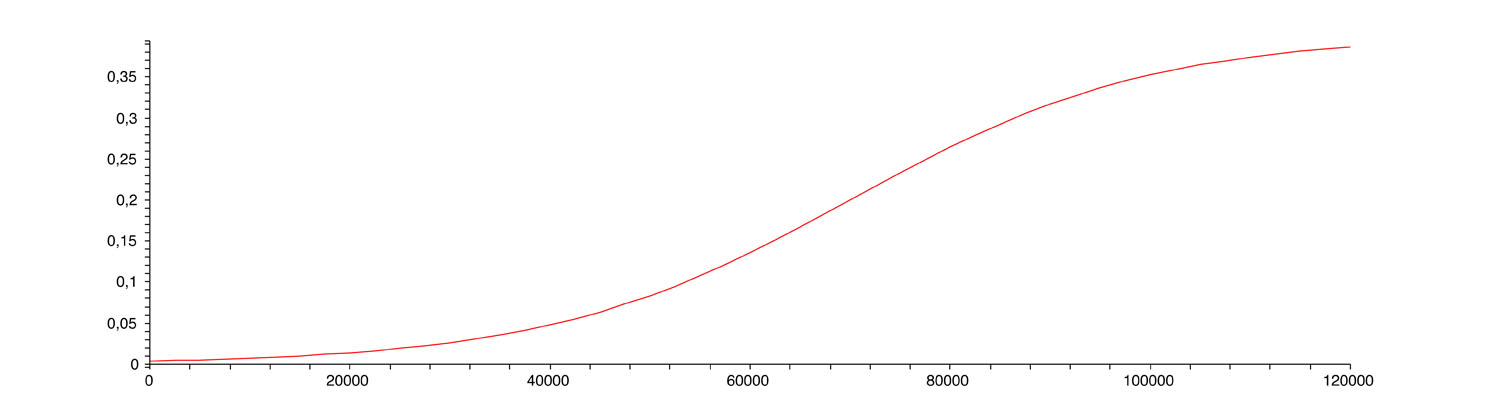
Une fonction mathématique
On pourrait suggérer au Ministère des Finances d’utiliser une fonction de ce genre ? Ce serait facile : pour calculer votre impôt, il suffirait de multiplier son revenu R par 0.2(1+tanh((R−70000)/30000)) ! Facile à faire avec n’importe quelle calculette… Plus facile encore que de calculer toutes ces tranches ! Bien sûr, le ministère pourrait ajuster les constantes dans cette fonction comme il le souhaite… Je me doute bien que ma proposition ne rencontrera pas d’écho !
Quelques remarques sur la fonction « Impôt »
Nous avons vu que cette fonction est continue. Elle est également croissante : plus le revenu est élevé et plus l’impôt est élevé : encore heureux !
Une autre propriété mérite d’être signalée car elle n’est pas évidente pour tout le monde. Voici encore un graphique. Horizontalement, toujours le revenu. Verticalement, on indique « ce qui vous reste quand vous avez payé vos impôts », autrement dit la différence entre le revenu et l’impôt.
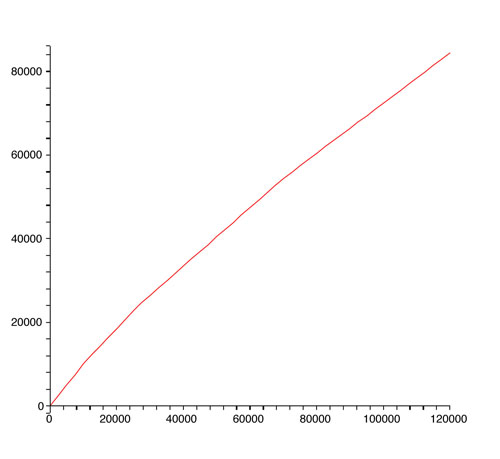
Ce qui reste après impôt
Eh bien, cette fonction est encore croissante. Qu’est-ce que cela signifie ? Tout simplement que plus on gagne et plus on est riche, même après avoir déduit les impôts… On entend trop souvent des affirmations selon lesquelles « ce n’est pas la peine que je travaille plus, car tout ce que je gagne en plus part aux impôts, et je suis perdant ».
Encore une propriété de la fonction impôt ? Un peu plus subtile… L’impôt est convexe. Cela signifie que la courbe « monte toujours plus vite » : plus le revenu est élevé et plus le taux marginal augmente. Non seulement l’impôt augmente en fonction du revenu (normal !) mais il augmente de plus en plus vite. Pour s’en convaincre, il suffit de regarder le premier graphique pour voir qu’il monte effectivement de plus en plus vite. Mais on peut aussi regarder le second graphique, celui du taux marginal, pour voir qu’il va en augmentant, et comme le taux marginal est l’accroissement de l’impôt, on peut donc dire que l’accroissement de l’impôt est croissant…
Quelques petits « détails »
Pour être précis, il faut ajouter quelques explications. D’abord, on ne paye pas d’impôt lorsque la somme à payer est inférieure à 61 €… D’autre part, les impôts inférieurs à 862 € bénéficient d’une décote qui est égale à la différence entre 431 € et la moitié de l’impôt théorique (compliqué tout ça…) Ces « détails » (inventés dans les années 80 par J. Chirac) ont quelques conséquences mineures sur ce que nous avons déjà dit et qui n’était pas tout à fait juste…
Voici quelques nouveaux graphiques qui prennent cela en compte. Le premier montre l’impôt. Horizontalement, on montre maintenant l’intervalle de revenu compris entre 10 000 € et 20 000 €.
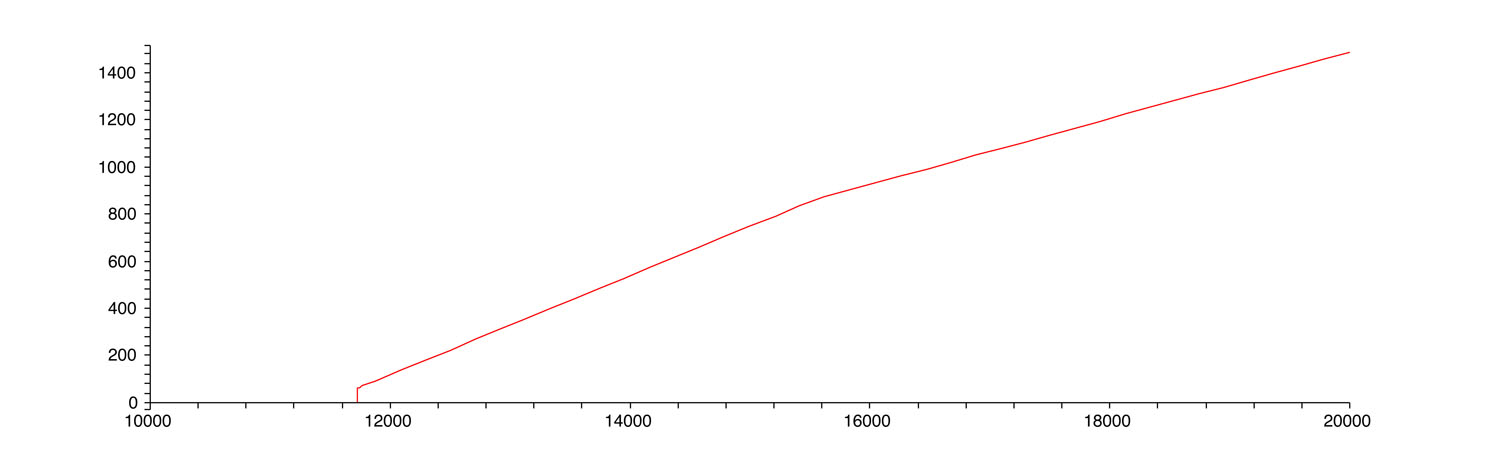
Impôt après décote
Le second montre le taux marginal, la dérivée du premier, sur tout l’intervalle de revenus de 0 €à 120 000 €.
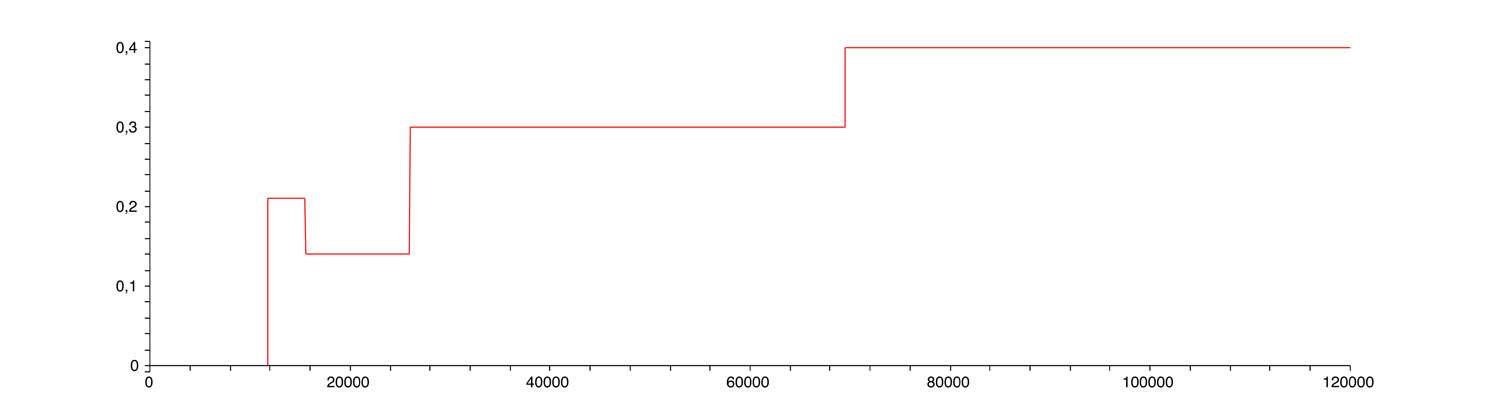
Taux marginal après décote
Que constate-t-on ? Il n’y a plus de taux marginal à 5 % ? Normal, puisque pour un célibataire imposé à 5 %, la décote annule l’impôt en fait. On constate ensuite un taux marginal qui est d’abord de 21 % avant de redescendre à 14 % ? Normal puisque lorsque le revenu est compris entre 11 729 € et 15 543 €, le taux marginal initial est de 14 % mais la décote va en décroissant lorsque le revenu augmente si bien qu’en pratique tout se passe comme si le taux marginal était augmenté et passe à 21 %.
Du coup, la fonction Impôt n’est plus convexe : elle augmente plus vite dans l’intervalle entre 11 729 € et 15 543 € que dans l’intervalle entre 15 543 € et 25 926 €. Perte de convexité ? Taux marginal qui n’est pas croissant ? Est-ce bien acceptable ?
Mais surtout, cette histoire de 61 € minimum montre que l’impôt n’est pas une fonction continue : elle présente une unique discontinuité lorsque le revenu est égal à 11 729 €. Pour ce revenu, vous devriez payer 61 €, mais vous ne les payez pas et on vous en fait « cadeau ». Si vous gagnez quelques € de plus, votre impôt passe à 65 €, et il n’y a plus de cadeau… Il y a donc bien un saut, pour ceux dont le revenu imposable est de 11 729 € !
Observons encore la courbe de « ce qui nous reste » mais en zoomant dans la région entre 11 500 € et 12 000 € :
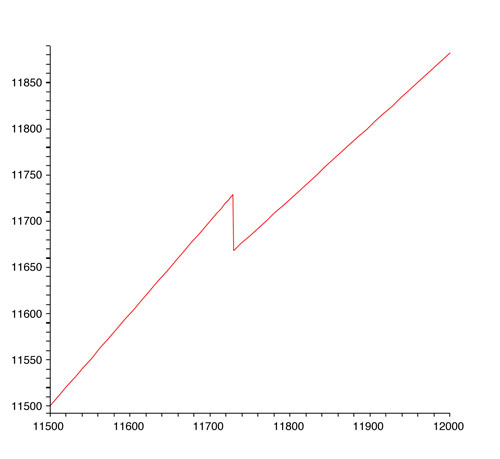
Zoom sur ce qui nous reste !
On aperçoit le même petit problème : « ce qui nous reste » n’est pas croissant précisément à cause de ce même point.
Un seul saut de 61 €. Pas si grave n’est-ce pas ?
Une rustine ?
C’était la situation jusque l’année dernière. Mais voici ce qu’on vient d’apprendre par le Ministère :
« À la suite du sommet social tenu le 18 février dernier, le Président de la République a voulu la mise en place rapide de plusieurs mesures de soutien du pouvoir d’achat, en faveur notamment de nos concitoyens les plus affectés par la crise économique. L’impôt sur le revenu est au cœur de ce dispositif. Ainsi, les contribuables imposés en 2009, pour leurs revenus de 2008, qui se trouvent dans la tranche d’imposition à 5,5 % vont bénéficier d’une réduction exceptionnelle des deux tiers de leur impôt sur le revenu. Les contribuables relevant du début de la tranche à 14 % bénéficieront également d’un allègement de leur impôt. »
Nous avons vu que la tranche à 5,5 % ne concerne pas les célibataires, puisqu’elle est annulée par la décote. En ce qui concerne la tranche à 14 %, voici ce qu’on lit sur le site du Ministère :
« Afin d’éviter un effet de seuil, les contribuables dont le revenu imposable par part est inférieur à 12 475 € bénéficieront d’un crédit d’impôt diminuant progressivement en fonction du revenu. Ce crédit d’impôt sera calculé de manière à valoir les deux tiers de l’impôt pour un revenu de 11 673 € (qui est la limite supérieure de la tranche à 5,5 %) et à devenir égal à zéro à la limite supérieure du dispositif, à 12 475 €.
Il nous faut donc ajouter une rustine à notre fonction impôt !
Pour un célibataire, le moins qu’on puisse dire est que cette réduction exceptionnelle est symbolique. Pour un revenu de 11 673 € , l’impôt après décote est de 49 € (et il n’est pas perçu) si bien que la « réduction exceptionnelle » est de 2/3 de 49 €, soit 32 €… La réduction décroît ensuite linéairement jusqu’à devenir nulle pour un revenu de 12 475 €.
Cela ne change que peu les courbes. Voici l’impôt final pour un revenu compris entre 11 800 € et 12 800 €. On voit le même saut (cette fois en 11 850 €) et une nouvelle brisure de la pente pour le revenu 12 475 €.
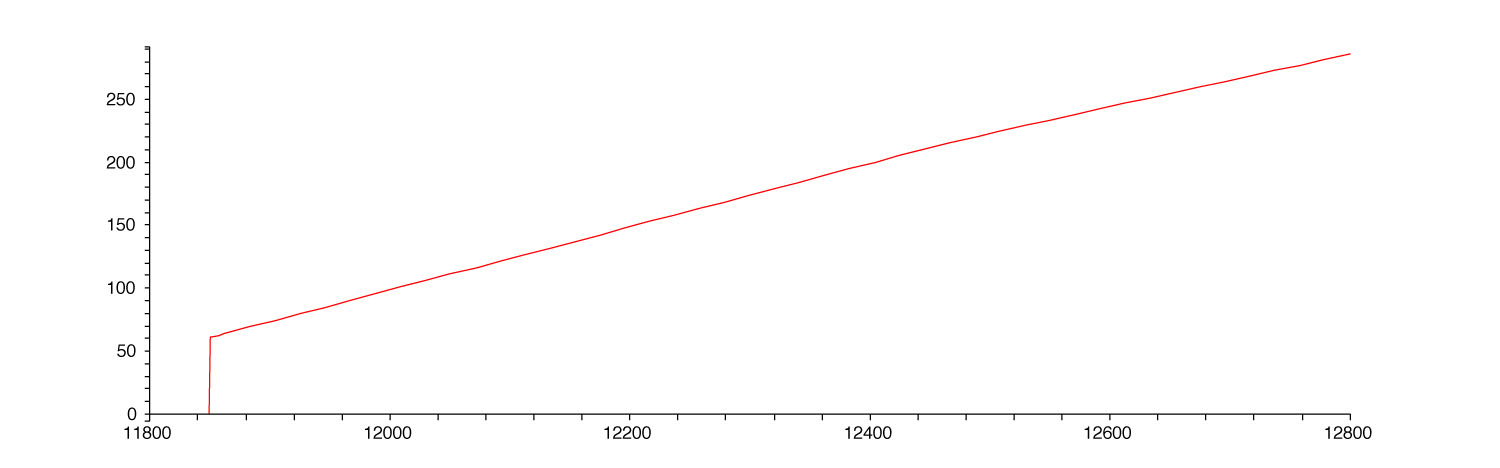
Impôt après décote et réduction
Et voici la courbe du taux marginal pour un revenu entre 10 000 € et 20 000 €. On voit bien un nouveau palier, entre 11 850 € et 12 475 € !
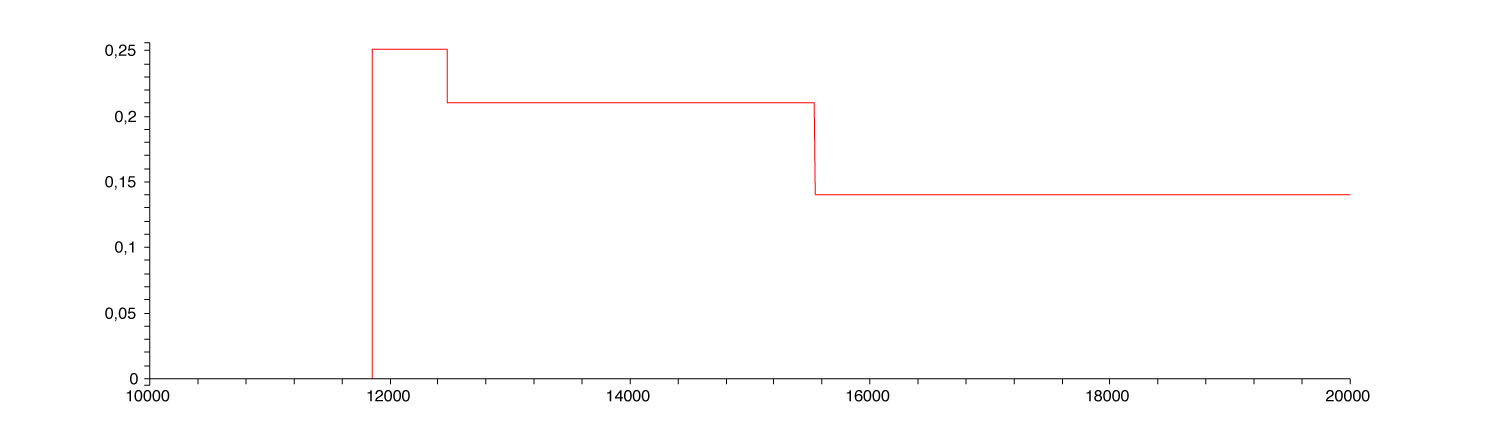
Taux marginal après décote et réduction
Pour être honnête, la réduction peut être plus intéressante dans le cas de familles.
Quel sera l’effet de la rustine qu’on ne manquera pas d’inventer l’année prochaine ? Finalement, une fonction tangente hyperbolique ne paraît pas si compliquée !
Et ce n’est pas tout !
L’impôt sur le revenu n’est bien sûr pas le seul impôt. Parmi les autres, il y a par exemple la taxe d’habitation dont on peut être exonéré si le revenu ne dépasse pas un certain seuil : quelle belle (ou monstrueuse) discontinuité de l’impôt ! Un euro de plus, on dépasse le seuil, et on doit payer la taxe ! Et il y a tant de prestations sociales qui sont « discontinues » : la prime pour l’emploi par exemple.
Et puis, il faudrait discuter de l’impôt d’un couple ou d’une famille. Pour un couple sans enfant par exemple, la méthode est la suivante. On prend la moyenne des revenus du couple, et on fait « comme si » chacun avait un revenu égal à cette moyenne et payait l’impôt correspondant (autrement dit, on divise le revenu du couple par 2, on calcule l’impôt comme ci-dessus, et on multiplie le résultat par 2). Si on y pense un peu, est-ce bien naturel de faire comme si un couple était constitué de deux célibataires gagnant chacun la moitié du total ? Après tout, il y a des dépenses partagées et on peut penser qu’un couple gagnant deux fois 2 000 € par exemple est « un peu plus riche » que deux célibataires gagnant chacun 2 000 €. Et puis, quelle est la « bonne » notion de moyenne qu’il faudrait utiliser ? Un billet récent montre que le concept de moyenne est un peu plus complexe que ce qu’on pourrait croire.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.