Intervalle de confiance : pourquoi tant de défiance ?

Le billet mis en ligne sur Images des Mathématiques par Pierre Arnoux et moi-même, le 1er octobre 2013, sous le titre Pourquoi enseigner les probabilités et la statistique dans les cours de mathématiques, puis le billet lui répondant mis en ligne par Pierre Colmez le 4 octobre, intitulé Mathématiques post-modernes, ont provoqué un certain nombre de commentaires de lecteurs. La critique faite par Pierre Colmez de la présence dans le nouveau programme des classes terminales des lycées français (filières S et ES) de la notion d’intervalle de confiance (dans le cas d’une proportion inconnue) ainsi que sa mise en cause de la présentation qui en est donnée dans ces programmes, ont amplement nourri ces échanges ; des enseignants de lycée, en particulier, ont écrit pour faire état de leur difficulté à enseigner, voire à comprendre, cette notion. Quoique je regrette un peu la concentration sur ce thème des réactions consécutives à notre billet, je n’en fus pas très étonné, ayant eu, depuis la parution des projets pour ces programmes, au printemps 2011, de nombreuses occasions d’enregistrer le trouble des professeurs sur ce thème.

Un paradoxe de cette situation est que l’intervalle de confiance (IC) est, de toutes les notions existantes de statistique inférentielle, celle qui est le plus couramment mise à contribution devant le grand public, avec les fameuses « fourchettes » des procédures de sondages ou de prévisions (électorales en particulier). A cet égard ce choix de l’IC comme aboutissement du programme de probabilités et statistique dans les lycées me paraît bien préférable au choix antérieur qui conduisait au test d’adéquation à une loi équirépartie, moins aisé à mettre en situation dans les classes et reposant en fait sur des mathématiques plus compliquées.

La défiance des enseignants vis-à-vis de l’intervalle de confiance repose à mon avis sur des obstacles à la fois épistémologiques, sémantiques et calculatoires. Ceux-ci me paraissent tous assez aisément surmontables, en s’appuyant sur des exemples élémentaires classiques du type sondage ou contrôle industriel de qualité. De plus en plus le matériel mis à la disposition des enseignants (documents ressources du ministère ¹Accessibles via : Eduscol, manuels …) apporte maintenant en général les clarifications nécessaires ; mais nombre d’enseignants ont besoin d’accompagnement pour entrer dans une logique qui ne leur est pas familière.

Nous allons passer en revue ces trois types d’obstacles, en y ajoutant une pincée de pratique, et même de déontologie statistique, dont je regrette qu’elle soit absente des programmes. Dans cette démarche, il nous arrivera de nous écarter de la lettre des programmes, en particulier pour mettre en évidence la dualité entre les notions d’intervalle de fluctuation (IF) et d’intervalle de confiance (IC), dualité qui, à notre avis, éclaire les seconds. Mais ces derniers ne figurent actuellement que dans des programmes de terminale et de ce fait leur présentation en classe est restreinte à l’usage de la version des intervalles de fluctuation qui est présentée à ce niveau (IF dit « asymptotique ») ; en revanche dans cet article nous évoquerons les IC également en liaison avec les versions d’IF introduites en seconde et première.

L’obstacle épistémologique tient au besoin de bien mettre en évidence le modèle général dans lequel l’intervalle de confiance prend son sens.

Au sortir de cours de calcul des probabilités dans lesquels on considérait UNE loi de probabilité modélisant une situation donnée, et pour laquelle on avait mis en place la notion d’intervalle de fluctuation (IF), l’élève doit bien comprendre que l’on a à considérer maintenant un modèle comportant toute une famille de lois de probabilités susceptibles de régir le phénomène considéré. A la modélisation d’une ignorance déjà traitée en calcul des probabilités, celle sur le résultat d’une expérience avant que celle-ci ait été effectuée (par exemple la couleur d’une boule qu’on va tirer dans une urne de boules de deux couleurs, de composition connue), s’en rajoute donc une seconde sur la loi à adopter pour ce phénomène (la composition de l’urne). Ce saut épistémologique dans la nature de l’ignorance à prendre en compte est bien sûr présent dans tous les textes rédigés à l’intention des enseignants. Il m’apparaît qu’il serait souvent bon de l’introduire avec plus de solennité ²Ceci est peut-être encore plus vrai pour l’initiation au test d’hypothèse figurant aussi dans le programme. On lit en général à ce sujet des phrases du type : « On fait l’hypothèse que la proportion inconnue vaut p0 ». J’ai vu des enseignants, à qui on avait expliqué qu’un modèle est la traduction mathématique d’hypothèses faites sur une fraction du réel, fournissant ainsi un cadre de travail pour l’analyse de ce réel, être fort troublés par le fait qu’on mette en cause une telle hypothèse. La langue anglaise est ici plus riche, qui dispose des mots « assumption » et « hypothesis », le premier plus fort que le second. Dans la situation de l’urne évoquée ici, « assumption » porte sur le fait que la probabilité de tirer une boule d’une couleur donnée est égale à la proportion, inconnue, de boules de cette couleur dans l’urne, et que, si on procède à des tirages avec remise, les résultats successifs sont indépendants. « Hypothesis » désignerait par exemple l’affirmation que les boules de chacune des deux couleurs sont en nombres égaux, affirmation que l’on soumettrait au feu de l’observation d’un échantillon tiré dans l’urne. Je pense que des précautions de langage peuvent être utiles ; pour ma part, quand je présente les justifications d’un modèle, j’aime bien dire « On admet que … » ; et quand j’énonce une hypothèse à tester, je préfère dire « On avance l’hypothèse que … », ou « On propose l’hypothèse que … », plutôt que « On fait l’hypothèse que … », qui laisse moins de place au doute.. Considérons ainsi les prévisions un soir d’élection ; pour être dans le cadre du programme de terminale nous nous limiterons à un vote tel un référendum, à deux expressions possibles, OUI ou NON (un second tour d’élection présidentielle en France est une situation analogue). Il existe une population, physiquement bien constituée, qui est celle de tous les bulletins comportant un suffrage exprimé et la proportion de ceux portant le vote OUI est, au moment de la clôture du scrutin,un nombre \(p\) à la signification physique indiscutable, mais à ce moment-là inconnu de nous. En première approximation (les techniques effectives de recueil sont un peu plus sophistiquées), le matériel sur lequel opèrent les prévisionnistes est un échantillon de \(n\) bulletins, considérés comme résultant de \(n\) tirages indépendants dans cette population. Si on note \(F\) la variable aléatoire « fréquence de bulletins OUI dans l’échantillon », \(nF\) suit donc une loi binomiale de paramètres \(n\) et \(p\). On a le même modèle en contrôle de qualité : une production de pièces bonnes ou mauvaises est supposée de qualité stable durant un certain temps, au cours duquel la probabilité pour chaque pièce produite d’être bonne est \(p\), inconnu ; le contrôleur extrait indépendamment, pour les observer, \(n\) pièces. Si la signification concrète de \(p\) varie selon ces deux exemples, il a à chaque fois le statut de « paramètre du modèle », selon la terminologie courante en statistique inférentielle, qui conduit à le mettre en indice au \(P\) qui signifie « probabilité » : d’où la notation \(P_p\).

Une caractéristique pratique de toutes ces situations expérimentales, qui est quasiment toujours omise dans les cours, est que n’est en fait jamais totale l’ignorance sur la valeur inconnue de \(p\). Autrement dit il n’est pas réaliste de modéliser en donnant comme ensemble de valeurs possibles de \(p\)  l’intervalle \(\lbrack 0 , 1 \rbrack\) tout entier. Les « experts » (politologues, industriels …) sont toujours capables de fournir des valeurs \(p_{-}\) et \(p_{+}\), vérifiant \(0 < p_{-} < p_{+} < 1 \), telles qu’il soit certain que \(p\) n’est pas en dehors de l’intervalle \(\lbrack p_{-} , p_{+} \rbrack\), qui apparaît donc comme l’ensemble des valeurs de \(p\) à retenir dans la modélisation ; on le notera \(D\) (pour « domaine de définition ») dans la suite. Cette remarque n’a pas pour seul but d’être réaliste ; nous verrons qu’elle permet aussi de gérer un obstacle calculatoire qui gêne souvent dans l’enseignement.

L’obstacle sémantique est double.

D’une part on s’exprime parfois (en particulier dans des sujets d’examen) avec un article défini (Calculez l’intervalle de confiance au niveau de confiance 0,95) alors que, la définition faisant intervenir une inégalité, il n’y a pas unicité de l’objet ; évidemment il y a à chaque niveau d’étude un non-dit, à savoir qu’il est demandé de fournir la variété d’IC alors introduite en classe (avec en général un niveau de confiance fixé à 0,95) ; mais ce non-dit se raffine quand on avance en niveau scolaire.

D’autre part, et encore plus générateur de trouble, est le fait que la propriété caractérisant un IC, relativement au paramètre \(p\), au niveau de confiance \(1- \alpha\) est souvent exprimée par une phrase du genre : la probabilité que \(p\) appartienne à cet intervalle est supérieure ou égale à \(1- \alpha\). La syntaxe de cette phrase induit dans la tentation de penser que \(p\) est aléatoire, ce qui n’est pas le cas dans le modèle considéré³C’est autour de ce risque de malentendu que se sont largement déroulés les échanges sur Images des Mathématiques évoqués au début de ce billet..

Il est bien préférable, quoique de sens identique, de dire (ce qui est bien le cas dans le libellé du programme) :

La probabilité que cet intervalle aléatoire contienne \(p\) est supérieure ou égale \(1- \alpha\),

ou même, si on veut insister sur le modèle dans lequel on se place :

Quel que soit \(p\) appartenant à \(D\), la probabilité, si \(p\) est la valeur du paramètre, que cet intervalle aléatoire contienne \(p\) est supérieure ou égale à \(1- \alpha\),

phrase qui, formellement, peut s’écrire, si on note respectivement \(C_{-}\) et \(C_{+}\) les variables aléatoires extrémités de l’IC (ici fonctions de la fréquence observée \(f\)) :
\[\forall p \in D\;\;P_p\lbrack C_{-} \leq p \leq C_{+} \rbrack \geq 1 – \alpha.\]

Les obstacles calculatoires apparaissent dans la mise en œuvre de la dualité entre intervalle de fluctuation (IF) et intervalle de confiance (IC)⁴Des critiques ont été exprimées contre l’introduction de l’expression « intervalle de fluctuation », qui n’est usitée que dans le cadre scolaire, au contraire de « intervalle de confiance » qui relève du vocabulaire usuel de la statistique. Pour ma part je considère qu’avoir bien nommé cette notion a un avantage pédagogique certain. Quoique la notion d’IF soit en soi de nature probabiliste (et non statistique), elle ne prend vraiment son sens qu’en tant qu’outil de statistique inférentielle ; elle sert alors aussi bien pour la notion de test statistique (à laquelle les élèves sont initiés sous la terminologie « prise de décision », mais que nous laissons en dehors du champ de cet article) que pour celles d’intervalle de confiance ou de demi-droite de confiance, cette dernière également non traitée ici.
.

On note tout d’abord la présence de définitions formellement différentes de l’IF selon les programmes : il y en a d’explicites, en commentaires ou en notes, dans les programmes de seconde et de terminale (S, ES et spécialité en L). Ceci constitue une source de trouble pour certains enseignants mais ce trouble peut être levé s’ils comprennent qu’il n’y a pas unicité de cet objet mais que, pour une loi de probabilité donnée, sur \(\Bbb R\) ou un intervalle de \(\Bbb R\), est intervalle de fluctuation au seuil \(1 – \alpha\) tout intervalle dont la probabilité est supérieure ou égale à \(1 – \alpha\)⁵Cette absence d’unicité est bien mise en évidence dans le document de ressources en Probabilités et Statistique pour la classe de terminale en page 19 (début de la section IV intitulée « Intervalle de fluctuation ») ; on y trouve des considérations sur les contraintes pour le choix de l’IF analogues à celles que nous présentons ici. .

Formellement, avec cette définition, \(\lbrack 0 , 1 \rbrack\) est un IF pour n’importe quelle valeur de \(\alpha\) mais il est clair que, pour fournir une information pertinente sur \(P\), un intervalle de fluctuation n’a d’intérêt que s’il n’est « pas trop gros »; cependant les IF compatibles avec un \(\alpha\) donné sont d’autant plus proches de \(\lbrack 0 , 1 \rbrack\) que \(\alpha\) est plus petit. On cherchera donc à trouver (et enseigner), sous certaines contraintes techniques (ou pédagogiques), variables selon les circonstances, des intervalles de fluctuation aussi courts que possible, éventuellement calculés de manière approchée.

Voici quelques exemples de contraintes possibles usuelles, déclinées ici dans le cadre du programme : loi de la fréquence observée dans un échantillon de taille \(n\) tiré dans une population où on considère un caractère à deux modalités dont l’une est de proportion \(p\) ; les IF sont alors des sous-intervalles de \(\lbrack 0 , 1 \rbrack\) dépendant de \(p\) et seront donc notés \(I(p)\).

1. Se limiter à quelques (voire une) valeur de \(\alpha\)(en particulier \(\alpha = 0,05\)).
2. Chercher à rendre le calcul aussi simple que possible (par exemple en faisant en sorte que l’intervalle ne dépende de \(p\) que par la position de son centre mais pas par sa longueur).
3. Mettre des conditions sur \(n\) et sur \(p\) en dehors desquelles l’intervalle proposé \(I(p)\) est susceptible de ne pas satisfaire la condition imposée \(P_p(I(p)) \geq 1 – \alpha\) ; la condition sur \(p\) peut intégrer celle évoquée plus haut selon laquelle, pour des raisons de modélisation, \(p\) doit être pris dans un sous-intervalle \(D\) de \( \rbrack 0 , 1 \lbrack \).
4. Utiliser un intervalle symétrique autour de \(p\) (espérance mathématique de la loi de la fréquence).
5. Imposer que, si on note \(I(p) = \lbrack A_{-}(p) , A_{+}(p) \rbrack\), alors \(P_p (\lbrack 0 , A_{-} (p) \lbrack) \leq \frac{\alpha}{2}\) et \(P_p (\rbrack A_{+}(p) , 1 \rbrack) \leq \frac{\alpha}{2}\).
6. Imposer (ce qui semble « de bon sens ») que les fonctions \( A_{-}\) et \( A_{+}\) définies au point 5 ci-dessus soient croissantes.

Par commodité d’usage, la condition 3 peut parfois n’être satisfaite qu’approximativement, \(P_p(I(p))\) pouvant, pour certains couples \((n,p)\) satisfaisant cette condition, être « un peu » inférieur à \(1 – \alpha\), cette « défaillance » étant jugée par les praticiens non gênante pour leurs applications.

Les conditions 4 à 6 portent sur les IF dits bilatéraux, auxquels se limite le programme. On pratique aussi des intervalles unilatéraux, qui seraient ici de la forme \(\lbrack 0 , A(p) \rbrack\) ou \(\lbrack A (p) , 1 \rbrack\)⁶En note 4, on évoquait d’autres applications statistiques des IF que celles aux IC (implicitement bilatéraux) étudiés ici. Ainsi, étant fixée une valeur \(p_0\) du paramètre, les IF bilatéraux servent pour tester des hypothèses du type \(p=p_0\) et les IF unilatéraux servent pour tester des hypothèses du type \(p \geq p_0\) ou du type \(p \leq p_0\), très utiles en fiabilité industrielle. Les IF unilatéraux servent aussi pour fabriquer des demi-droites de confiance.
.

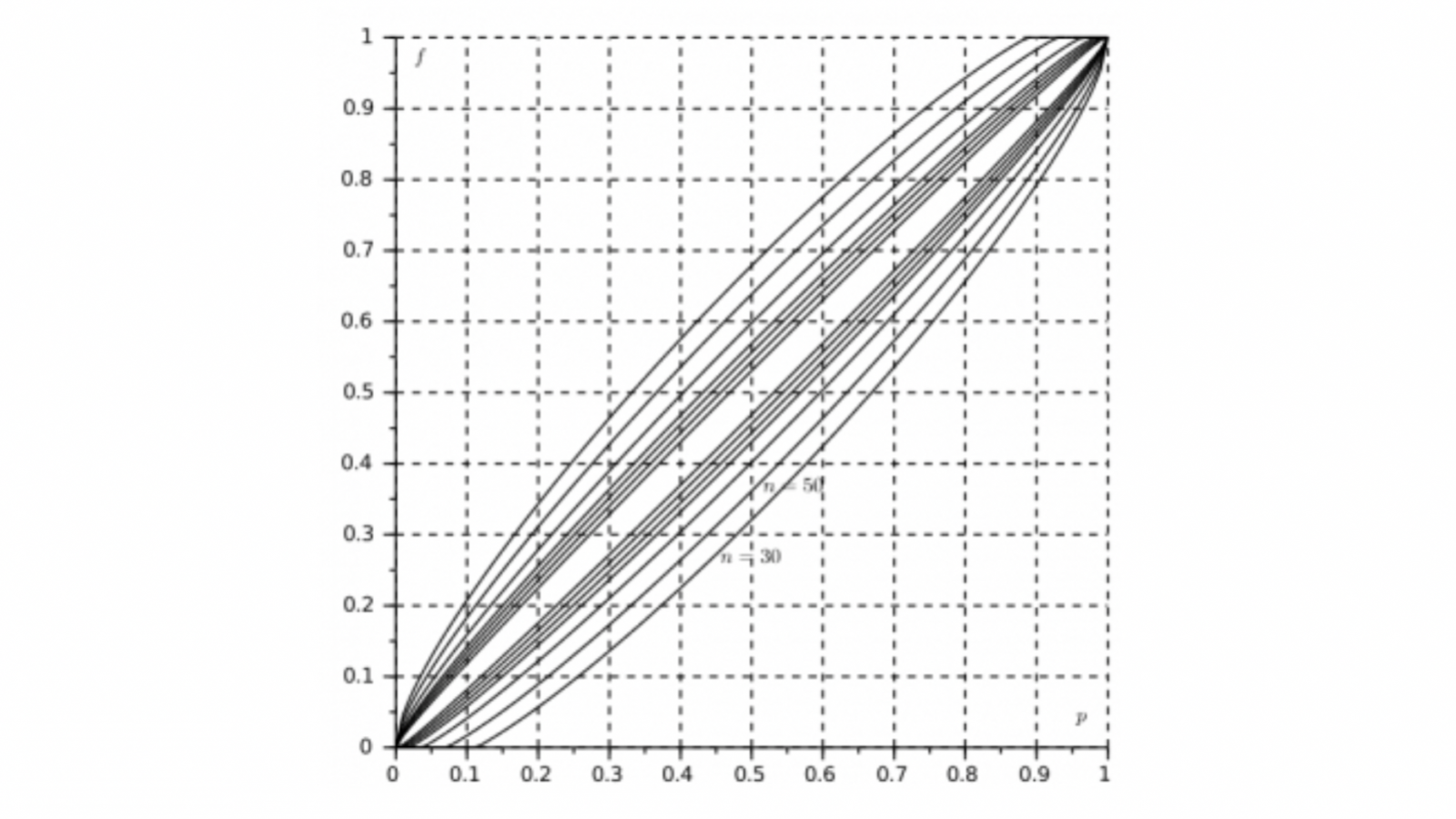
La condition 6, satisfaite dans tous les cas de choix d’IF pratiqués, permet de visualiser graphiquement la dualité entre IF et IC. Dans le carré \( \lbrack 0 , 1 \rbrack ^2 \) (ou plus précisément le rectangle \(D \times \lbrack 0 , 1 \rbrack \)) les fonctions \( A_{-}\) et \( A_{+}\) dessinent un « fuseau » comme il apparaît dans la figure ci-dessous où, pour \(1 – \alpha = 0,95\), sont superposés les graphes des extrémités des IF pour les valeurs suivantes de \(n\) : 30, 50, 100, 200, 300, 500, 1000.

Soit \(K\) l’ensemble des couples \((p,f)\) tels que \( A_{-}(p) \leq f \leq A_{+}(p)\) : un IF \(I(p)\) se lit en coupant ce fuseau par la verticale d’abscisse \(p\). Et il résulte de la définition même des intervalles de confiance que l’on obtient une famille d’IC, \(J(f)\), en coupant ce fuseau par des horizontales, par la suite d’équivalences :
\[ f \in I(p) \Leftrightarrow (p,f) \in K \Leftrightarrow p \in J(f). \]

En d’autres termes, si \( A_{-}\) et \( A_{+}\) sont continues et strictement croissantes, sauf éventuellement sur les intervalles où elles prennent les valeurs 0 (ce qui peut être le cas pour \( A_{-}\) pour \(p\) proche de 0) ou 1 (ce qui peut être le cas pour \( A_{+}\) pour \(p\) proche de 1), les fonctions extrémités inférieure et supérieure des IC, notées ci-dessus \(C_{-}\) et \(C_{+}\), sont définies sur \(\rbrack 0 , 1 \lbrack\) comme les fonctions réciproques⁷Notion dont il est fort regrettable qu’elle ne figure plus explicitement au programme des classes terminales, même scientifiques. respectivement des fonctions \( A_{+}\) et \( A_{-}\).

Cette condition analytique technique de stricte croissance et continuité n’est pas satisfaite dans le cas des IF tels qu’ils sont définis en classe de première (voir détails ci-dessous) car alors leurs extrémités appartiennent à l’ensemble dans lequel les fréquences prennent effectivement leurs valeurs, c’est à dire l’ensemble des multiples de \(\frac{1}{n}\) entre 0 et 1 ; alors les fonctions croissantes \( A_{+}\) et \( A_{-}\) ne sont ni strictement croissantes ni continues mais ont des paliers. Comme il n’est raisonnable de n’effectuer ces études que pour \(n\) assez grand (la condition classique \(n \geq 25\) est à cet égard minimale), il est naturel de « lisser » les fonctions \( A_{-}\) et \( A_{+}\) en fonctions strictement croissantes et continues. C’est cette solution (dont nous verrons qu’elle peut avoir des justifications asymptotiques) qui était utilisée pour les représentations graphiques dites abaques, telles la figure ci-dessus, qui ont longtemps été l’outil de base des statisticiens (ou utilisateurs de statistique) devant calculer des IC.

Nous passons maintenant en revue les choix d’IF proposés dans les programmes actuels des lycées en France avec, que ceux-ci soient au programme ou non, les IC qui leur sont associés, ainsi que des précautions de calcul qu’ils imposent.

En seconde sont proposés les IF \( \lbrack \sup (0 , p – \frac{1}{\sqrt{n}}), \inf (1, p + \frac{1}{\sqrt{n}}) \rbrack \)⁸On lit en général, dans les programmes ou manuels, \(\lbrack p – \frac{1}{\sqrt{n}} , p + \frac{1}{\sqrt{n}} \rbrack\), intervalle qui sort de \(\lbrack 0, 1 \rbrack\) si \(p < \frac{1}{\sqrt{n}}\) ou si \( p> 1 – \frac{1}{\sqrt{n}}\), circonstances qui peuvent être, pour \(n\) assez grand, évitées si \(p \in D\)., qui satisfont toutes les contraintes 1 (pour \(\alpha = 0,05\)) à 6 citées ci-dessus (oh combien pour la contrainte 2 !), la contrainte 3 prenant la forme \(n \geq 25\), \(np \geq 5\) et \(n(1-p) \geq 5\)⁹Contraintes faiblement « défaillantes » pour certains couples \((n,p)\), au sens de la mise en garde qui suit immédiatement la liste des six conditions ci-dessus ; observer s’il en est ainsi, et avec quelle ampleur, est un exercice assez élémentaire sur tableur ; une telle possibilité peut s’obtenir en adaptant le fichier Excel présenté dans le document ressources de terminale (voir note 11 ci-dessous) ou en utilisant un exercice (n°52) fourni dans le manuel Math’x de Terminale ; on trouve ainsi, par exemple, que pour \(n=201\) et \(p = 0,45\), la probabilité de l’intervalle \(\lbrack p – \frac{1}{\sqrt{n}} , p + \frac{1}{\sqrt{n}} \rbrack\) est 0,948, donc légèrement inférieure à 0,95., ces deux dernières inégalités étant affaiblies dans le programme en \(0,2 \leq p \leq 0,8\). Il n’est pas possible d’en donner une justification aux élèves à ce stade, puisqu’il s’agit d’un élargissement des IF présentés en terminale (voir ci-dessous), fondé sur les inégalités \(p(1-p) \leq \frac{1}{4}\) et \((1,96)^2 < 4\) ; cet élargissement est donc d’autant plus dommageable, en termes de précision de l’intervalle, que \(p\) est plus loin de \( \frac{1}{2}\).

Remarquons, quoique ce ne soit pas au programme de seconde (mais les documents d’accompagnement de terminale y reviennent), que des IC s’en déduisent élémentairement par l’équivalence \[ p – \frac{1}{\sqrt{n}} \leq f \leq p + \frac{1}{\sqrt{n}} \Leftrightarrow f – \frac{1}{\sqrt{n}} \leq p \leq f + \frac{1}{\sqrt{n}}. \] Mais une difficulté surgit car les IF utilisés pour déterminer les IC ne sont proposés que sous une condition faisant intervenir \(p\), à savoir \(\frac{5}{n} \leq p \leq 1 – \frac{5}{n} \) ; or maintenant \(p\) est inconnu. C’est là que l’on voit qu’il est utile que l’intervalle de définition de \(p\), soit \(D\), introduit dans la modélisation de la situation étudiée, soit contenu dans l’intervalle \(\lbrack \frac {5}{n} , 1 -\frac {5}{n} \rbrack\), ce qui est d’autant mieux réalisé que \(n\) est plus grand.

En première on propose des IF fondés sur la « vraie » loi de la fréquence et donc sur la loi binomiale. La contrainte privilégiée est ici la contrainte 5, portant séparément sur les majorations, par \(\frac{\alpha}{2} = 0,025\), des probabilités des deux intervalles dont l’union est le complémentaire de l’IC. La contrainte 4 (symétrie autour de \(p\)) n’est pas satisfaite et la contrainte 2 (simplicité) repose sur la fourniture d’un algorithme de calcul des extrémités de l’IF. La contrainte 3 (conditions sur \(n\) et \(p\)) n’a pas lieu d’être puisqu’on dispose ici d’un calcul exact (encore que les programmes de calcul des loi binomiales sur ordinateur incorporent des approximations, mais « indolores » car très précises). Dans la pratique, comme on l’a dit plus haut, l’obtention des IC associés s’effectue à partir des lissages continus des extrémités des IF évoqués ci-dessus à propos des abaques ; mais dans ce cadre l’IC n’est pas au programme des lycées !

Enfin, en terminale, on introduit les IF fondés sur la convergence des lois binomiales vers la loi normale quand la taille de l’échantillon, \(n\), tend vers l’infini et donc sur les approximations que cela autorise ;  or cette convergence est d’autant plus rapide que \(p\) est plus proche de \(\frac{1}{2}\) ; en fait les démonstrations classiques, à l’aide de la formule de Stirling, du théorème de la limite centrale font intervenir \(np(1-p)\) ; plus cette valeur est élevée, plus rapide est la convergence. Il n’est donc pas étonnant que la qualité de l’approximation soit présentée avec des conditions type « assez grand » portant à la fois sur \(n\), \(np\) et \(n(1-p)\), les bornes fournies traduisant les exigences sur cette qualité ; traditionnellement ce sont respectivement 25, 5 et 5, mais dans certains contextes on pourrait être plus exigeant. C’est le calcul sur la loi normale qui fournit alors, pour \(\alpha = 0,05\)¹⁰Auquel est associé \(1,96\) comme fractile (autrement dit quantile) d’ordre \(1 – \frac{\alpha}{2} = 0,975\) de la loi normale centrée réduite., l’IF dit « asymptotique », \( \lbrack A_{-}(p) , A_{+}(p) \rbrack \), avec \( A_{-}(p) = \sup (0, p – 1,96 \frac{ \sqrt{p(1-p)}}{\sqrt{n}})\) et \( A_{-}(p) = \inf (1, p + 1,96 \frac{ \sqrt{p(1-p)}}{\sqrt{n}}) \) (fonctions qui ont présidé à la confection de la figure ci-dessus)¹¹Le calcul exact de la probabilité de cet intervalle, à l’aide de la loi binomiale de paramètres \(n\) et \(p\) est possible avec le fichier Excel fourni dans le document ressource de Terminale, dénommé exploration_intervalle_de_fluctuation_asymptotique.xls . Il satisfait aux conditions 2 (il reste de calcul assez simple), 3 (en reprenant la forme la plus courante, qui nécessite à nouveau les mises en garde figurant dans la note 11), 4, 6 et, surtout, 5 : c’est celle qui préside à sa fabrication, en arrivant, grâce à la stricte croissance et la continuité de la fonction de répartition de la loi normale, à rendre exactes à \(\frac{\alpha}{2} = 0,025\), dans le cadre de l’approximation gaussienne utilisée, les probabilités des deux intervalles dont l’union est le complémentaire de l’IF.

On réalise donc alors au mieux le souhait de rendre l’IF aussi court que possible compte tenu des contraintes imposées. Et les IF vus en seconde apparaissent bien, comme on l’a déjà indiqué, comme des grossissements de ceux-ci, ce qui permet de comprendre pourquoi on donnait déjà alors les conditions de validité, sur \(n\), \(np\) et \(n(1-p)\), utilisées pour des formules plus précises. Dans la ligne de ce qui a été dit en note numéro 10 pour les IF donnés en classe de seconde, on remarque que la détérioration de l’approximation gaussienne quand \(p\) est proche de 0 et de 1 se traduit ici aussi par la nécessité de faire figurer (ce qui est sous-entendu dans les formules écrites dans les programmes ou manuels), les \(\sup(0,.)\) et \(\inf(.,1)\) dans les définitions de \(A_{-}(p)\) et \(A_{+}(p)\). Si on pose \(p_0 = \frac{1}{1 + \frac{n}{{1,96}^2}}\), c’est sur l’intervalle \(\lbrack 0, p_0 \rbrack \) que \(A_{-}\) prend la valeur 0 et c’est sur l’intervalle \(\lbrack p_0, 1 \rbrack \) qu’elle est continue et croît strictement de 0 à 1 ; de même c’est sur l’intervalle \(\lbrack 1 – p_0 , 1 \rbrack \) que \(A_{+}\) prend la valeur 1 et c’est sur l’intervalle \( \lbrack 0, 1-p_0 \rbrack \) qu’elle est continue et croît strictement de 0 à 1. Pour fabriquer la famille des IC, \(\lbrack C_{-}(f) , C_{+}(f) \rbrack \), associée à cette famille d’IF, il suffirait alors théoriquement d’introduire les fonctions \(C_{-}\) et \(C_{+}\), sur \(\lbrack 0 , 1 \rbrack \) comme respectivement les fonctions réciproques de \(A_{+}\) et \(A_{-}\), (avec les conventions \(C_{-}(1) = 1 -p_0\) et \(C_{+}(0) = p_0\)) ; ils seraient « aussi courts que possible » compte tenu du niveau de confiance 0,95¹²La généralisation à tout niveau de confiance \(1 – \alpha\) est évidente, en remplaçant dans les formules \(1,96\) par le fractile d’ordre \(1 – \frac{\alpha}{2}\) de la loi normale centrée réduite. . Mais cette approche purement mathématique néglige le fait que les IF utilisés sont asymptotiques, c’est-à-dire fondés sur des approximations qui ne sont valides que (en reprenant la forme la plus courante) pour \(n \geq 25\) et \(\frac{5}{n} \leq p \leq 1 – \frac{5}{n}\). Or \(p\) est par essence inconnu ; c’est alors qu’il est utile de se rappeler que le modèle utilisé supposait que \(p\) appartienne à un intervalle de définition \( D = \lbrack d_{-}, d_{+} \rbrack \) déterminé par des considérations empiriques (« dialogue » avec l’utilisateur de l’étude statistique, par exemple, pour revenir aux cas présentés ci-dessus, le politologue ou le contrôleur industriel), avec \( d_{-} > 0\) et \( d_{+} < 1\) ; il est donc « honnête » de ne fournir d’intervalle de confiance que si \(n\) est assez grand pour que \(D \subset \lbrack \frac{5}{n} , 1 – \frac{5}{n} \rbrack\), et cet intervalle est alors \(\lbrack C_{-} , C_{+} \rbrack \cap D\).

Cette manière de « refuser », en considérant le modèle, de calculer un IC si les conditions de validité ne sont pas satisfaites, est à notre avis bien plus conforme à la déontologie du statisticien que celle qui consiste à poser comme condition de validité, comme il est en général « pédagogiquement » recommandé, \(n \geq 25\), \(nf \geq 5\) et \(n(1-f) \geq 5\). Ceci revient en effet à effectuer un « transfert » sur \(f\) des conditions, portant sur \(p\), pesant sur le calcul des IF ; un autre défaut de cette pratique, proposée dans certains manuels, est qu’elle fait sans le dire usage de l’estimation ponctuelle de \(p\) par \(f\), dont le principe même est en dehors du programme et dont la théorie et la pratique sont au moins aussi délicates que celle des IC¹³Un autre cas où le statisticien se doit d’affirmer qu’il n’est pas en mesure de fournir un IC est celui où \(\lbrack C_{-}(f), C_{+}(f) \rbrack \cap D = \emptyset \), ce qui ne peut se produire que si \(p\) est « très proche » de 0, avec des probabilités en fait faibles si \(p \in D \).
.

Reste une dernière étape technique pour obtenir les IC donnés dans le programme : inverser les fonctions \(A_{+}\) et \(A_{-}\), restreintes respectivement aux intervalles \(\lbrack 0 , 1- p_0\rbrack \) et \(\lbrack p_0, 1 \rbrack \) ; il s’agit de résoudre des équations du second degré, admettant chacune, dans \(\lbrack 0, 1 \rbrack\), une unique racine. Les nombres \( f – 1,96 \frac{ \sqrt{f(1-f)}}{\sqrt{n}}\) et \( f +1,96 \frac{ \sqrt{f(1-f)}}{\sqrt{n}}\) sont des approximations de ces racines, d‘ordre 1 en \(\frac{\sqrt{f(1-f)}}{\sqrt{n}}\). Et, à ce stade, on peut revenir une fois de plus sur le contexte épuré vu en seconde et comprendre pourquoi des IC de la forme \( p – \frac{1}{\sqrt{n}} \leq f \leq p + \frac{1}{\sqrt{n}}\) sont des grossissements de ceux, \( f – 1,96 \frac{ \sqrt{f(1-f)}}{\sqrt{n}}, f +1,96 \frac{ \sqrt{f(1-f)}}{\sqrt{n}}\), qu’on vient de fabriquer; ils sont donc valides sous les mêmes conditions, mais moins précis.

Ces dernières considérations de technique de calcul, si elles sont à la portée des enseignants, dépassent certes le niveau des élèves de terminale. Faudrait-il pour autant renoncer à leur enseigner les intervalles de confiance ?

Je ne le pense pas, car, outre l’intérêt pratique des IC, il me semble important que, à ce niveau, les élèves prennent conscience que l’emploi des mathématiques repose largement sur des approximations et que ces approximations peuvent avoir deux types de justifications : usage, « à distance finie », d’un résultat asymptotique et simplification dans un calcul. Que la justification de ces calculs approchés ne puisse pas être entièrement fournie à leur niveau n’est pas grave ; la démarche scientifique suppose une certaine part de confiance à l’égard des résultats obtenus par ceux qui nous ont précédés. L’important est de savoir qu’il existe des règles de vérification de la validité de ces approximations aux degrés de précision couramment exigés et d’être capable de vérifier si celles-ci sont satisfaites. A ce titre l’enseignement des intervalles de fluctuation et des intervalles de confiance fournit une occasion intéressante de mise en place de considérations plus générales d’application des mathématiques, et en particulier, au fil de la progression des outils de la seconde à la terminale, de la tension qui existe toujours entre la volonté de précision (ici la faible longueur des intervalles de confiance) et le coût en termes de calculs de cette précision.