Hydrodynamique

• Systèmes dynamiques
• Physique

• Ressources pédagogiques

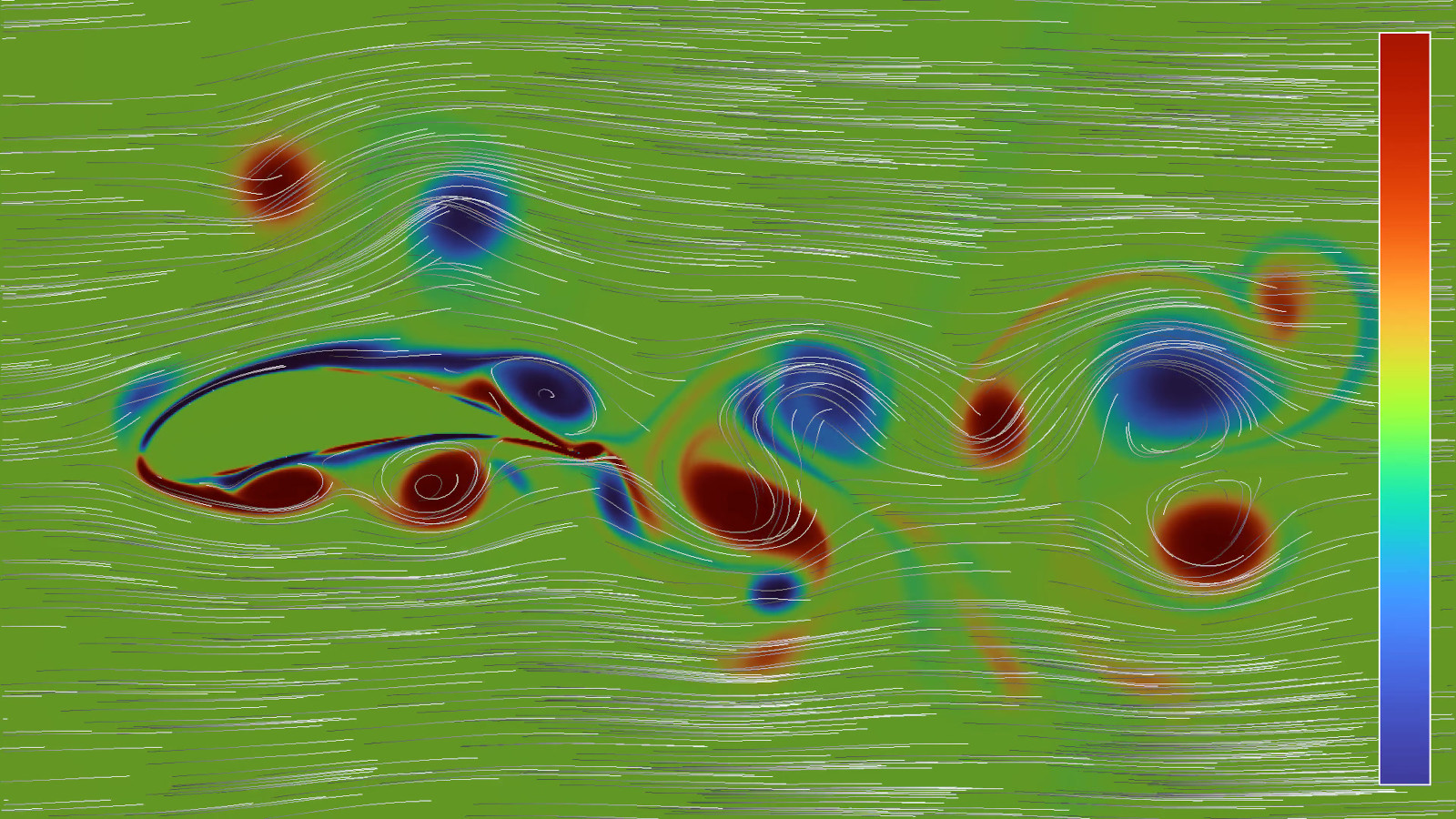
Vortex de Von Kármán

Les vortex de Von Kármán sont des tourbillons qui se forment lorsqu’un fluide et un obstacle se rencontrent avec une vitesse relative suffisamment grande. La vidéo montre une simulation des équations d’Euler compressibles avec conditions aux bords périodiques. Un obstacle en forme d’aile d’avion est représenté par une force répulsive fortement localisée. La vitesse relative du fluide est imposée aux bords gauche et droit du rectangle, et augmente au cours du temps. Cela permet de voir des vortex se développer lorsque la vitesse est assez grande. La vidéo, en quatre parties, montre d’abord la vorticité du fluide, qui mesure sa quantité de rotation, puis sa densité, qui est directement liée à sa pression. Les deux dernières parties montrent la même évolution en accéléré, avec un facteur d’accélération de 3. Le champ de vitesse du fluide est matérialisé par des traceurs passifs, qui se comportent comme des particules dont la vitesse est égale à celle du fluide.

Représentation 3D d'un écoulement de cisaillement sur le tore

Cette simulation des équations d’Euler incompressibles montre un écoulement de cisaillement dans le plan, la troisième dimension représentant la vorticité du fluide, qui mesure sa quantité de rotation. L’état initial est formé de plusieurs bandes parallèles, dans lesquelles la vitesse est différente. Cette configuration est répétée périodiquement dans le plan, et perturbée légèrement dans la direction perpendiculaire, afin de la rendre instable. Cette vidéo en deux parties montre la même évolution avec deux palettes de couleur et deux variables verticales différentes. Les deux parties montrent la vorticité du fluide, mais sur une échelle linéaire dans la première partie et sur une échelle logarithmique dans la seconde partie.

Écoulement de cisaillement sur le tore

Cette simulation des équations d’Euler incompressibles montre un écoulement de cisaillement. Les bords gauche et droite de la région rectangulaire sont identifiés, ainsi que les bords supérieur et inférieur, ce qui correspond topologiquement à un tore. L’état initial est formé de plusieurs bandes horizontales, dans lesquelles la vitesse est différente. Cette configuration est perturbée légèrement dans la direction verticale, afin de la rendre instable. Le phénomène observé d’inversion de la position des bandes, passant d’horizontales à verticales, est peut-être causé par les dimensions du rectangle. En partant avec des bandes verticales, ou dans un domaine carré, il n’est pas sûr que cette inversion se produirait.

Cette vidéo en deux parties montre la même évolution avec deux palettes de couleur différentes. Les deux parties montrent la vorticité du fluide, qui mesure sa quantité de rotation, mais sur une échelle linéaire dans la première partie, alors que dans la seconde partie l’échelle est logarithmique.

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
'''
-------------------------------------------------------------------------------
!                                                                             !
!                             Polygones réguliers                             !
!                                                                             !
!       Dessins géométriques et artistiques avec votre micro-ordinateur       !
!                                                                             !
! Jean-Paul DELAHAYE                                             pages 9 à 11 !
-------------------------------------------------------------------------------
'''


from outils_communs import nom_fonction, trace, finition
from math import pi, cos, sin
import matplotlib.pyplot as plt


def polygone_régulier(qo, lw, k, cx, cy, r, ad):
    np = 1000
    plt.figure(figsize=(12, 12))
    lix, liy = list(), list()
    for i in range(k+1):
        lix.append(np*(cx+r*cos(2*i*pi/k+ad)))
        liy.append(np*(cy+r*sin(2*i*pi/k+ad)))
    finition(lix, liy, qo, lw)


###############################################################################
def dessin_1(qo, lw):
###############################################################################
    nom = nom_fonction().capitalize().replace('_', ' ')
    polygone_régulier(qo, lw, 4, .5, .5, .45, pi/4)
    return nom


###############################################################################
def dessin_2(qo, lw):
###############################################################################
    nom = nom_fonction().capitalize().replace('_', ' ')
    polygone_régulier(qo, lw, 3, .5, .5, .45, 0)
    return nom


###############################################################################
def dessin_3(qo, lw):
###############################################################################
    nom = nom_fonction().capitalize().replace('_', ' ')
    polygone_régulier(qo, lw, 3, .5, .5, .45, pi/2)
    return nom


###############################################################################
def dessin_4(qo, lw):
###############################################################################
    nom = nom_fonction().capitalize().replace('_', ' ')
    polygone_régulier(qo, lw, 5, .5, .5, .45, pi/2)
    return nom


###############################################################################
def dessin_5(qo, lw):
###############################################################################
    nom = nom_fonction().capitalize().replace('_', ' ')
    polygone_régulier(qo, lw, 8, .5, .5, .5, pi/8)
    return nom


###############################################################################
def dessin_6(qo, lw):
###############################################################################
    nom = nom_fonction().capitalize().replace('_', ' ')
    polygone_régulier(qo, lw, 20, .5, .5, .4, 0)
    return nom

###############################################################################

if __name__ == '__main__':
    tit = 0             # 0 pas de titre sur l'image, 1 titre sur l'image.
    enr = 'svg'         # 0 pas d'enregistrement, 2 png + sgv
    axes = 0            # 0 pas de tracé des axes, 1 tracé des axes.
    qo = 1              # 0 noir et blanc, 1 couleur.
    lw = .7             # finesse du trait.
    réso = 300          # 300 dpi

    choix = range(1, 7)
    #choix = [1]
    total = len(choix)
    ouv = 0 if total > 10 else 1

    for fg in choix:
        total -= 1
        print(total, end=' ')
        dessin = eval("dessin_"+str(fg))
        nom = dessin(qo, lw)
        if qo : nom +="_c"
        if not(tit) : nom +="_st"
        trace(nom, tit, enr, axes, réso, ouv)

Test Guillemets

J’écris côté visuel : plus simple pour mettre des liens. J’écris une phrase « en mettant des guillemets ». Puis je veux que cette phrase soir en italique. Alors je la sélectionne et je clique sur le I. Et ça donne ça « en mettant des guillemets« . Sauf que dans le visuel, côté édition,  le guillemet est correct alors je ne me rends pas compte qu’il n’est pas dans le bon sens.

On ne  s’en rend compte qu’en prévisualisant à la relecture et on a du mal à tout corriger parce qu’on ne voit pas où on doit corriger. Le truc c’est qu’il faut d’abord mettre les guillemets puis tout sélectionner avant de mettre en italique : « en mettant des guillemets »

Mais quand on rédige, il y a parfois des guillemets dans des guillemets et c’est la pagaille.

Bref, est-ce que Mattieu pourrait faire en sorte que l’on voir le rendu dans la partie édition en visuel ?

Tests sur les images : des problèmes subsistent

On ne peut pas centrer une image ou choisir la taille vignette si on ne met pas de légende.
Par conséquent quand on a une image sans légende, on est obligé de mettre un point dans la légende.
Pas très propre comme solution.

Idem que pour les guillemets : le côté visuel diffère de la prévisualisation.

Ici la même image avec des tailles différentes sont publiées avec à peu près la même taille sur le site
(mais des résolutions différentes).

 

f second ne fonctionne pas

\(f »\) \(f »\) \(\f »\)

\(f’\)

Je ne me rappelle plus la solution que tu avais trouvée Maï :
On avait mis \prime deux fois.

Mais cette solution est assez lourde en écriture, que faire pour l’alléger?

avec  » : on a f »

avec deux fois \prime : \(f{^{\prime}}{^{\prime}}\)

Test Titre avec maths \(q^2\) touristes en \(q+1\) jours par groupes de \(q\), pour \(q\leq 10\)

Peut on améliorer cela ou vaut-il mieux ne pas mettre de maths dans les titres ?

Date de publication pour la disposition accordéon

On aimerait aussi avoir une date de publication dans la disposition  » accordéon  » pour programmer les solutions des défis (voir ici. https://images.math.cnrs.fr/wp-admin/post.php?post=15587&action=edit).
A l’heure actuelle, on peut commenter les titres et contenus de ces blocs mais ils apparaissent (bloc gris) même si ils sont vides (voir ci-dessous). On aimerait qu’ils n’apparaissent pas

Tableau

Y aura t-il une fonctionnalité tableau ?
Pour pouvoir directement obtenir des tables de ce genre