Hydrodynamique

• Systèmes dynamiques
• Physique

• Ressources pédagogiques

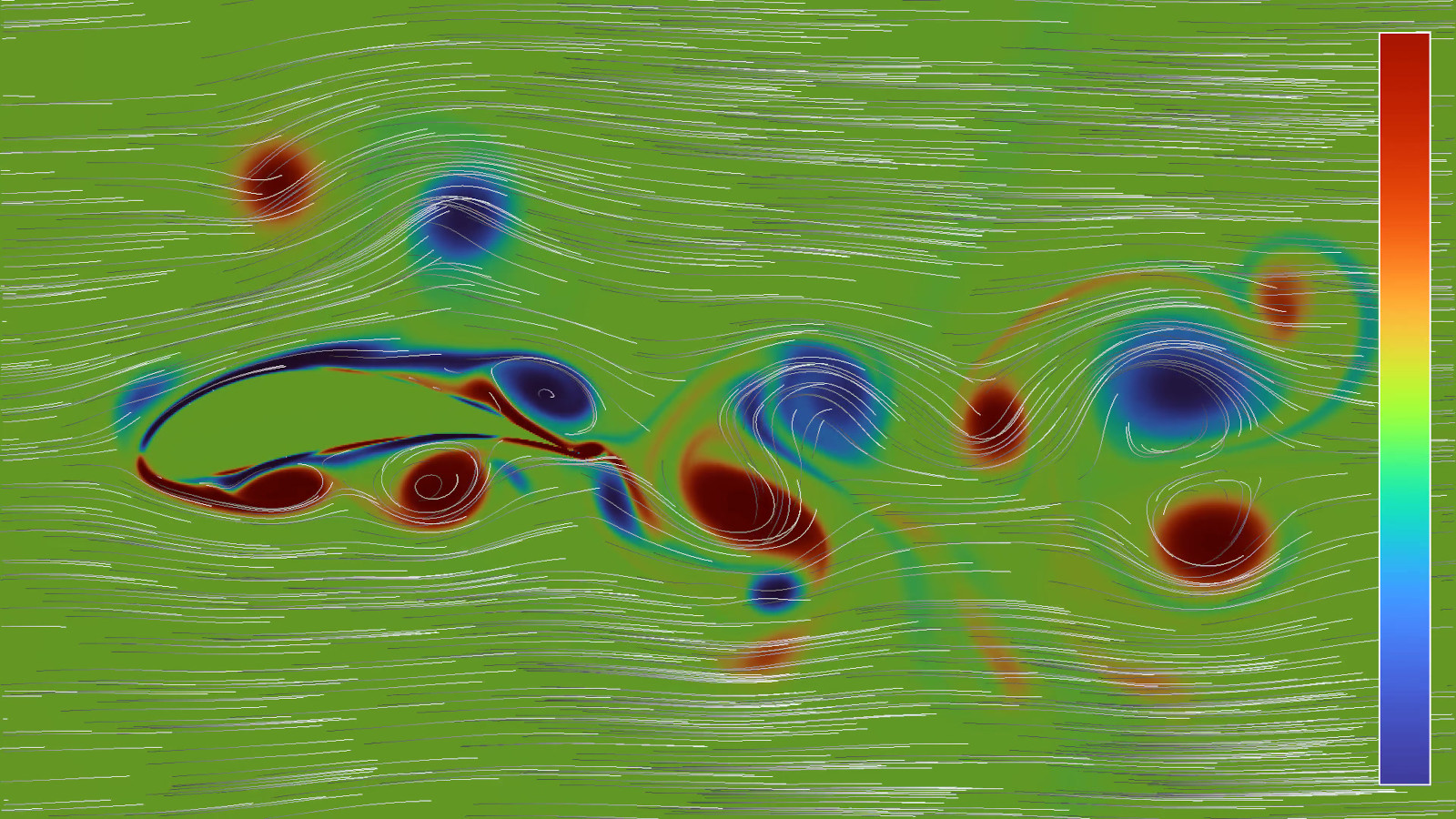
Vortex de Von Kármán

Les vortex de Von Kármán sont des tourbillons qui se forment lorsqu’un fluide et un obstacle se rencontrent avec une vitesse relative suffisamment grande. La vidéo montre une simulation des équations d’Euler compressibles avec conditions aux bords périodiques. Un obstacle en forme d’aile d’avion est représenté par une force répulsive fortement localisée. La vitesse relative du fluide est imposée aux bords gauche et droit du rectangle, et augmente au cours du temps. Cela permet de voir des vortex se développer lorsque la vitesse est assez grande. La vidéo, en quatre parties, montre d’abord la vorticité du fluide, qui mesure sa quantité de rotation, puis sa densité, qui est directement liée à sa pression. Les deux dernières parties montrent la même évolution en accéléré, avec un facteur d’accélération de 3. Le champ de vitesse du fluide est matérialisé par des traceurs passifs, qui se comportent comme des particules dont la vitesse est égale à celle du fluide.

Représentation 3D d'un écoulement de cisaillement sur le tore

Cette simulation des équations d’Euler incompressibles montre un écoulement de cisaillement dans le plan, la troisième dimension représentant la vorticité du fluide, qui mesure sa quantité de rotation. L’état initial est formé de plusieurs bandes parallèles, dans lesquelles la vitesse est différente. Cette configuration est répétée périodiquement dans le plan, et perturbée légèrement dans la direction perpendiculaire, afin de la rendre instable. Cette vidéo en deux parties montre la même évolution avec deux palettes de couleur et deux variables verticales différentes. Les deux parties montrent la vorticité du fluide, mais sur une échelle linéaire dans la première partie et sur une échelle logarithmique dans la seconde partie.

Écoulement de cisaillement sur le tore

Cette simulation des équations d’Euler incompressibles montre un écoulement de cisaillement. Les bords gauche et droite de la région rectangulaire sont identifiés, ainsi que les bords supérieur et inférieur, ce qui correspond topologiquement à un tore. L’état initial est formé de plusieurs bandes horizontales, dans lesquelles la vitesse est différente. Cette configuration est perturbée légèrement dans la direction verticale, afin de la rendre instable. Le phénomène observé d’inversion de la position des bandes, passant d’horizontales à verticales, est peut-être causé par les dimensions du rectangle. En partant avec des bandes verticales, ou dans un domaine carré, il n’est pas sûr que cette inversion se produirait.

Cette vidéo en deux parties montre la même évolution avec deux palettes de couleur différentes. Les deux parties montrent la vorticité du fluide, qui mesure sa quantité de rotation, mais sur une échelle linéaire dans la première partie, alors que dans la seconde partie l’échelle est logarithmique.