Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
10h38
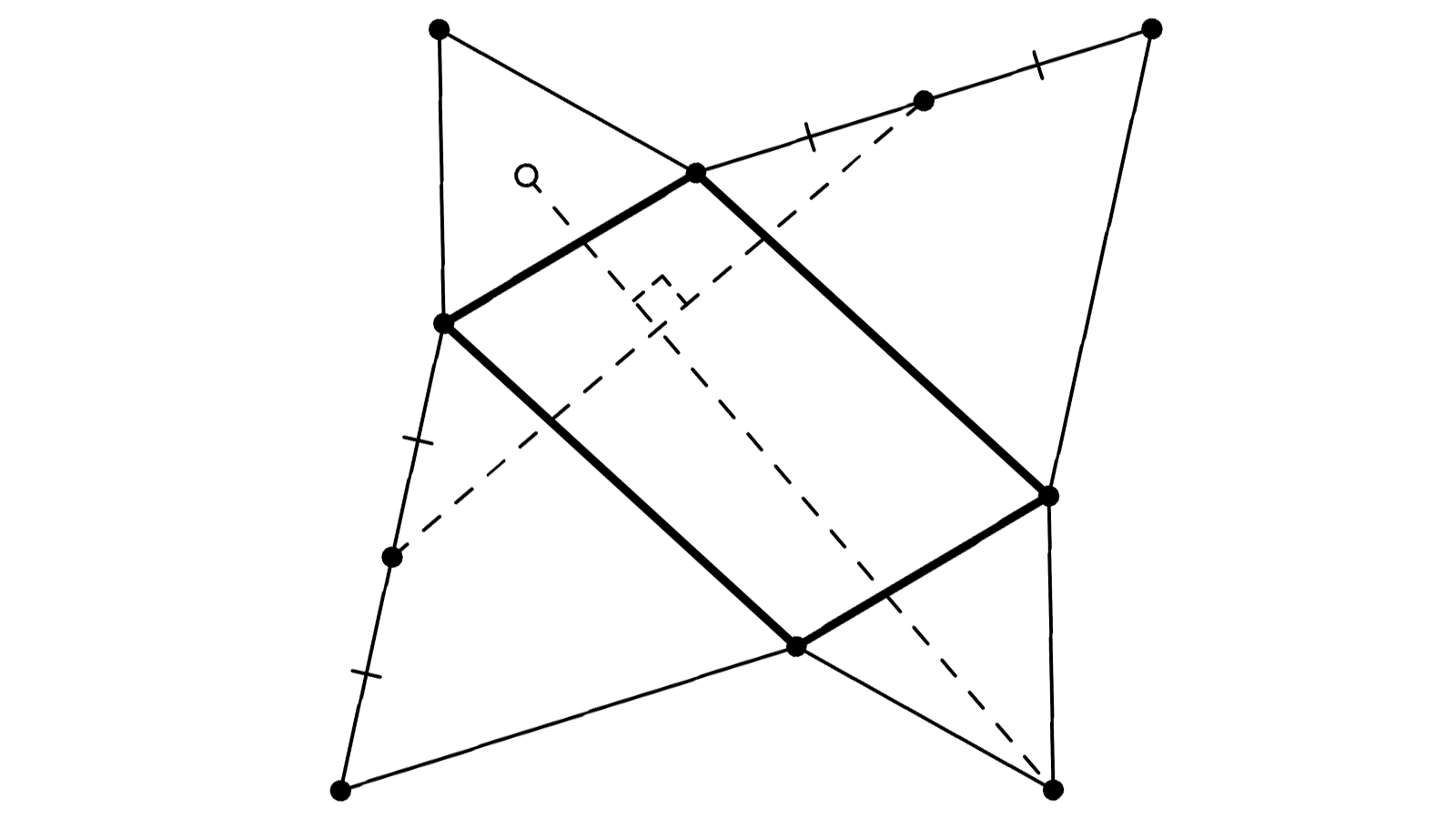
ABCD est parallélogramme. ABE, BCF, CDG et DAH sont des triangles équilatéraux.
I et J sont les milieux de [AE] et [DG]. K est le centre de DAH.
Il s’agit de démontrer que (IJ) et (FK) sont perpendiculaires.
Dans le parallélogramme on a les égalités d’angles (AD,AB) = (BA,BC) = (CB,CD) = (DC,DA) = a
(AK,AI) = (AK,AD) + (AD,AB) + (AB,AI) = π/6 + a +π/3 = a +π/2
(DJ,DK) = (DJ,DC) + (DC,DA) + (DA,DK) = a +π/2
Les triangles AIK et DJK sont égaux puisque :
ils ont un angle égal (AK,AI) =(DJ,DK) et deux côtés égaux AK = DK et Ai = DJ
D’où KI = KJ et K est sur la médiatrice de [IJ]
On trouve aussi (BI,BF) = (CJ,CF) = a + π/2, triangle BIF = triangle CJF et FI =FJ
D’où (FK) est la médiatrice de [IF]
21h05
Il y a une palanquée de triangles équilatéraux dans la figure. FIJ en premier lieu, et puis HBG, FED, etc. Des figures intéressantes cachées