Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
18h40
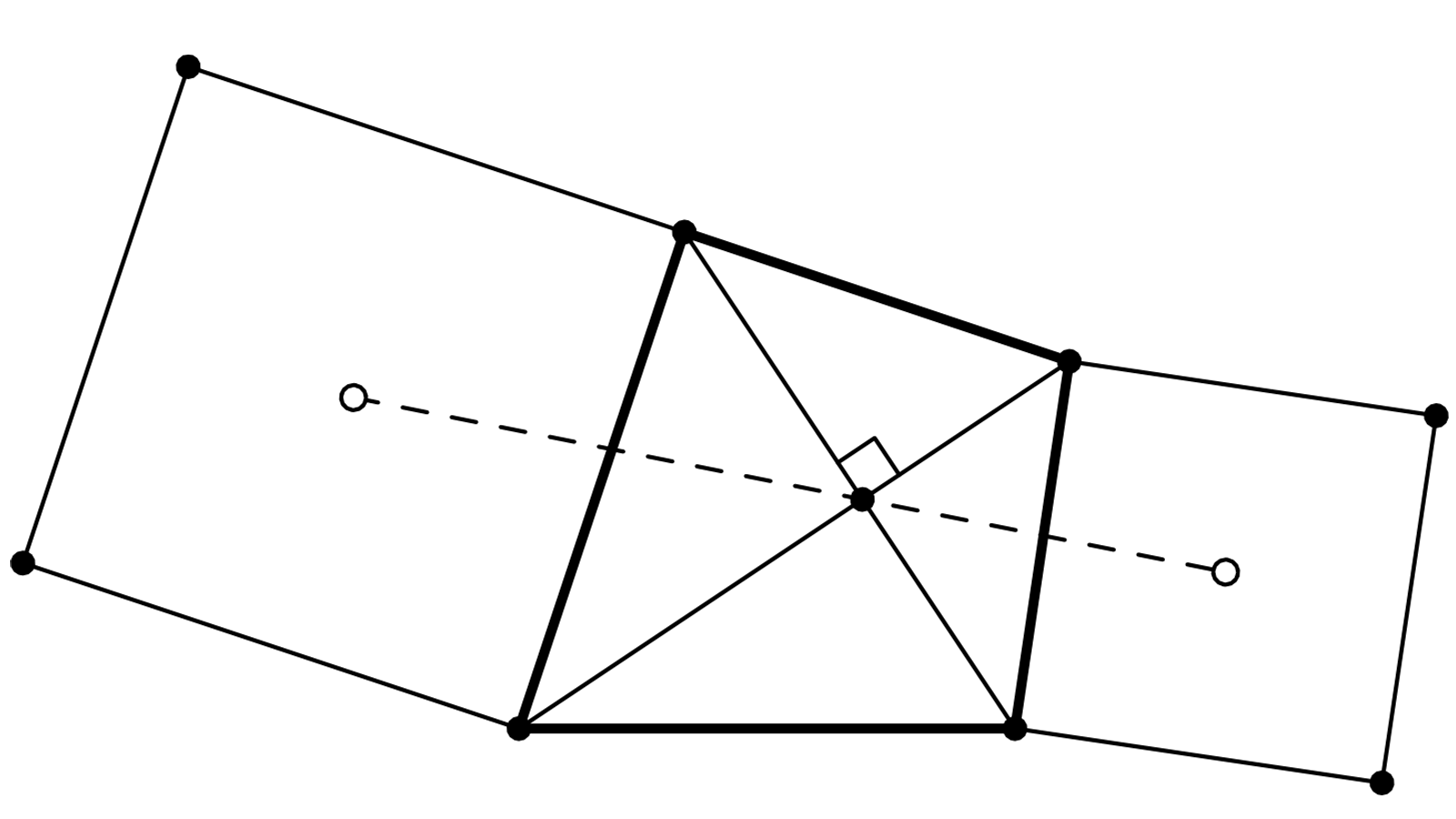
ABCD est un quadrilatère dont les diagonales sont perpendiculaires et se coupent en M.
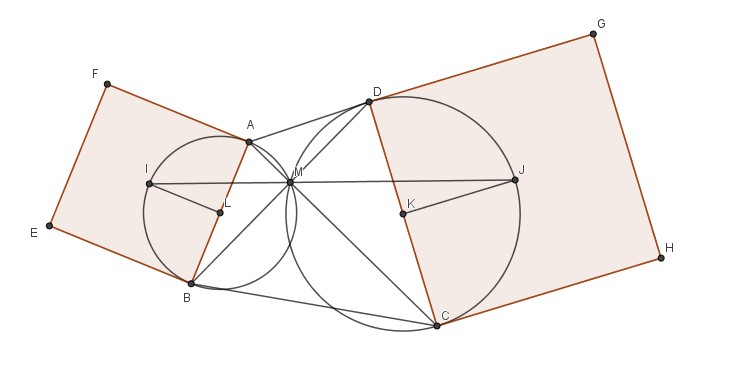
A l’extérieur de ABCD on trace les carrés ABEF et CDGH dont les centres sont I et J.
Il faut démontrer l’alignement I, M et J.
Soit L et K les milieux de [AB] et [CD].
AIB et CJD sont des triangles rectangles isocèles donc les cercles de diamètres [AB] et [CD] passe par I et M pour l’un, J et M pour l’autre.
Il vient (MA,MI) (angle inscrit) = (LA,LI)/2 (angle au centre) = π/4
De même (MC,MJ) = (KI,KC)/2 = π/4
D’où (AC,MI) = (AC,MJ) : (MI) = MJ) et M, I et J sont alignés.