

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
10h00
Il suffit de partager les carrés en 2 triangles, puis d’appliquer deux fois les résultats du 4.12.9. https://images.math.cnrs.fr/4-12-9.html
13h54
Exactement ! Et rappelons que (comme dans 4.12.9) on peut placer le carré « tireté » non plus à la moitié, mais à une fraction quelconque des lignes qui joignent les carrés extrêmes, conformément à la remarque de Sidonie.
14h13
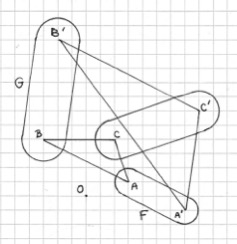
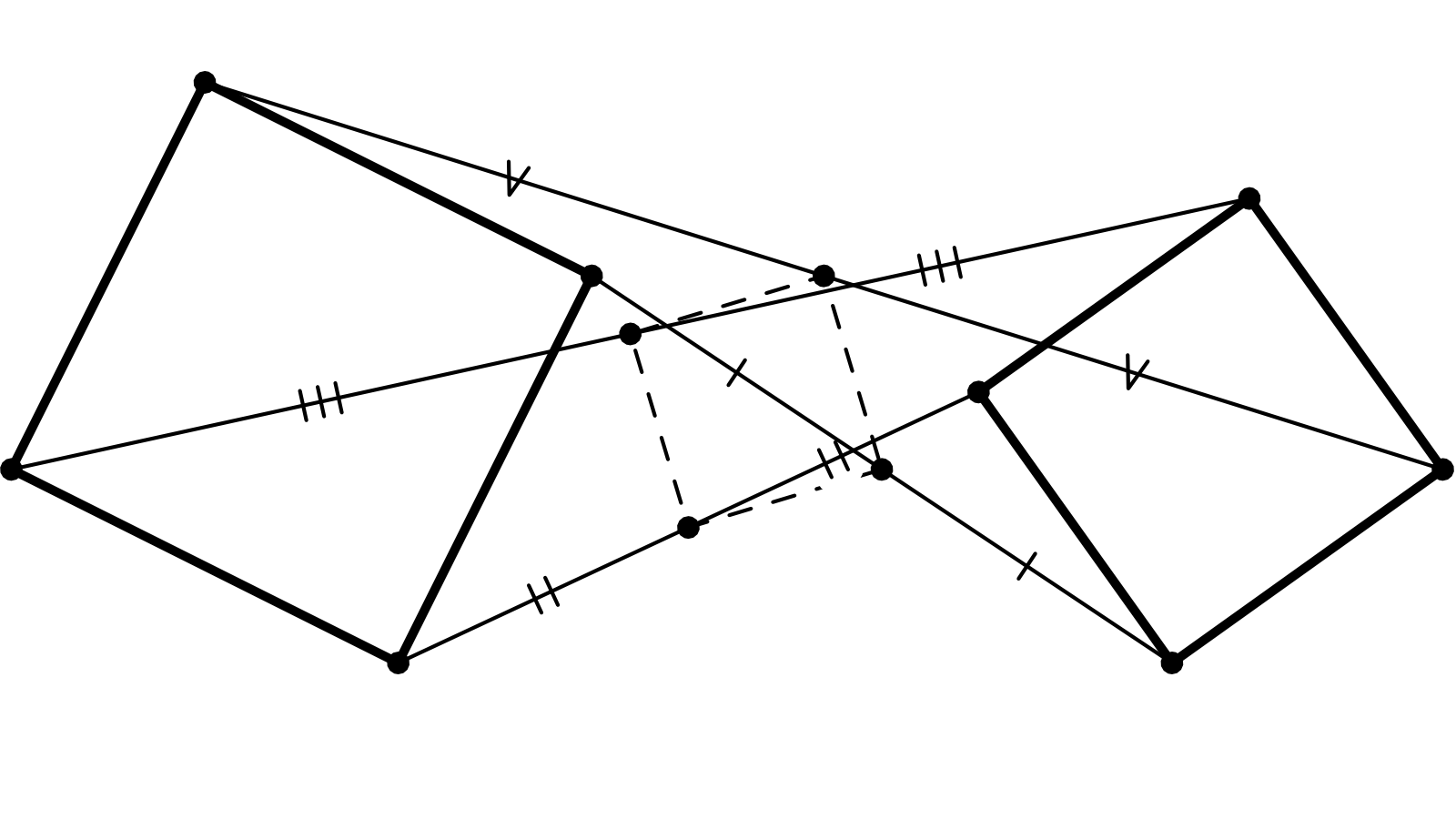
Il est possible de généraliser encore un peu : « une fraction quelconque des lignes » peut être remplacée par des points hors\(\,\) des lignes, comme ceci.
On part de deux figures planes F et G, que l’on suppose directement semblables [1] (en 4.12.9 c’étaient deux triangles quelconques, ici ce sont deux carrés ; c’est évidemment sans importance). Appelons S la similitude qui envoie F sur G ; fixons des points A dans F et B dans G tels que B = S(A) ainsi qu’un point C dans le plan. Pour tout point A’ de la figure F, en appelant B’ le point S(A’), il existe un unique point C’ du plan tel que le triangle A’B’C’ soit directement semblable à ABC. Et lorsque A’ décrit la figure F (et donc B’ la figure G), la figure décrite par C’ est directement semblable à F et G. [2]
(Dans le cas que vous considérez, C est sur la droite AB et les triangles A’B’C’ sont aplatis ; et sur la figure proposée ainsi qu’en 4.12.9, C est en outre au milieu de AB.)
Pour établir cette propriété, introduisons le centre O de la similitude S, [3] et rappelons que les similitudes de même centre O peuvent se composer dans n’importe quel ordre, puisque l’on ajoute les angles de similitude et que l’on multiplie les rapports de similitude. Pour A’ donné, il existe une unique similitude U de centre O et telle que A’ = U(A). Puisque S(U(A)) = S(A’) = B’, on a aussi B’ = U(S(A)) = U(B), et U envoie à la fois A sur A’ et B sur B’. Elle envoie alors le triangle ABC sur un triangle A’B’C’’ directement semblable à ABC et donc aussi à A’B’C’, ce qui fait que les points C’ et C’’ doivent être les mêmes, c’est-à-dire que U(C) = C’.
En appelant maintenant T la similitude de centre O telle que C = T(A), qui, elle, ne dépend pas du choix de A’, on peut pour tout A’ écrire U(T(A)) = C’, d’où C’ = T(U(A)) = T(A’) ; ainsi, lorsque A’ parcourt F, C’ décrit la figure T(F) directement semblable à F.
(1) On a entre les deux une bijection qui tourne tous les vecteurs d’un même angle, et qui multiplie toutes les distances par une même quantité — cette deuxième exigence résultant automatiquement de la première dès que les figures comportent trois points non alignés.
(2) Elle est exceptionnellement réduite à un point si C a été pris au centre de similitude de S.
(3)Dans le cas dégénéré où S est réduite à une translation, le centre n’existe pas, mais le résultat subsiste alors directement.