

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
22h43
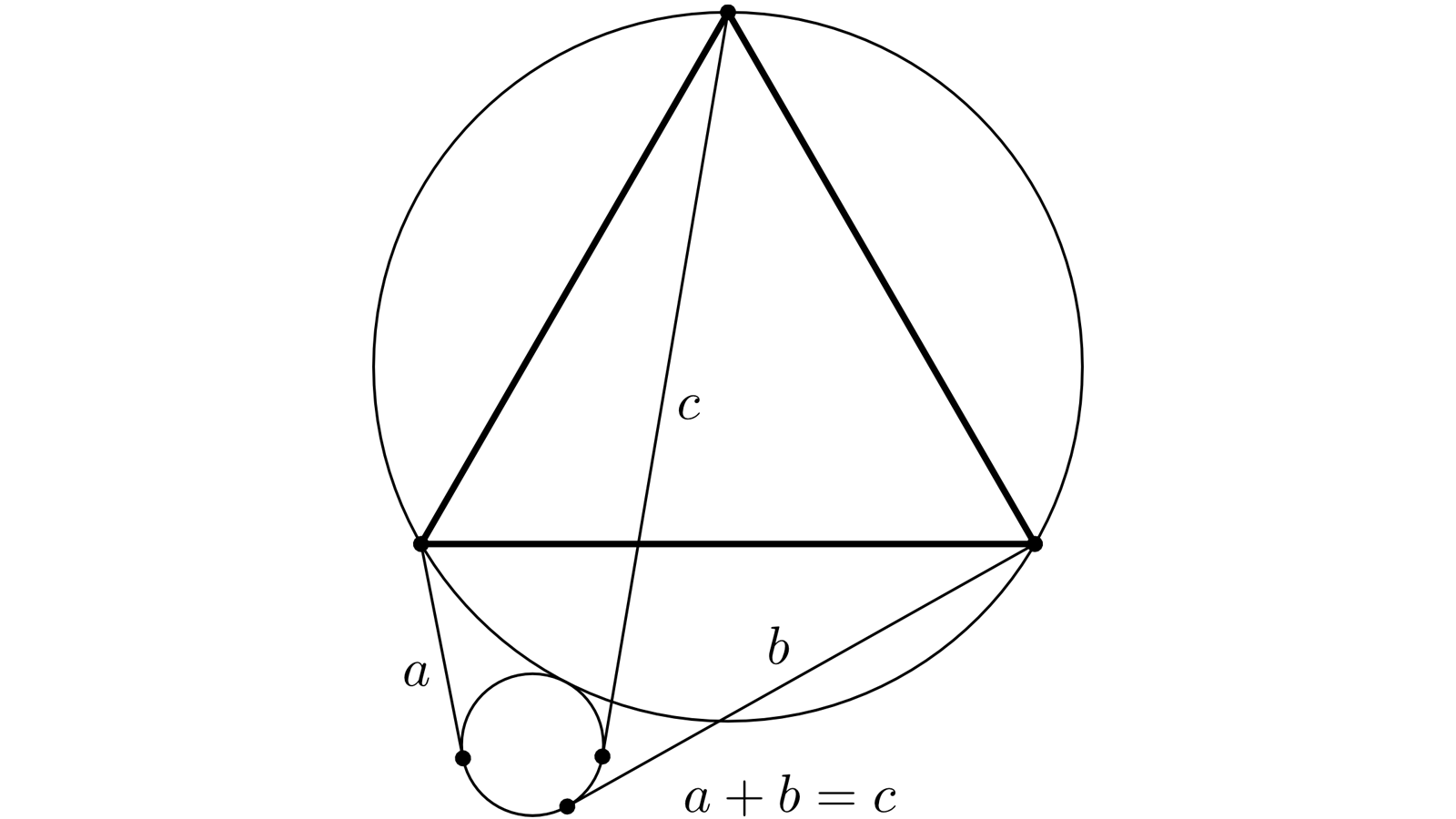
Je démontre un résultat plus général qui appliqué à la figure donne le résultat. Le nom des cercles est le même que leurs centre en minuscule.
Description : Deux cercles (a) et (c) sont tangents en B. D et E appartiennent à (a). (DF) et (EG) sont tangents à (c).
Conclusion : DP/DB = EG/EB
(BH) est la tangente commune à(a) et (b) et H appartient à (DE). (h) est le cercle qui passe par B, (d) passe par F et (e) passe par G. I et J sont les intersections entre (d) et(h).
Par construction (h), (d) et(e) sont orthogonaux à (c), de plus H, D et E sont alignés : ils forment un faisceau ce qui prouve que (e) passe aussi par I et J, d’où DI = DP et EI = EG
K et L non marqués sont les intersections de (DE) et (h). Par construction ils partagent harmoniquement D et E. Le cercle (h) est le lieu des points M tels que MD/ME est constant.
Donc ID/IE = BD/BE . DP/DB = DI/DB = IE/BE = GE/BE …CQFD…
Appliqué à la figure : les 3 longueurs a, b et c de cette semaine sont proportionnelles à a,b et c de la semaine dernière.
20h52
Très jolie preuve ! (j’ai l’impression que F et P ne font qu’un ?)
12h18
Tout à fait : ma vue fort défaillante m’a fait confondre F et P, confusion classique dans les examens oculaires.
15h46
Me permettrez-vous de proposer une autre démonstration de votre joli résultat ?
On peut l’énoncer ainsi : Soient deux cercles\(\,\) (a) et\(\,\) (c), tangents (extérieurement ou intérieurement) en un point\(\,\) \(B\). Si un point variable\(\,\) \(D\) décrit le cercle \(\,\)(a), sa puissance par rapport à\(\,\) (c) reste proportionnelle à\(\,\) \(DB^2\). Lorsque (a) est à l’extérieur de (c) (même si les cercles sont tangents intérieurement), cette puissance est le carré d’une tangente \(DF\) menée de \(D\) à (c), et l’on a alors proportionnalité entre \(DF\) et \(DB\).
En effet, le point de contact \(B\) est le centre d’une homothétie envoyant (a) sur (c), de sorte que le point \(D’\) où la droite \(DB\) recoupe (c) vérifie \(\,\overline{\!BD’\!\!}\,\,=k\,\,\overline{\!BD\!}\,\), où \(k\) est le rapport d’homothétie (c’est le rapport des rayons affecté d’un signe \(\pm\) selon la nature du contact ; mais peu importe). Ceci peut se réécrire \(\,\overline{\!DD’\!\!}\,\,=(1{-}k)\,\,\overline{\!DB\!}\,\) ; multiplier les deux membres par \(\,\overline{\!DB\!}\,\) fournit la valeur \((1{-}k)\,\,DB^2\) pour la puissance \(\,\overline{\!DB\!}\,\,\,\,\overline{\!DD’\!\!}\,\,\).
\({}\)
Remarque : Lorsque (c) est intérieur à (a), la propriété illustrée ici est un cas particulier (avec trois rayons nuls) de la Figure sans Paroles 6.1.10 ; cette dernière reste d’ailleurs vraie (votre démonstration s’étendant à ce cas) lorsque les quatre cercles auxiliaires y sont tangents extérieurement\(\,\) au cercle principal.
10h18
Comme souvent, vous généralisez et simplifiez. Je tiens tout de même vous remercier pour m’avoir rappelé les faisceaux de cercles à l’occasion d’une figure sur les quadrilatères complets. Je n’ai pas assez d’internet pour la retrouver.
11h34
Peut-être évoquez-vous la Figure sans Paroles 3.10 ?