Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
15h36
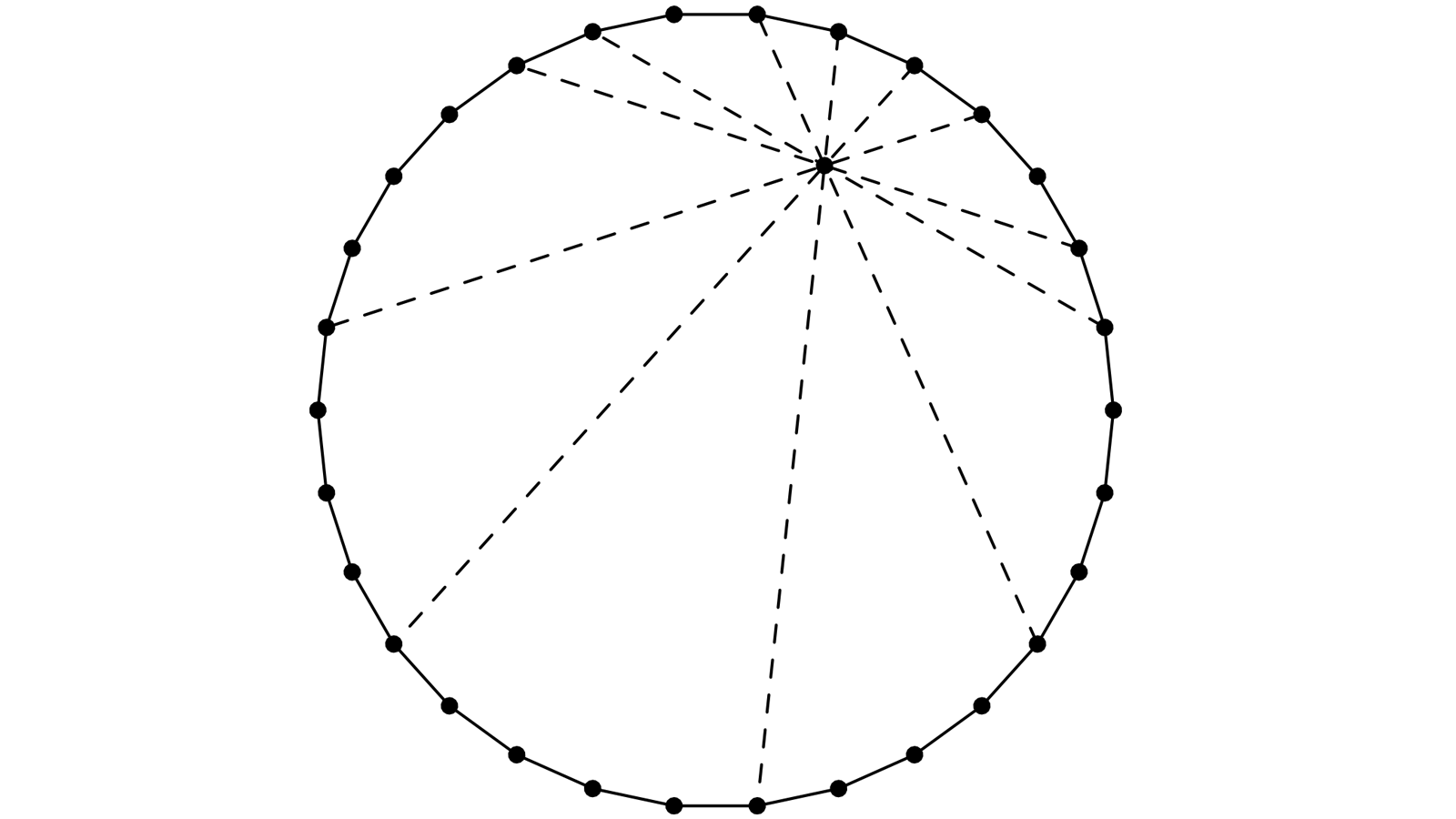
Tout augmente ! Même le degré de nos polygones. Un 30-gone << triancontagone >>.
Un point A, arbitraire. Puis, en tournant dans le sens << horaire >> B:A+4, C:B+1, D:C+2, E:D+1, F’:E+1, A’:F’+1, A’:B’+2, C’:B’+1, D’:C’+4, E’:D’+4, F=E’+5 (on vérifie, A:F+4).
Les diagonales AA’, BB’, CC’, DD’, EE’, FF’ sont concourantes.
.
On utilisera encore θ=2π/30 ; O est le centre du cercle circonscrit, et je prends pour P l’intersection (AA′)−(DD′).
Les diagonales AA′ et DD′ ont même longueur. Si je nomme X le milieu de l’arc DA′ du cercle circonscrit (ou de l’arc EF′), il est clair que (OX) est un diamètre du cercle circonscrit, et que DD′ et AA′ sont symétriques par rapport à ce diamètre : P est situé sur ce diamètre (ADA’D’ est un trapèze isocèle).
Il en est de même pour CC′ et BB′ d’une part, pour EE′ et FF′ d’autre part (des trapèzes isocèles admettant OX comme axe de symétrie).
Ainsi, les couples (AA′−DD′), (EE′−FF′), (BB′,CC′), ont leurs intersections sur OP — mais il reste à montrer que ces intersections sont confondues avec le point P.
La médiatrice de la diagonale AA′ est un diamètre passant par C (puisque C est le milieu de l’arc AA′). Et inversement, AA′ est médiatrice de OC (A′CO, comme AOC, sont des triangles équilatéraux). PCO est donc isocèle et l’angle (CO,CP)=(OP,OC) vaut 42° (ou 7θ/2). C’est aussi la valeur de (CO,CC′) : C,P,C′ sont alignés, et donc P est aussi l’intersection de CC′ et BB′.
L’examen des angles montre que (PB,PA)=3θ=(AA′,AB) : B est sur la médiatrice de AP, qui est donc aussi la bissectrice de (BA,BB′) : c’est la droite (BE′), et donc (E′B,E′A)=(E′P,E′B)=2θ=(E′E,E′B) : E′,P et E sont alignés, ce qui fait de P l’intersection de EE′ et FF′.