Commentaires
Écrire un commentaire
Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
13h34
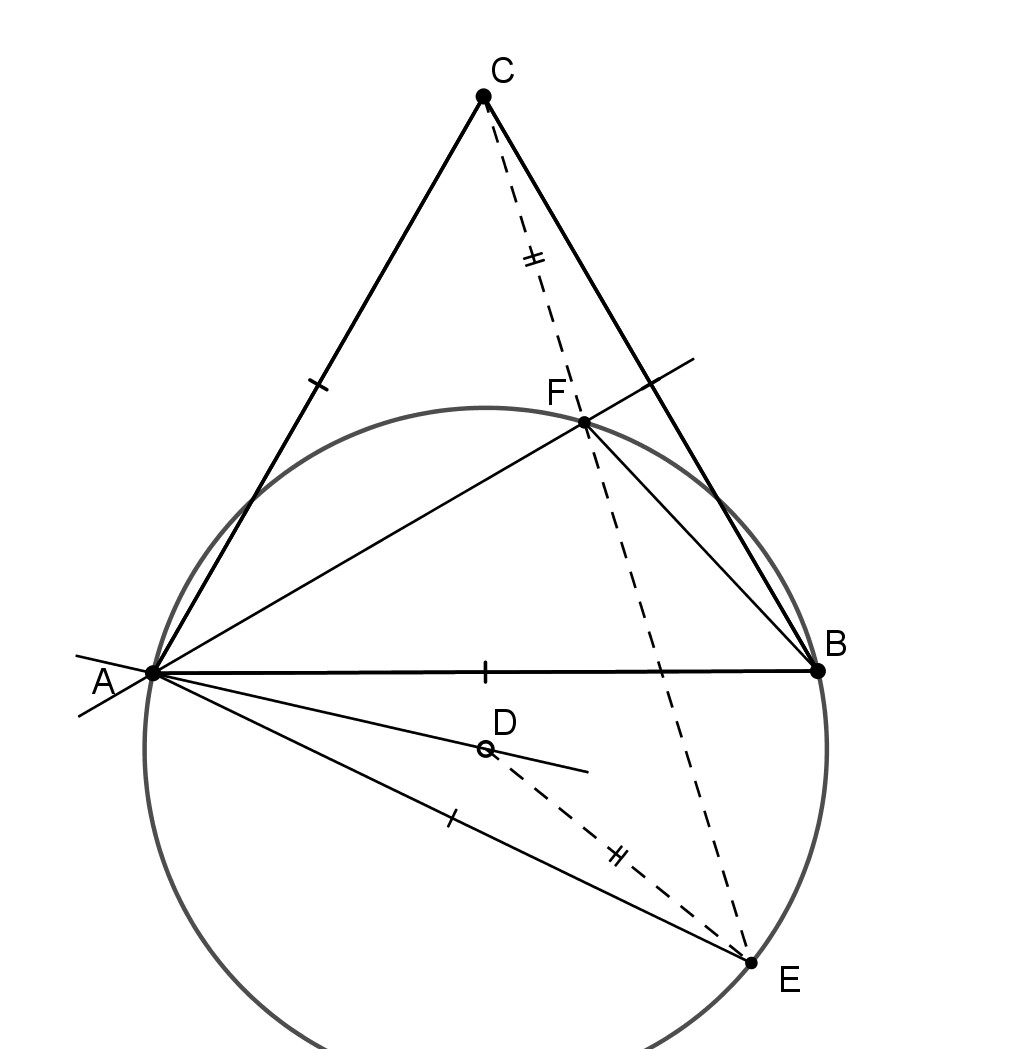
Un triangle ABC équilatéral. Depuis un point D situé sur la hauteur issue de C, un cercle passant par A et B. Un point E sur ce cercle tel que AE=AC. On note F l’intersection du cercle et de (CE).
Les segments [CF] et [DE] ont même longueur.
.
Dans le cercle (D), (EC,EA)=(BF,BA). Comme AEC est isocèle, (CA,CE)=(EC,EA)=(BF,BA).
Par différence, puisque les angles en B et C du triangle ABC sont égaux, (CE,CB) et (BC,BF) sont égaux. FBC est donc isocèle et les segments FC et FB ont même longueur.
De plus les triangles AFC et AFB, dont les côtés sont égaux, sont égaux : (AB,AF)=(AF,AC)=30°, et AF est la bissectrice en A du triangle.
(DB,DF)=60° (angle au centre) et donc DBF est équilatéral : FB et DB ont même longueur ! FC, FB DE ont même longueur.
15h37
Autre solution (pas plus simple) : Les cercles se nomment comme leurs centres en minuscules.
Dans (a) : (EB,EC) = 30° (angle inscrit) car (AB,AC) = 60° (angle au centre)
Dans (d) : (DF,DB) = 60° (angle au centre ) car (EF,EB) = 30° (angle au centre) d’où DFB équilatéral.
Le cercle (f) passant par B passe aussi par D et aussi par C puisque (FD,FB) = 60° et (CD,CB) = 30°
D’où FC = FD (CQFD)
Petit plus (f) passe aussi par G autre intersection entre (AC) et (d) une ribambelle qui s’applique même si ABC n’est qu’isocèle en C : (GC,GB)= (GA,GB) = moitié(DA,DB) = (DC,DB).
Et (AB,AF) = 30° montre que F est sur la médiatrice de [BC]
20h50
Oui ! Joli argument !