

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
12h42
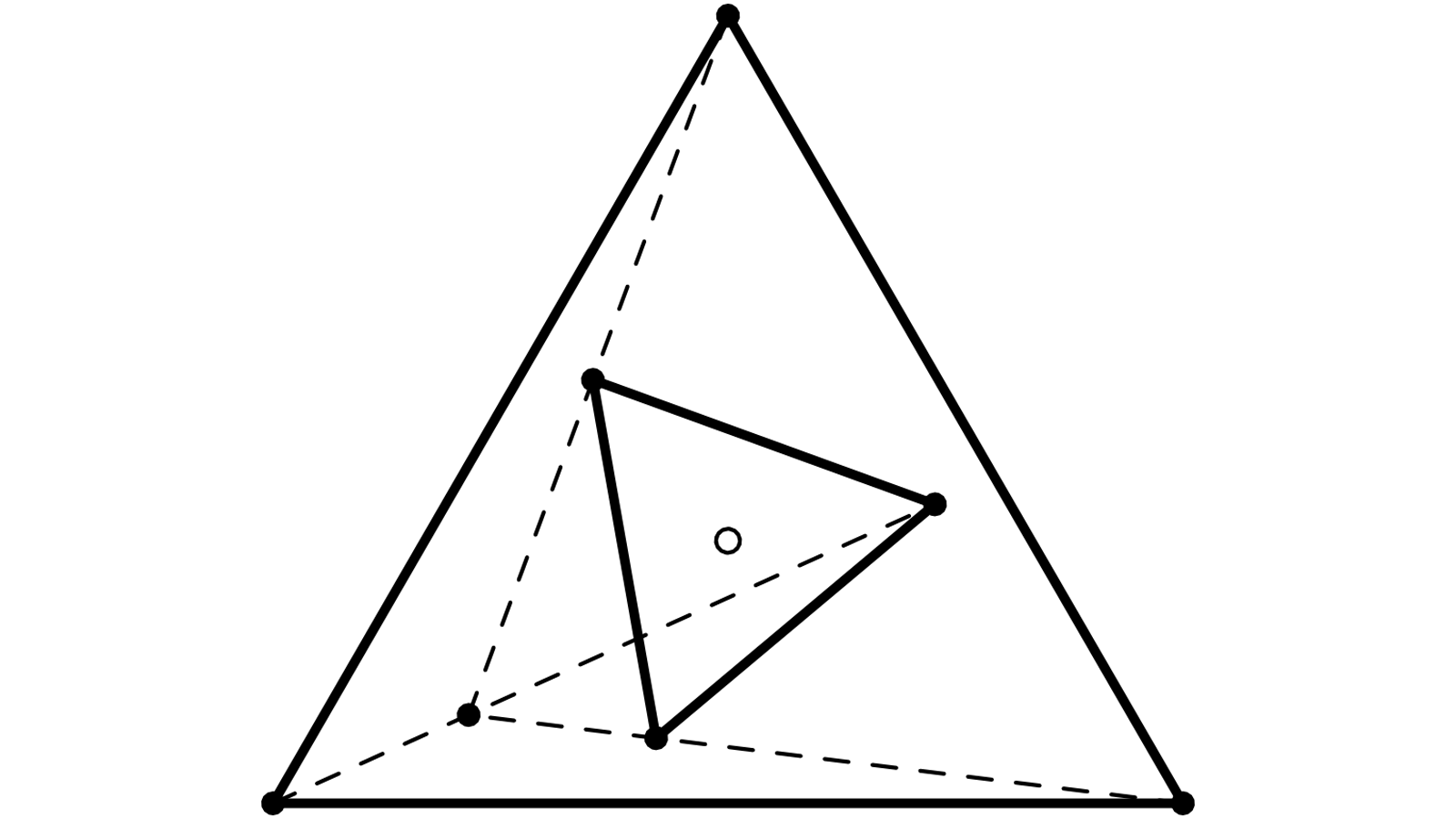
Je me donne un triangle équilatéral ABC. Je note O son centre (centre du cercle circonscrit).
Un second triangle A’B’C’, équilatéral et de même centre O, lui est intérieur.
Les droites AB’, BA’ et CC’ sont concourantes.
.
Je prolonge mes droites concourantes : AB’ coupe BC en D ; BA’ coupe AC en E ; CC’ coupe AB en F.
Etablir la concourance pourra se faire via le théorème de Céva :
(FA/FB)*(DB/DC)*(EC/EA)=-1 (1)
(avec les chapeaux sur les segments !)
.
Je trace BB’, qui vient couper AC en J, puis CB’, qui vient couper AB en K.
De toute évidence, AD, BJ et CK sont concourantes, et donc
(DB/DC)*(JC/JA)*(KA/KB)=-1 (2)
(avec les mêmes chapeaux)
.
Mais la figure présente une symétrie de rotation : toute rotation de $2\pi/3$ autour de O la laisse invariante, ce qui signifie que BK et AE ont même longueur, de même que CJ et AF.
En substituant ces égalités, on transforme les égalités, (2) devient (1).
9h44
Question subsidiaire. Si je fais tourner le triangle A’B’C’ autour de O — laissant ABC fixe, le point d’intersection de mes trois droites décrit une figure curieuse, que peut-on en dire ?
16h29
Je me permets de reprendre votre idée en l’aménageant autrement.
D,E et F deviennent les intersections entre (AB)(B’C’), (BC)(A’B’) et (AC)(A’C’).
(B’C’) coupe (AC) en G et (BC) en H.
Vision multiplicative de Ménélaus et toujours sans chapeau :
D,G et H alignés donnent ADxBHxCG = AGxBDxCH (1)
Les rotations que vous décrivez : BH = CF, CG = BE, AG = CE et CH = AF (2)
En combinant (1) et (2) il vient ADxCFxBE = CExBDxAF ce qui prouve que D,E et F sont alignés.
Si on considère les triangles ABC et A’B’C’ D, E et F sont les intersections de leurs côtés 2 à 2 et en appliquant le Th de Desargues il vient (AB’), (BA’) et (CC’) concourantes.
21h26
imparable !
Ca contribue à ajouter des droites à la figure — et à l’orienter vers des arguments « projectifs » (l’inconnu pour moi).
La question qui me taraudait m’inclinait plutôt à essayer de d’introduire des rotations (la trajectoire que je mentionne me fait penser à une sorte de cycloide, épicycloide, …)
(voire hypo- ou hippocycloide, j’ai cru entrevoir une tête d’hippopotame)
14h11
Petite surprise, une recherche qui n’avait pas aboutie donne un curieux résultat.
La symétrie d’ordre 3 génère moult angles égaux et de là pas mal de cocyclité. 3 d’entre les cercles, AOA’, BOB’ et COC’, qui passent chacun par 2 autres points d’intersection (ce qui se démontre assez facilement), forment un faisceau et se recoupent en un autre point. C’est le but de ma démonstration.
Les centres de ces cercles sont les intersections des médiatrices de OA, OB et OC (en rouge sur la figure) avec les médiatrices de OA’, OB’ et OC’ (en bleu)
On obtient les triangles équilatéraux DEF (rouge) et D’E’F’ (bleu) symétriques par rapport à O à ABC et A’B’C’.
D’où la concourance de (DD’), (EE’) et (FF’) ce qui nous place dans les hypothèses du théorème de Desargues et donc l’alignement des intersections entre les côtés 2 à 2 à savoir les centre des 3 cercles M, N et P qui prouve le faisceau et l’existence du 2ème point d’intersection