

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
11h05
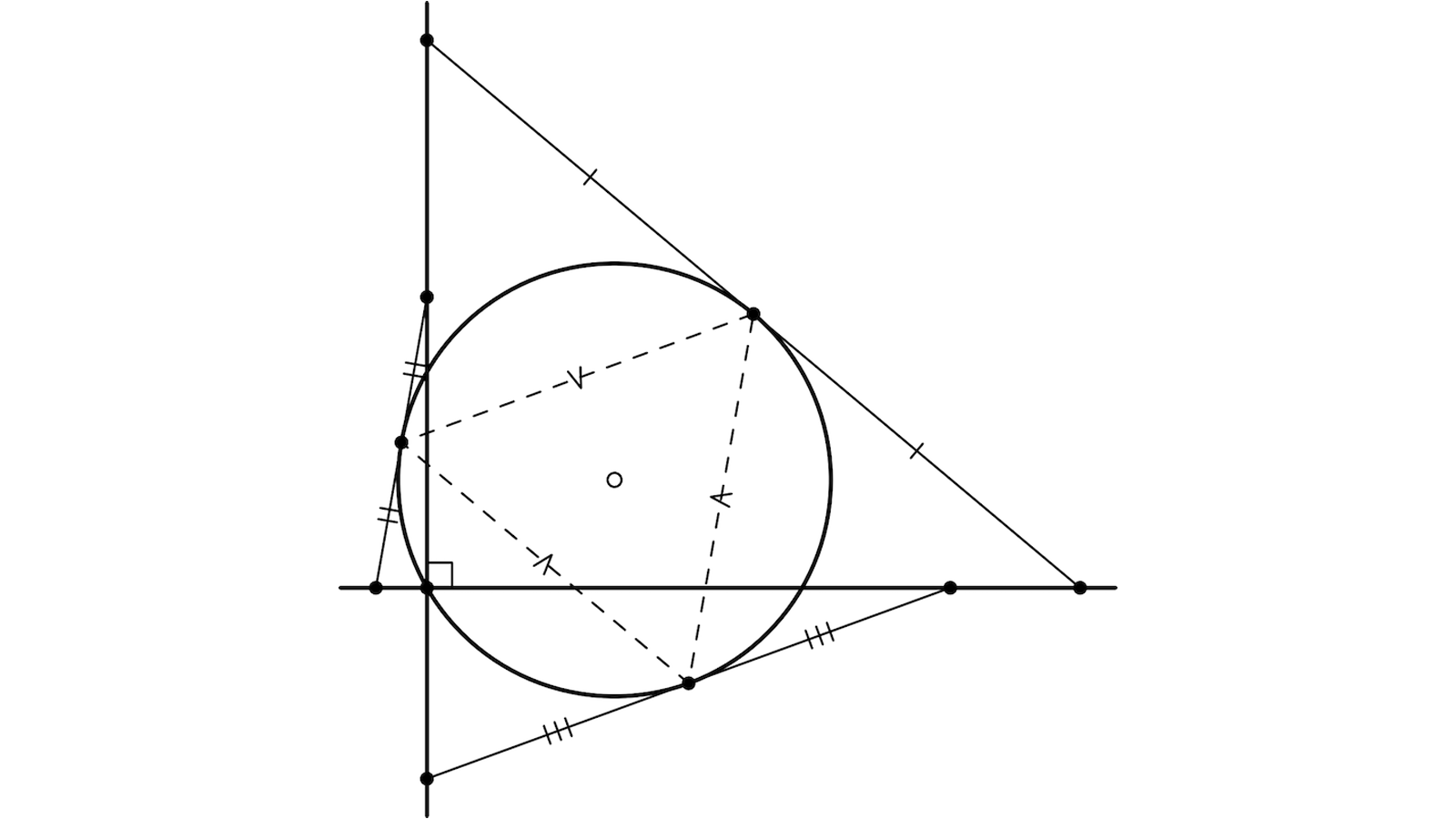
Curieuse figure. Un examen naïf donne ceci :
Deux droites orthogonales. Trois segments, appuyés comme des échelles sur ces droites, et trois points, milieux de chaque segment (je les appelle G, H, I).
Et alors, le triangle GHI est équilatéral.
.
De toute évidence, une construction selon ce schéma échouera !
.
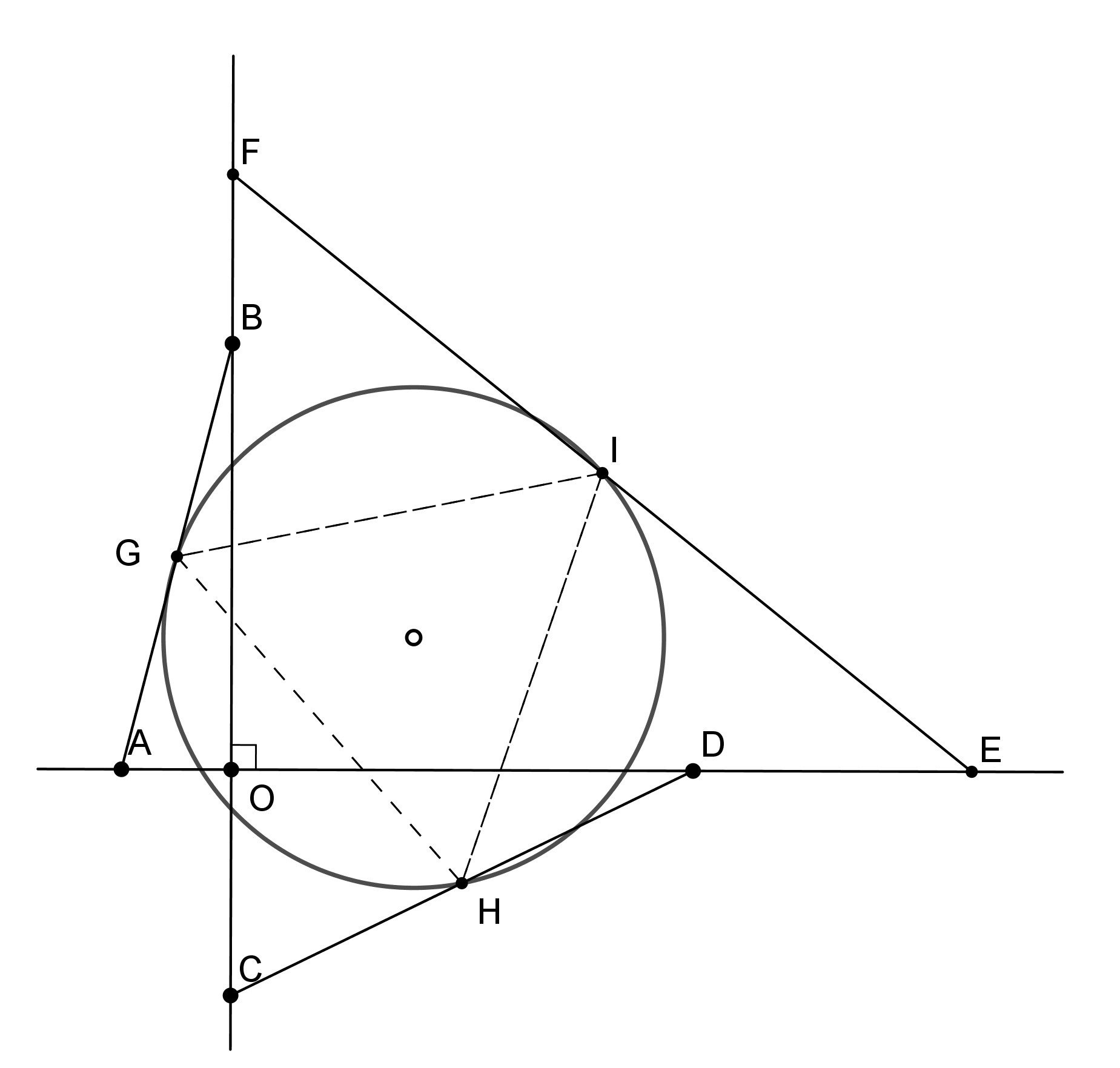
Je peux prendre le problème à l’envers :
.
je me donne deux droites orthogonales, deux segments AB et CD appuyés sur mes droites. Je note G et H les milieux de AB et CD.
Prenant GH comme base, je construis GHI, triangle équilatéral.
Depuis I, le segment EF, dont I est milieu (je le construis simplement, remarquant que l’angle droit en O fait de EF le diamètre d’un cercle de centre I passant par O).
Je peux alors exhiber une figure conforme au modèle 8.1.12.
.
Que faire alors, que rajouter pour aboutir à une énigme convenable ?
Document joint :
15h52
La question me semble celle-ci. Étant donnés deux axes perpendiculaires et un cercle passant par leur intersection, les points du cercle qui se trouvent au milieu du segment découpé sur la tangente en ce point par les deux axes sont au nombre de trois, et sont équidistants les uns des autres.
Il y a peut-être une attaque géométrique à ce problème, mais le calcul en coordonnées est si élémentaire que je ne vois pas de raison d’y renoncer.
En prenant des coordonnées rectangulaires selon les deux axes donnés, si vous appelez r le rayon du cercle et rcosα et rsinα les coordonnées de son centre, un point quelconque du cercle aura pour abscisse r(cosα+cosθ) et pour ordonnée r(sinα+sinθ). La tangente au cercle en ce point a pour équation
(x−r(cosα+cosθ))cosθ+(y−r(sinα+sinθ))sinθ=0,
et la propriété que doit satisfaire θ pour que le point soit au milieu du segment de tangente se réduit donc à
(cosα+cosθ)cosθ+(sinα+sinθ)sinθ=0,
c’est-à-dire finalement à cos(θ+α)+cos(2θ)=0. Les solutions sont premièrement θ+α=π+2θ à 2kπ près, c’est le cas dégénéré où le point est à l’intersection des axes ; et deuxièmement θ+α=π−2θ à 2kπ près, c’est-à-dire 3θ=π−α, ce qui donne les trois points cherchés.
16h34
Il commence à y avoir un sérieux problème informatique sur ce blog : j’ai pu poster un commentaire le 26 sans voir la réponse du précédent, publiée par Reine le 23 !
D’autre part, je recevais autrefois un mail, m’informant qu’un commentaire, justement, était posté en réponse à une publication que je pouvais faire. Ce n’est plus le cas, de sorte qu’on découvre ces réponses, au hasard d’un parcours…
Cela commence à devenir difficile à utiliser !
Alors, s’il vous plait, mesdames/messieurs webmasters, faites quelque chose !
10h12
Oui il y a de sérieux problèmes, désolée. Nous avons été piraté et les webmasters ont déjà passé beaucoup de temps pour régler un maximum de bugs. Ils sont bénévoles, on ne peut pas exiger d’eux qu’ils délaissent leur travail pour tout nous régler.
Le secrétariat de Rédaction.
17h12
Merci pour ces précisions, qui donnent effectivement un sens à la figure (et une solution !).
J’ai imaginé une version « épurée », ou « schématique », du résultat : si on prolonge les segments-échelles, on obtient un autre triangle équilatéral, et alors la propriété conduit à la figure suivante :
.
On prend deux droites, passant par un point A. D sera le centre d’un cercle, tangent à ces droites en B et C.
On se donne un point P sur le cercle, puis deux cercles, de centres B et C passant par P. Le cercle (B) va couper la droite en F et G, le cercle (C) coupera la sienne en H et J.
On a alors le résultat : J, P, F sont alignés (de même que G, P, H) si et seulement si l’angle en A mesure 60°.
Par construction, (PJ,PH)=(PF,PG)=90°. On a donc l’alignement J,P,F si et seulement si (PH,PF)=90° (H, P, G sont alignés en même temps).
Cela va se ramener à une (laborieuse) histoire d’angles. Je note w=(AB,AC). Alors (DC,DB)=180-w.
Je note u=(DP,DB). (BD,BP)=90-u/2, (BP,BF)=u/2, (FB,FP)=90-u/4 et (FP,FA)=90+u/4.
Le même calcul s’applique à (HA,HP), en remplaçant u par 180-w-u :
(HA,HP)=90+(180-w-u)/4.
Le calcul de (PH,PF), dans le quadrilatère AFPH, va donner
(PH,PF)=360-w-(90 + u/4 + 90 + 45 – w/4 – u/4), soit (PH,PF)=135-3w/4.
Angle qui vaut 90° ssi l’angle en A vaut 60°
11h47
Oui, c’est bien vu ! Vos arguments d’hier et du 26 mai sont bien plus parlants que mes bêtes calculs.
16h39
Peut-être, si on demande aux segments d’être tangents au cercle ? Pas évident que ce soit vérifié sur le dessin proposé — mais pourquoi pas ?
Dans ce cas, si O est le centre du cercle, (GH,GO)=30° donc (GA,GH)=60°, de même que (HG,HC), etc.
P étant l’intersection de (GA) et (HC), GHP est alors équilatéral (même chose pour les autres paires de segments).