

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas
d’en abuser ! Les formules mathématiques doivent être composées avec les balises
.
Par exemple, on pourra écrire que
sont les deux solutions complexes de l’équation
.
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.
10h20
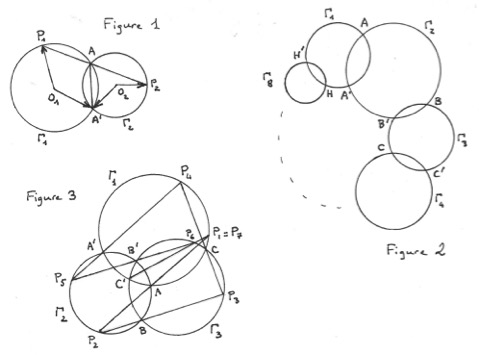
Cette figure est composée de briques élémentaires toutes du même type (figure 1 jointe). Étant donnés deux cercles \(\Gamma_1\) et \(\Gamma_2\) de centres \(O_1\) et \(O_2\) et ayant deux points communs \(A\) et \(A’\), on peut passer d’un point quelconque \(P_1\) de \(\Gamma_1\) à un point \(P_2\) de \(\Gamma_2\) « via le point \(A\) » en prenant \(P_2\) aligné avec \(A\) et \(P_1\). On a alors (angles orientés de vecteurs et de droites)\[(\vec{O_2A’},\,\vec{O_2P_2})=2\,(AA’,\,AP_2)=2\,(AA’,\,AP_1)=(\vec{O_1A’},\,\vec{O_1P_1})\;,\]d’où \({(\vec{O_1P_1},\,\vec{O_2P_2})=(\vec{O_1A’},\,\vec{O_2A’})}\). Ainsi, la position de \(P_2\) sur \(\Gamma_2\) se déduit de celle de \(P_1\) sur \(\Gamma_1\) par la rotation d’angle \((\vec{O_1A’},\,\vec{O_2A’})\).
Considérons maintenant (figure 2) une chaîne de quelques cercles, par exemple huit, \(\Gamma_1\), \(\Gamma_2\), …, \(\Gamma_8\), tels que \(\Gamma_1\) et \(\Gamma_2\) se rencontrent en deux points \(A\) et \(A’\), de même \(\Gamma_2\) et \(\Gamma_3\) en \(B\) et \(B’\), etc., jusqu’à \(\Gamma_8\) qui croise \(\Gamma_1\) en \(H\) et \(H’\). Partant d’un point \(P_1\) sur \(\Gamma_1\) on passe via \(A\) à \(P_2\) sur \(\Gamma_2\), puis de \(P_2\) à \(P_3\) sur \(\Gamma_3\) via \(B\), etc., pour revenir de \(\Gamma_8\) à \(\Gamma_1\) en un point \(P_9\) via \(H\). Repartant alors de \(P_9\), on recommence suivant la même procédure une deuxième série \(P_{10}\), \(P_{11}\) etc., mais via cette fois-ci les autres points \(A’\), \(B’\), …, \(H’\), pour terminer par \(P_{17}\) sur \(\Gamma_1\). Les points \(\,P_1\) et \(\,P_{17}\) sont alors les mêmes ; autrement dit, la droite \(\,P_1P_{16}\) passe par \(\,H’\).
Pour le vérifier il suffit de sommer les angles de rotation donnant \(\vec{O_2P_2}\) à partir de \(\vec{O_1P_1}\), puis \(\vec{O_3P_3}\) à partir de \(\vec{O_2P_2}\), etc. Ces angles sont \((\vec{O_1A’},\,\vec{O_2A’})\), puis \((\vec{O_2B’},\,\vec{O_3B’})\), jusqu’à \((\vec{O_8H’},\,\vec{O_1H’})\), suivis de \((\vec{O_1A},\,\vec{O_2A})\), puis \((\vec{O_2B},\,\vec{O_3B})\), etc., et enfin \((\vec{O_8H},\,\vec{O_1H}).\) Comme \(A\) et \(A’\) sont symétriques par rapport à la droite \(O_1O_2\), les angles \((\vec{O_1A’},\,\vec{O_2A’})\) et \((\vec{O_1A},\,\vec{O_2A})\) sont opposés et leur somme est nulle ; il en va de même pour les sept autres paires, d’où finalement \({(\vec{O_1P_1},\,\vec{O_1P_{17}})=0}\), c’est-à-dire \(P_{17}\) = \(P_1\).
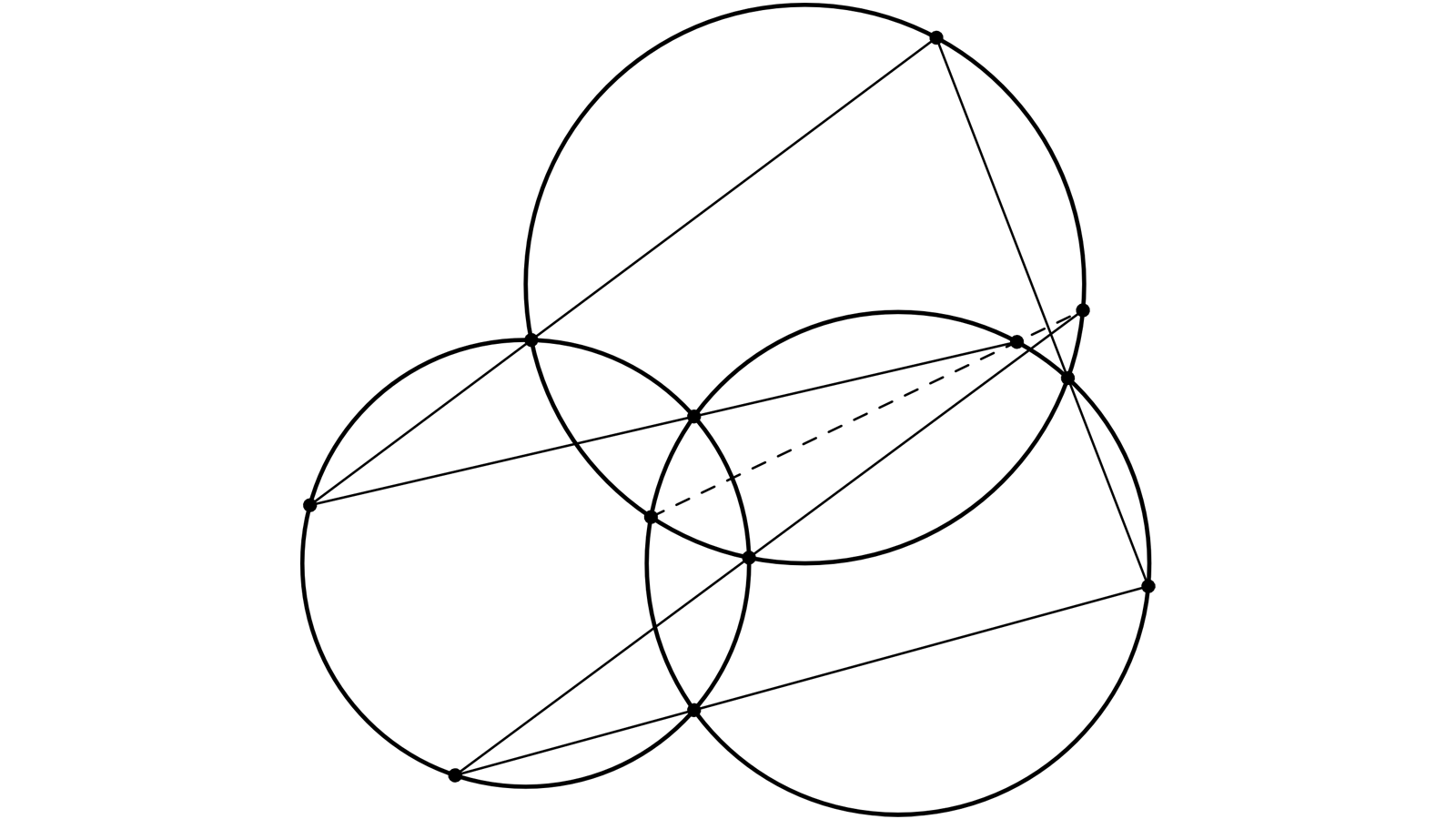
C’est cette situation, dans le cas de trois cercles, qu’illustre la figure proposée par le site, et reproduite (en étiquetant les points) sur la figure 3. L’alignement de \(P_6\), \(C’\) et \(P_1\) dit que \(P_7\) = \(P_1\).
17h45
remarquable !