Est-ce possible ? J’y crois pas !

• Maths et art

Impossible ? non… mais quel cirque tout de même !

Lorsque quelque personne vient à me dire qu’elle est fâchée avec les maths, la physique et n’en fera jamais, je lui réponds qu’elle en fait en permanence, à son insu.

Comment faites-vous pour tenir debout sur un si petit polygone de sustentation ? Essayez de vous pencher et tentez de songer à tout ce que vous mettez en œuvre … pour ne pas tomber. Vous me direz que vous n’y pensez pas . Soit … mais, pensez-y dorénavant !!!

La nature a mis des millénaires afin de réussir à quitter la position de quadrupède pour la position verticale bipède. En notre période sécuritaire il serait bon d’en revenir à marcher à quatre pattes, voire même ramper si nécessaire. La position est plus stable et moins dangereuse pour la santé. Sauf pour la santé mentale probablement.

Bien évidemment tous les mécanismes en place sont assimilés, ou bien intégrés, au titre de réflexes ou sous-programmes. Mais si vous deviez remplacer votre cerveau par un ordinateur avec les sous-programmes adéquats … calculerait-il assez vite ? En cela les gens du cirque m’étonnent et m’interrogent. Ils nous mettent face à des réalités que nous avons peine à croire, lorsque nous sommes trop rationnels et calculateurs. C’est souvent le cas de l’art, de l’artiste … il fait des choses qui nous semblent impossibles ou que nous n’avions pas imaginées. Calcule-t-il comme un mathématicien ou un physicien ? Bien souvent non. Il tombe, se relève, recommence et finit (si c’est un artiste … et qu’il ne démissionne pas) par obtenir des résultats qui nous étonnent. Je ne m’étendrai pas dans ce billet, mais je pense que si nous avons l’esprit scientifique et rationnel cela a de quoi nous interroger.

Pour illustrer je vous propose l’image ci-dessus. Ce sont deux perchistes qui évoluent sur un mât entre trois et quatre mètres. Ce mât n’est pas fixé au sol et ne repose que sur un disque de 30 ou 40 cm de diamètre. Point besoin d’en rajouter. Essayez de mettre le problème en équation. Puis, tentez de le résoudre et le gérer à la vitesse à laquelle ils évoluent. Je ne pense pas qu’ils accepteraient que vous soyez leur metteur en scène … ils auraient trop peur de chuter !

Sur l’image du haut nous avons un monocycliste (Kenzo Tokuoka, un des deux perchistes) . Polygone de sustentation … presque nul. En mouvement, soit … il y a les lois de la dynamique mais lorsqu’il reste sur place et qu’il vous fait ses numéros ?!.

A cette personne j’ai dit qu’il était le « vecteur normal à la surface » et voilà que nous sommes partis tenter d’évoluer sur des surfaces non planes. Premières tentatives ; nous sommes allés sur une piste de skateboard. Enfin lui, car pour moi … je ne suis pas fou ! Sans véritable succès … faut pas croire ! Mais il arrive déjà à évoluer sur quelques plans inclinés. Cela le motive, il n’avait pas songé évoluer sur de telles surfaces. Mission impossible ? Qu’elle pesanteur ! De mon côté cela me fait gamberger sur des systèmes susceptibles de compenser cette pesanteur. Bien sûr il y a la solution de la force centrifuge, et j’ai trouvé dans un livre de physique cette illustration qui relate l’existence d’une structure en forme de paraboloïde de révolution en rotation.

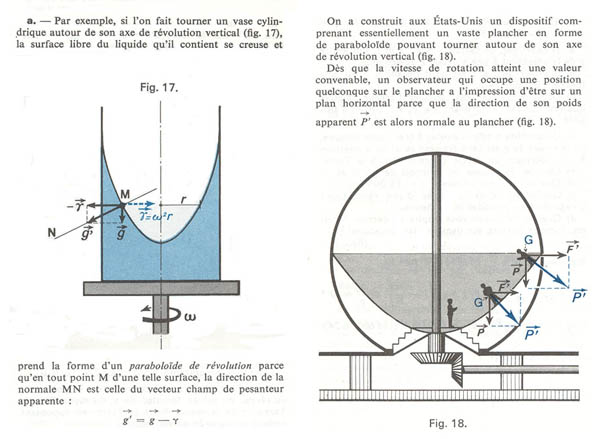
eci me fait songer à la réalisation de Piotr Kowalski, artiste à orientation scientifique, qui proposa une œuvre constituée d’un disque en rotation, sur lequel il avait semé des graines de blé. Imaginez la direction que prenaient les tiges de blé en se développant et la forme de l’ensemble : une allure de cône. Je me souviens, également, d’être resté surpris et étonné par une vidéo à la Cité des Sciences. Elle relatait une expérience de croissance de plantes en apesanteur dans la station orbitale… une figure plutôt échevelée où les racines et les tiges s’emmêlaient… aucune direction ni sens n’étant privilégiés.

Peut-être qu’un voyage sur la lune nous irait bien… la pesanteur y est moins grande. Mais sur terre pas question d’être dans… la lune !

Images extraites du spectacle Carré Curieux par la compagnie du même nom. Photographe : Christophe Raynaud De Lage