Équation de Schrödinger

• Systèmes dynamiques
• Physique

• Ressources pédagogiques

Expérience des fentes de Young

L’expérience des fentes de Young, montrée ici dans sa version quantique, est l’une des plus connues permettant de mettre en évidence les propriétés ondulatoires d’un système physique. La simulation montre un paquet d’onde, représentant une particule quantique, lancée contre une cloison percée de deux fentes. Les couleurs représentent la phase de la fonction d’onde, alors que la luminosité dépend de son module au carré, qui représente la probabilité de détecter la particule. La nature ondulatoire de l’équation de Schrödinger est mise en évidence par l’apparition de franges d’interférence à droite de la cloison percée. Ce sont des bandes dans lesquelles l’intensité alterne entre des valeurs fortes et faibles, qu’il serait difficile d’expliquer dans un modèle classique de la particule. Les conditions aux bords sont périodiques, c’est-à-dire que les bords gauche et droit du rectangle de simulation sont identifiés, de même que les bords supérieur et inférieur. Ceci permet de voir plusieurs passages de la fonction d’onde à travers la cloison, dans le sens gauche-droite ainsi que le sens droite-gauche.

Équation de Schrödinger dans un stade

Simulation de l’équation de Schrödinger dans un domaine en forme de stade (un rectangle auquel on a ajouté deux demi-disques). La couleur représente la phase de la fonction d’onde, alors que l’intensité lumineuse dépend de son module au carré, qui représente la probabilité de détecter une particule quantique à différents endroits. En mécanique classique, le billard dans un stade est un exemple de système dynamique chaotique. Toutefois, ce système admet également des trajectoires non chaotiques : ce sont notamment celles partant à angle droit d’une des parties plates du bord, et font des allers-retours entre les côtés opposés du rectangle. La fonction d’onde, solution de l’équation de Schrödinger, a un comportement moins stable. Toutefois, en la choisissant, comme dans cette simulation, de manière à décrire une particule relativement bien localisée, ayant une vitesse concentrée autour de la verticale (tout en respectant le principe d’incertitude), on obtient une solution qui ne perd sa cohérence que lentement.

Équation de Schrödinger dans une ellipse

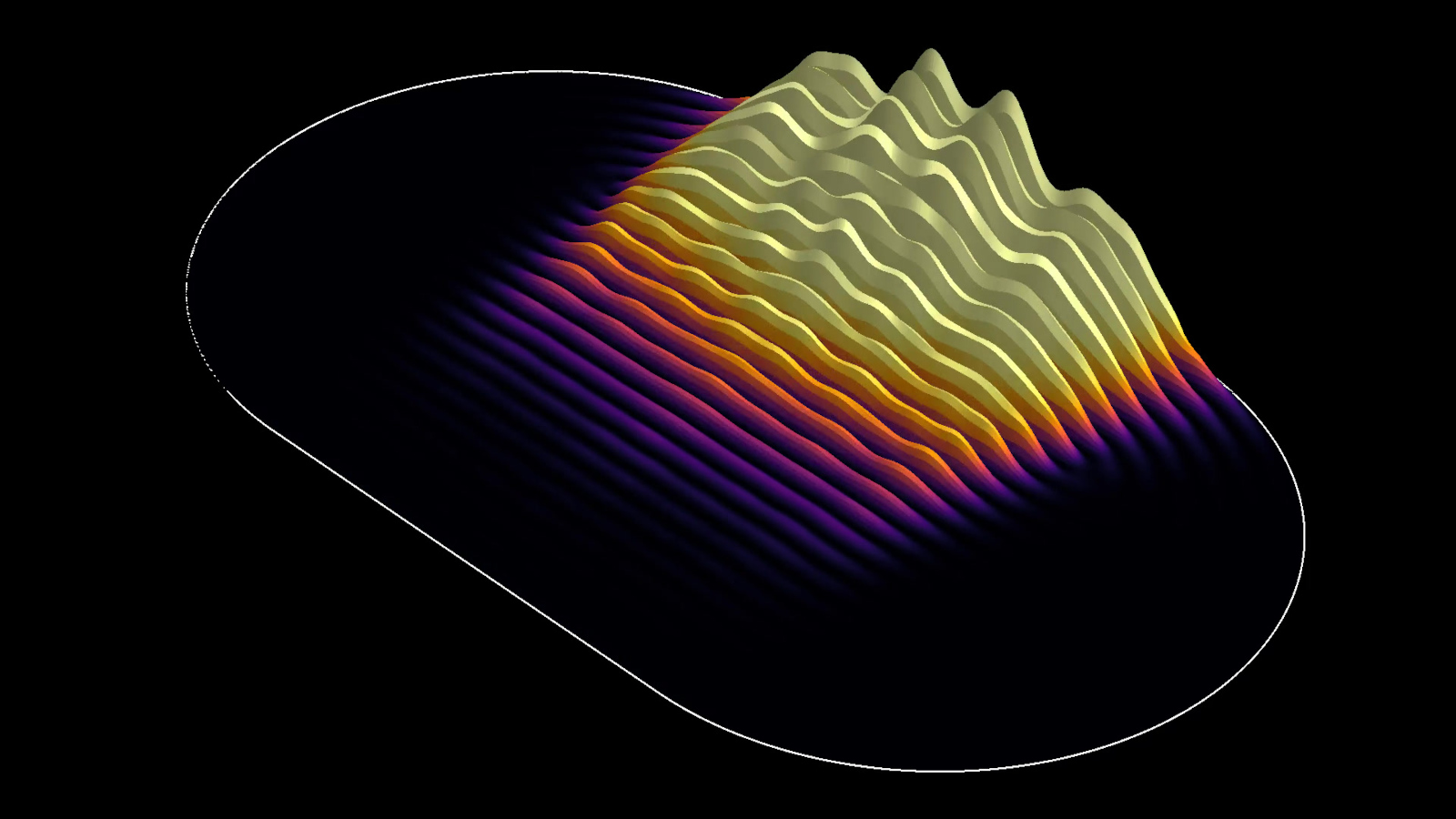
Simulation de l’équation de Schrödinger dans une enceinte en forme d’ellipse. L’état initial est un paquet d’ondes gaussien. C’est un état qui présente un compromis entre l’incertitude sur la position de la particule quantique et celle sur sa vitesse, imposées par le principe d’incertitude de Heisenberg.

La vidéo comporte deux parties, montrant la même simulation avec des palettes de couleur différentes. Dans la première partie, la couleur et la troisième dimension représentent le module de la fonction d’onde au carré, qui donne la probabilité de détecter la particule. Dans la seconde partie, la troisième dimension et la luminosité représentent à nouveau le module au carré, alors que la couleur dépend de la phase de la fonction d’onde. On pourra remarquer le rôle particulier joué par les foyers de l’ellipse.