Il y a quelques temps j’ai assisté à une conférence de Misha Gromov dans laquelle il a en gros commencé de la façon suivante : « Deux plus deux égale quatre. En fait, ce qui est intéressant, c’est plutôt que quatre égale deux plus deux ». Dans ce billet, je voudrais expliquer ce début d’exposé un peu provocateur.
En langage mathématique, l’énoncé que Gromov voulait souligner s’énonce ainsi : « il y a un morphisme
non trivial du groupe des permutations de quatre éléments dans celui des permutations de trois éléments. »
Je vais tenter d’expliquer ce que ça veut dire, et le lien avec \(4=2+2\). Je ne réussirai sans doute pas, en tout cas pas dans ce billet, à expliquer complètement pourquoi c’est intéressant ; sachez toutefois que c’est un phénomène très rare, qui n’arrive pas avec d’autres nombres. C’est à ma connaissance un des exemples les plus simples d’idée mathématique qu’il est possible d’expliquer entièrement à tout le monde,
et cette simplicité en fait la beauté ; j’espère que c’est une motivation suffisante !
De quatre à trois
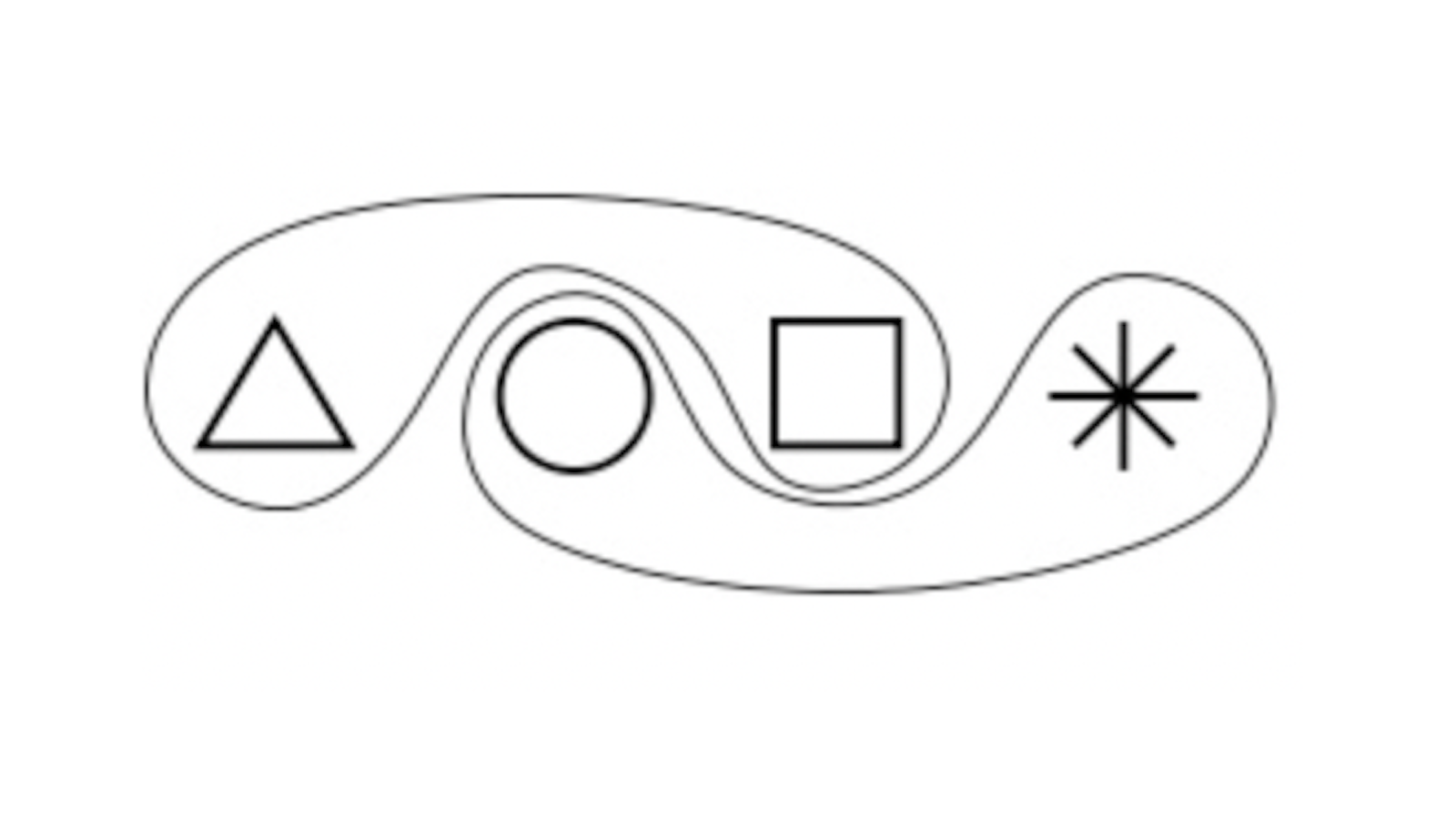
Revenons donc à \(4=2+2\). Cette égalité signifie que si l’on prend \(4\) objets, on peut les séparer en un paquet de \(2\) et un paquet de \(2\). Par exemple :
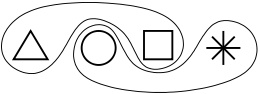
fig1
Comptons combien de façons de faire il existe ; c’est ici que le nombre \(3\) apparaît. En effet, une fois qu’on a choisi par exemple quel objet va accompagner le triangle, on est obligé de constituer le deuxième paquet avec les deux objets restants. Il n’y a donc que \(3\) possibilités : mettre le triangle avec le carré (et donc l’étoile avec le rond), ou avec l’étoile, ou avec le rond.
Permutation
Parlons maintenant de {permutations}. Permuter nos quatre objets, c’est simplement les échanger les uns avec les autres. Par exemple, on peut échanger le triangle avec le rond :
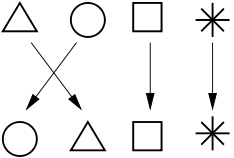
fig2
échanger à la fois le triangle avec le rond et le carré avec l’étoile :
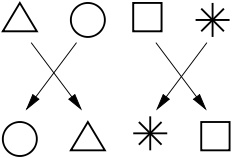
fig3
ou encore envoyer le triangle à la place du rond, le rond à la place du carré, et le carré à la place
du triangle :
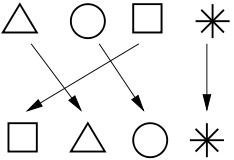
fig4
Il y a bien sûr encore beaucoup de façon de procéder (combien en tout à votre avis ?). On peut composer des permutations, c’est-à-dire les effectuer l’une après l’autre, et le résultat est encore une permutation ; il y a une permutation où chaque objet reste à sa place initiale (on l’appelle l’identité) et enfin toutes les permutations sont inversibles : on peut trouver une nouvelle
permutation qui défait ce qu’a fait la première, c’est-à-dire ramène chaque objet à sa place initiale.
Ces propriétés font qu’on parle du {groupe} des permutations ; la notion de groupe est fondamentale
dans presque toutes les branches des mathématiques. Par exemple, en géométrie, l’ensemble des symétries
d’une figure forme un groupe.
Un petite remarque : quand on compose deux permutations, l’ordre est important (on dit que le groupe des permutations est non commutatif). Ça ne doit pas vous étonner, car beaucoup d’opérations de la vie courante sont non commutatives ; par exemple mettre ses chaussures puis ses chaussettes ne donne pas le résultat en général escompté.
Le « morphisme »
Considérons une permutation fixée, quelconque de nos quatre objets, que nous appellerons \(\sigma\) (sigma). Par exemple, prenons la dernière que nous avons dessinée ci-dessus : elle envoie le triangle à la place du rond, le rond à la place du carré, et le carré à la place du triangle et laisse l’étoile à sa place.
Ce que permet d’affirmer la discussion autour de \(4=2+2\), c’est qu’on peut fabriquer avec cette permutation une nouvelle permutation qui, elle, {agit} sur {{trois}} objets (c’est à dire échange ces trois objets les uns avec les autres). Les objets en question ne sont plus les symboles rond, carré, triangle, étoile,
mais les trois séparations possibles de ces symboles.
En effet, si on prend une séparation des quatre objets initiaux en deux paquets, en échangeant les objets suivant notre permutation on obtient une nouvelle séparation en deux paquets de \(2\) :
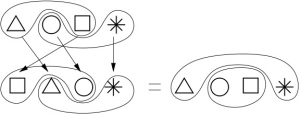
On dit que \(\sigma\) {induit} une permutation sur les trois séparations. Évidemment, si on compose deux permutations \(\sigma\) et \(\sigma’\) des quatre objets initiaux et qu’on regarde ce qui se passe sur les
trois séparations possibles, on obtient la composée des permutations induites : en mathématique on parle
alors de {morphisme}. Le morphisme est ici le procédé de fabrication d’une permutation de trois éléments à partir d’une permutation de quatre éléments.
Voici la description complète de la permutation sur les séparations qu’on obtient dans le cas considéré :
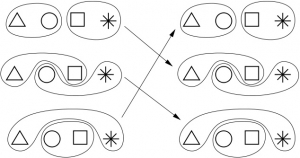
Pourquoi 4 ?
Ce phénomène est très particulier ; en effet, si on essaye la même chose avec \(6\) au lieu de \(4\), on va chercher le nombre de séparations de six objets en deux paquets : il y en a \(10\). Et comme \(10\) est plus grand que \(6\), ce n’est pas très intéressant : il est en effet facile de fabriquer une permutation de \(10\) objets à partir d’une permutation de \(6\) objets : il suffit d’ajouter \(4\) objets qui ne bougent jamais au \(6\) initiaux. On peut essayer avec d’autres valeurs, mais \(4=2+2\) est une formule « exceptionnelle », dans le sens où le morphisme construit n’a pas d’analogue.
Dans un prochain billet, j’essayerai d’expliquer le rôle des permutations dans la géométrie ; on verra réapparaître de objets qui vont par quatre ou par trois, et on pourra illustrer notre morphisme grâce… à un simple cube.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.