Deux ou trois choses que je sais d’Émile Picard…

Grand pouvoir et grands théorèmes

• Monde de la recherche

Il y a quelques mois, au cours d’un exposé donné devant, entre autres, de nombreux apprenti⋅e⋅s mathématicien⋅ne⋅s ¹Il y avait un public assez varié, les « jeunes » étaient des élèves de l’École normale supérieure de Lyon (ENS), j’ai évoqué le pouvoir dont disposaient, pendant la première moitié du vingtième siècle, certains membres de l’Académie des sciences ² Le logo de ce billet est une photographie de la coupole de l’Institut, à Paris, sous laquelle se tiennent notamment les cérémonies de l’Académie des sciences.. Il paraît que certains de ces jeunes ignoraient qu’il pût être question de pouvoir dans le monde pur des mathématiques.

Une parenthèse : du pouvoir...

Il y a pourtant, aujourd’hui encore, des postes de pouvoir, et nos jeunes y sont confrontés. Pour les « ignorants » (que l’on ne voie rien de péjoratif dans ce mot, qu’on le prenne comme synonyme d’« innocents »), en voici quelques exemples :

• diriger une revue scientifique donne le pouvoir d’accepter ou de refuser de publier des articles
• diriger un laboratoire (une UMR ³Unité mixte de recherche, le laboratoire dans lequel travaillent la plupart des mathématiciens français, le mot « mixte » signifie que cette entité est soutenue par le CNRS et une université.) donne le pouvoir de répartir les subsides disponibles entre les membres de cette UMR
• présider une commission de spécialistes (ceci n’existe plus, j’y reviens plus bas) donne un pouvoir certain sur le choix des mathématiciens recrutés ; de même, être membre de la « commission » du CNRS qui recrute les nouveaux chercheurs,
• être membre du CNU donne un pouvoir sur les promotions des collègues.

Il y a bien d’autres postes de pouvoir (une commission qui attribue des primes aux enseignants-chercheurs, le ministère, la direction scientifique du CNRS, les nouveaux « comités de sélection » ⁴qui remplacent les commissions de spécialistes…) mais ils fonctionnent d’une manière que je connais moins bien (sans doute parce qu’elle est moins transparente et moins collégiale), je ne peux donc les évoquer dans ce « billet » qui, par définition, est un article court.

La liste des postes de pouvoir dressée ci-dessus se compose de postes dont les détenteurs sont connus du « public », qui sont tous plus ou moins collégiaux et dont les règles de fonctionnement sont, elles aussi, publiques — une garantie pour les « administrés ». De plus, presque toujours, ces postes sont tenus par des mathématiciens en pleine activité scientifique, et tournent — ce qui ne veut pas dire qu’il n’y a jamais d’erreurs, ni d’abus ⁵Bien des pouvoirs plus « occultes » sont détenus par ce que l’on pourrait appeler des « technocrato-universitaires », parfois coupés du monde de la recherche et qui n’en prennent pas moins des décisions..

Le tout-puissant Émile Picard

Il en allait tout autrement pendant la période que j’évoquais dans l’exposé dont il était question au tout début de ce billet ⁶Qui portait sur les publications, notamment aux Comptes rendus de l’Académie des sciences, pendant la période de Vichy. Une version préliminaire d’un article à paraître dans la Revue d’histoire des mathématiques sur ce sujet est disponible ici.. Le cas d’Émile Picard ⁷J’ai évoqué très brièvement celui de Cauchy dans un billet précédent. Nous nous rapprochons du temps présent. est impressionnant :

• secrétaire perpétuel de l’Académie des sciences de 1917 à sa mort en 1941 et s’occupant donc de la publication des Comptes rendus de l’Académie des sciences, dirigeant ou participant aux comités de rédaction du Journal de mathématiques pures et appliquées, du Bulletin des sciences mathématiques et des Annales scientifiques de l’École normale supérieure, il contrôlait ainsi toutes les publications mathématiques en France, sauf le Bulletin de la Société mathématique de France,
• comme secrétaire perpétuel encore, il avait un immense pouvoir sur les élections de membres de l’Académie des sciences, mais aussi son mot à dire sur les élections de professeurs au Collège de France ou d’astronomes à l’Observatoire,
• il pesait de tout son poids sur les élections de professeurs à la Sorbonne,
• comme président du Conseil international des recherches, il a pu imposer ses opinions anti-allemandes et organiser le boycott des scientifiques allemands après la première guerre mondiale.

Bien entendu, les pouvoirs s’accumulent, et tout ceci lui donnait toute une cour de collègues qui lui étaient redevables… et lui permettaient d’exercer sa puissance par leur intermédiaire ⁸Picard cumulait aussi les postes d’enseignement. Ce sont quarante-six promotions de normaliens qui ont suivi ses cours, sans compter les sévriennes, qui, plus délurées qu’on ne l’imagine parfois, l’avaient surnommé Roméo, et les centraliens — une influence scientifique considérable..

Il ne faut pas croire (je m’adresse toujours aux « innocents ») que, parce que Picard était un grand scientifique — les théorèmes auxquels il a laissé son nom sont des joyaux de l’analyse complexe (voir ci-dessous), quant au groupe de Picard et aux extensions de Picard-Vessiot, ce sont aussi des bijoux rutilants dont nous ne saurions nous passer — cette concentration de pouvoir entre ses seules mains n’ait pas entraîné des injustices, voire des situations scandaleuses. Je donnerai ici deux exemples

• celui d’un mathématicien profond et novateur, Pierre Fatou ⁹Le nom de Pierre Fatou apparaît dans plusieurs articles déjà publiés sur ce site, par exemple celui-ci., dont la lenteur et la modestie de la carrière (il a été, presque toute sa vie, astronome-adjoint à l’Observatoire) doivent beaucoup à Picard,
• l’inimaginable boycott par l’Académie des sciences d’Albert Einstein venu donner une série de conférences à Paris en 1922 (à l’invitation de Paul Langevin). De façon moins ponctuelle, le boycott des mathématiciens allemands dans les années 1920 a entraîné un isolement très préjudiciable, au moment où des mathématiciens allemands inventaient, entre autres, l’algèbre moderne (Emmy Noether) et la topologie générale (Felix Hausdorff).

Bref. Une des raisons les plus banales de s’intéresser à l’histoire est d’en tirer des leçons pour aujourd’hui ¹⁰Je regrette de me répéter.. Disons que… Concentrer les pouvoirs nuit gravement à la santé des mathématiques.

Un « petit » théorème de Picard

Je ne résiste pas au plaisir d’énoncer un des théorèmes de Picard… quelques lignes techniques en fin de billet, avec une image en note pour me faire pardonner. Ce théorème, dit « petit » théorème de Picard ¹¹Il y a beaucoup de théorèmes de Picard, un autre a un énoncé presque analogue à celui du « petit » et est appelé « grand théorème de Picard »… affirme la chose suivante : Une fonction entière non constante prend toutes les valeurs sauf peut-être une.

Ce qu’on appelle une fonction entière, c’est une fonction qui associe à tout nombre complexe un nombre complexe et qui est holomorphe, c’est-à-dire dérivable. Par exemple, la fonction exponentielle complexe ¹² Il y a quelques années, écrivant un article pour un magazine de popularisation scientifique (je ne dirai pas lequel des deux), j’avais préparé un « encadré » pour expliquer ce qu’était la fonction exponentielle.

Les lecteurs de nom-du-journal savent ce qu’est la fonction exponentielle,
me fut-il objecté, et il n’y eut pas d’explication dans l’article.

A Images des mathématiques, nous avons une autre conception de la popularisation… Voici donc une image de la fonction exponentielle, copiée ici.
La partie colorée, sorte d’escalier en colimaçon, est l’ensemble des nombres complexes, représentée de façon que l’exponentielle soit la projection verticale, le parallélogramme horizontal en bas représente aussi les nombres complexes, espace d’arrivée. Chaque point du parallélogramme est l’image de tous les points à la verticale… sauf que le centre, \(0\), n’est l’image de personne.


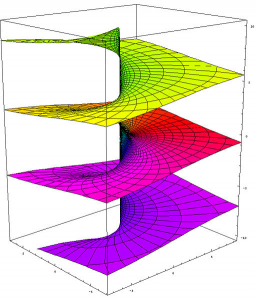
associe à tout nombre complexe un nombre complexe non nul et tous les nombres complexes non nuls sont atteints (une infinité de fois) : elle évite de prendre la valeur 0 mais prend toutes les autres. Eh bien, le théorème de Picard affirme que c’est le cas en général : les fonctions de variable complexe ont tendance à être presque surjectives !