
Les ateliers MATh.en.JEANS sont des activités proposées à des collégiens ou lycéens encadrées par un professeur et un chercheur. Les jeunes réfléchissent sur un sujet proposé par le chercheur.
Le but est de faire découvrir les mathématiques sous une forme ludique et créative qui sort du cadre scolaire.
J’ai le plaisir d’accompagner (Il faut bien dire que c’est le professeur, Véronique Dupuits, qui assure la plus grosse part du travail) deux groupes qui viennent du collège Saint-Dominique de Nancy.
Ce qui m’a le plus étonné, c’est la manière dont les jeunes se sont mis à penser comme des mathématiciennes et mathématiciens. Sans qu’on leur ait particulièrement donné ces consignes, certains formulaient des hypothèses —parfois fausses parfois parfaitement justes —, avançaient des arguments que d’autres réfutaient ou avec lesquels ils tombaient d’accord. Ainsi, ils avançaient en utilisant les personnalités. Certains sont plus imaginatifs, d’autres plus rigoureux pour la démonstration et d’autres encore plus doués pour faire des dessins.
Je crois que l’objectif est vraiment atteint quand on sort de la relation enseignant-élève et que les élèves eux-mêmes prennent le raisonnement en main.
Pour vous faire partager un peu leurs recherches, voici les deux questions auxquelles ils ont été confrontés.
Polygones équidécomposables
Aux cinquièmes, une question de géométrie plane a été posée. Etant donnés deux polygones, puis-je découper le premier avec une paire de ciseaux, déplacer les morceaux et reconstituer le second polygone ?
Bien sûr, la première remarque est que ces deux polygones doivent avoir même aire. Est-ce la seule condition ? Peut-on écrire un algorithme qui répond au problème ?
-

Explication du passage d’un triangle à un rectangle de même aire.
-
Décomposition d’un polygone quelconque en triangles.
Polyèdres réguliers
Les quatrièmes ont gagné une dimension et se sont intéressés aux polyèdres réguliers. Un polyèdre (convexe) est un objet en trois dimensions avec des faces planes sans creux. Un polyèdre est régulier si toutes ses faces sont des polygones réguliers (tous les côtés ont même longueur) avec un même nombre de côtés et tous les sommets sont entourés d’un même nombre de faces.
Par exemple, un cube est un polyèdre régulier. Toutes les faces sont des carrés et autour de chaque sommet, il y a trois cubes. Quels sont tous les polyèdres réguliers ?
-

Réalisation d’un icosaèdre en papier.
-
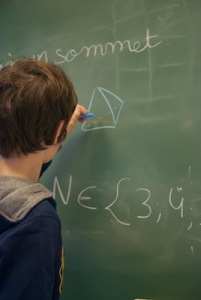
Vue en perspective du tétraèdre.
-

Preuve que le nombre de côtés d’une face est limité.
-

Avec des faces hexagonales, on ne peut construire de polyèdres. On reste dans un plan.
Maintenant, le congrès MATh.en.JEANS approche et toute l’énergie est consacrée à la préparation de celui-ci. Pour nous, ce sera à l’université de Valenciennes et du Hainaut-Cambrésis, où nous retrouverons environ 500 autres personnes. Les jeunes présenteront leurs recherches et animeront des stands autour du sujet de leur atelier.
Je suis impatient de voir comment cela va se passer pour nos deux ateliers nancéens.
-

.



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.