
Premier défi : le problème du mois
Placer les nombres de \(1\) à \(8\) sur les faces d’un octaèdre de telle sorte que la somme des faces ayant un sommet en commun soit toujours la même.


Solution du premier défi
Étant donné un sommet \(S\), on appellera « pyramide de sommet \(S\) » l’ensemble des quatre faces autour de \(S\).
Comme la somme des nombres de \(1\) à \(8\) est égale à \(36\), en faisant la somme sur deux pyramides opposées, on voit que la somme des faces de chaque pyramide est nécessairement égale à \(18\).
Considérons maintenant la face marquée \(1\) et une de ses faces voisines. Ces deux faces font partie d’exactement deux pyramides. Il doit donc exister deux paires \(\{b,c\}\) et \(\{b’,c’\}\) telles que \(18=1+a+b+c=1+a+b’+c’\) et où \(1\), \(a\), \(b\), \(b’\), \(c\) et \(c’\) sont deux à deux distincts.
En prenant \(a=2\), par exemple, on doit avoir \(b+c=b’+c’=18-1-2=15\), ce qui nous donne une seule solution : \(7+8\). Deux telles paires n’existent donc pas pour \(a=2\).
En faisant une analyse similaire, on voit que \(a\) ne peut prendre que les valeurs \(a=4,6,7\) ou \(8\). Prenons par exemple \(a=6\) : on obtient \(b+c=b’+c’=18-1-6=11\) et donc les paires \(\{4,7\}\) et \(\{3,8\}\) conviennent.
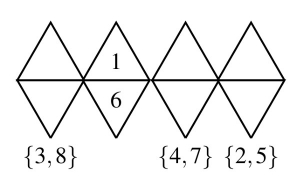
On va donc maintenant essayer de remplir le patron suivant en mettant les paires \(\{4,7\}\) et \(\{3,8\}\) dans les parallélogrammes adjacents au parallélogramme \(\{1,6\}\). La paire \(\{2,5\}\) sera donc dans le dernier parallélogramme.
.
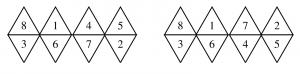
Comme on a vu que \(1\) et \(3\) ne peuvent pas être voisins, on a nécessairement \(8\) sur le triangle du haut et \(3\) sur le triangle du bas. Enfin, comme la somme des quatre triangles du haut doit être égale à \(18\), on obtient alors les deux solutions ci-dessous.
.
En raisonnant de manière analogue avec une autre valeur possible de \(a\), on peut obtenir d’autres solutions.
Deuxième défi
Quel est le carré de taille minimale que l’on peut recouvrir avec des pièces de la forme suivante?
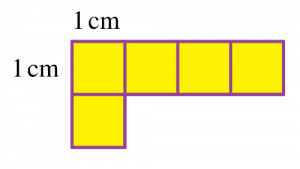


Solution du deuxième défi
La pièce faisant \(5\,{\rm cm}^2\), le côté du carré recouvert est nécessairement un multiple de \(5\,{\rm cm}\). Par quelques essais, on peut voir que l’on ne peut pas recouvrir un carré \(5\,{\rm cm}\,\times\, 5\,{\rm cm}\). Par contre, il est possible de recouvrir un carré \(10\,{\rm cm}\,\times\, 10\,{\rm cm}\)

Troisième défi
Par quel jour doit commencer une année non bissextile pour qu’il y ait exactement cinq mois contenant cinq dimanches chacun ?


Solution du troisième défi
La réponse est : le dimanche. Dans une année non bissextile, on compte un mois de \(28\) jours qui contiendra toujours exactement quatre dimanches, sept mois de \(31\) jours et quatre mois de \(30\) jours. Le reste de la division euclidienne de \(30\) par \(7\) est \(2\) et celui de \(31\) par \(7\) est \(3\). Ainsi, un mois de \(30\) jours contiendra cinq dimanches si son premier jour est samedi ou dimanche, tandis qu’un mois de \(31\) jours contiendra cinq dimanches si son premier jour est vendredi, samedi ou dimanche. Si, par exemple, le \(1^{\text{er}}\) janvier tombe un dimanche, alors le \(1^{\text{er}}\) février sera un mercredi, le \(1^{\text{er}}\) mars sera un mercredi, le \(1^{\text{er}}\) avril sera un samedi, le \(1^{\text{er}}\) mai un lundi, le \(1^{\text{er}}\) juin un jeudi, le \(1^{\text{er}}\) juillet un samedi, le \(1^{\text{er}}\) août un mardi, le \(1^{\text{er}}\) septembre un vendredi, le \(1^{\text{er}}\) octobre un dimanche, le \(1^{\text{er}}\) novembre un mercredi et le \(1^{\text{er}}\) décembre un vendredi. On obtient ainsi cinq mois (janvier, avril, juillet, octobre, décembre) contenant exactement cinq dimanches. En refaisant le même raisonnement en changeant le jour de départ, on s’aperçoit que si le \(1^{\text{er}}\) janvier n’est pas un dimanche alors il n’y a que quatre mois contenant cinq dimanches.
Quatrième défi
Jules commande quatre paires de chaussettes vertes et quelques paires rouges. Le prix unitaire des chaussettes vertes est deux fois plus élevé que le prix des rouges. Le vendeur se trompe dans la commande et échange les nombres de paires rouges et vertes. Le prix final est \(50\,\%\) plus élevé que celui attendu par Jules. Combien de paires rouges Jules avait-il commandées ?


Solution du quatrième défi
La réponse est : \(16\) paires. Notons \(r\) le nombre de paires rouges commandées par Jules et \(p\) le prix d’une paire rouge. Le prix des paires vertes étant \(2p\), le prix attendu par Jules est donc \(r\times p+4\times 2p=(r+8)p\).
Le prix facturé est donc \(1{,}5(r+8)p\). Comme le vendeur a échangé le nombre de paires de chaque couleur, le prix facturé est aussi égal à \(4p+r\times 2p=(4+2r)p\). On obtient alors \[\frac32 (r+8)p=(4+2r)p.\] Cela donne \(r=16\).
Cinquième défi
Une calculatrice affiche les nombres à l’aide de segments horizontaux et verticaux. Par exemple, le nombre \(319 \;\) utilise \(13\;\) segments.

Combien de nombres à deux chiffres peut-on écrire avec exactement \(12\;\) segments ?


Solution du cinquième défi
La réponse est : \(12\) nombres possibles. On compte tout d’abord combien chaque chiffre utilise de segments. Le chiffre \(1\) utilise deux segments; \(2\), \(3\) et \(5\) en utilisent cinq ; \(4\) en utilise quatre ; \(0\), \(6\) et \(9\) en utilisent six ; \(7\) en utilise trois et enfin \(8\) en utilise sept. Le nombre \(12=5+7=6+6\) s’écrit de deux façons comme somme de deux entiers dans l’ensemble \(\{2,3,4,5,\) \(6,7\}\). On obtient \(3\times 2=6\) nombres pour la décomposition \(5+7\) qui sont \(28\), \(82\), \(38\), \(83\), \(58\) et \(85\). On obtient \(3\times 3-3=6\) nombres pour la décomposition \(6+6\) (les nombres \(00\), \(09\) ou \(06\) ne sont pas considérés comme des nombres à deux chiffres) qui sont \(60\), \(90\), \(66\), \(69\), \(96\) et \(99\). En tout, on a \(12\) nombres possibles.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock


17h31
Soit \(S\) la somme magique. Comme les faces sont triangulaires, si on additionne les sommes obtenues sur les \(6\) sommets, chaque nombre de \(1\) à \(8\) sera compté \(3\) fois. Donc \(6S = 3(1+2+3+4+5+6+7+8)\), d’où \(S=18\).
Pour chacun des \(3\) sommets de la face \(8\), les \(3\) autres faces doivent former une partition de \(18-8=10\) en \(3\) nombres distincts. De plus les \(3\) faces voisines de la face \(8\) ont chacune \(2\) sommets communs avec elle, donc elles portent des nombres apparaissant dans \(2\) des \(3\) partitions de \(10\). Il y a en fait \(4\) partitions de \(10\) en \(3\) nombres distincts : \(10 = 7+2+1 = 6+3+1 = 5 + 4 + 1 = 5 + 3 + 2\). Seuls les nombres \(1,2,3,5\) apparaissent dans \(2\) partitions. Il faut donc choisir \(3\) nombres \(a,b,c\) parmi eux et les placer autour de \(8\). On en déduit alors les nombres des faces opposées : \(10-b-c,10-a-c, 10-a-b\), puis la face opposée à \(8\) : \( 18 -a -(10-a-b)-(10-a-c) = a+b+c-2 \). Mais il ne faut pas que \(a+b+c=10\), sinon ils apparaîtraient sur \(2\) faces chacun, ce qui exclut la combinaison \(2,3,5\). Il reste donc les \(3\) autres combinaisons , et on peut vérifier qu’elles donnent toutes une solution, que j’ai représentées sous la forme
\( \frac{pyramide du haut}{pyramide du bas} = \frac{\frac{8, a}{b, 10-a-b}}{\frac{c, 10-a-c}{10-b-c, a+b+c-2}}\)
\( \frac{\frac{8, 1}{2, 7}}{\frac{3, 6}{5, 4}}\)
\( \frac{\frac{8, 1}{2, 7}}{\frac{5, 4}{3, 6}}\)
\( \frac{\frac{8, 1}{3, 6}}{\frac{5, 4}{2, 7}}\)
17h56
Pas mieux, alors on va orienter l’octaèdre avec une pointe en haut et une en bas. On tourne autour de la pyramide du haut en partant de \(8\), puis dans le même sens autour de celle du bas, en partant de la face \(c\), sous le \(8\), toujours vue d’en haut.
\(8,a,10-a-b,b,c,10-a-c,a+b+c-2,10-b-c\)
\(8,1,7,2,3,6,4,5\)
\(8,1,7,2,5,4,6,3\)
\(8,1,6,3,5,4,7,2\)
0h57
Si on appelle S,A,B,C,D et T les sommets de l’octaèdre, pas forcément régulier comme sur ma figure (ce qui n’a aucune
importance ici).
Chaque sommet a en commun 4 faces.
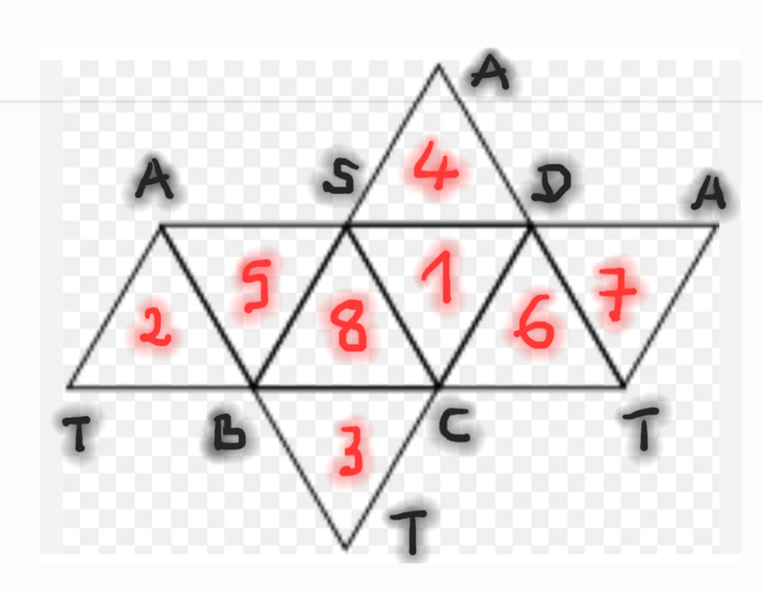
La somme des entiers de 1à 8 vaut n(n+1)/2 avec n=8, donc 36, si on considère 2 sommets opposés comme S et T par exemple,
alors les 8 faces sont utilisées : SAB, SBC, SCD, SDA d’une part et
TAB, TBC, TCD,TDA d’autre part, donc la somme des faces utilisant S ( ou T) vaut 36/2 soit 18.
Il y a 8 manières d’obtenir 18 en utilisant 4 des entiers de 1à 8: 18=8+/+2+1=8+6+3+1=8+5+4+1=8+5+3+2=7+6+4+1=7+6+3+2=
7+5+4+2=6+5+4+3
En présentant les résultats sur un « patron deplié » de l’octaèdre, on aura par exemple
9h09
2ème défi
L’aire d’une pièce est \(5\) donc l’aire du carré est multiple de \(5\). C’est donc un carré de côté \(5n\). Il y a une solution simple pour \(n=2\) : avec \(2\) pièces on forme un rectangle \(2\) x \(5\), et avec \(10\) rectangles il est facile de paver le carré \(10\) x \(10\).
Essayons avec \(n=1\). On colorie les cases du grand carré alternativement en noir et blanc comme un échiquier. Si on commence par exemple avec un coin noir, alors on aura \(13\) cases noires, dont les \(4\) coins, et \(12\) blanches. Comme la plus grande dimension d’une pièce est \(4\), aucune ne peut couvrir \(2\) coins donc il faut \(4\) pièces distinctes pour couvrir les \(4\) coins. Or toute pièce placée dans un coin couvre \(2\) cases noires et \(3\) blanches, donc les \(4\) pièces des coins couvrent en tout \(8\) cases noires et \(12\) blanches. Il reste alors \(5\) cases noires à couvrir avec une pièce, ce qui est impossible.
Le carré \(10\) x \(10\) est la solution optimale.
18h18
Mon raisonnement pour écarter le carré \(5\)x\(5\) ne tient pas car j’affirme péremptoirement que « toute pièce placée dans un coin couvre \(2\) cases noires et \(3\) blanches », alors que c’est faux, par exemple sur ma solution \(10\)x\(10\) !
Voilà un autre argument pour exclure le carré \(5\)x\(5\).
Disons qu’une pièce est horizontale ou verticale selon qu’elle occupe \(4\) cases d’une même ligne ou d’une même colonne, et soit \(h\) le nombre de pièces horizontales. On colorie en noir les \(h\) lignes dont elles couvrent \(4\) cases chacune, et en blanc les \(5-h\) autres lignes.
Si \(h=5\), alors il y aura une case non couverte dans chaque ligne.
Si \(h=4\), alors après avoir posé les pièces horizontales, il y aura au moins une case non couverte dans chaque ligne, mais l’unique pièce verticale ne pourra en couvrir que \(4\) au mieux.
Si \(h=3\), chaque pièce horizontale couvre au mieux une case blanche, et chaque pièce verticale en couvre \(3\) au mieux, donc au total, sur \((5-2)*5 = 10\) cases blanches, on ne peut pas en couvrir plus de \(3*1 + (5-3)*3 = 9\).
Si \(h < 3\), en tournant le carré d'un quart de tour (avant de colorier), on se ramène à l'un des cas précédents.
Cette fois ça marche mais c'est un peu long. Quelqu'un a-t-il un argument plus élégant ?
13h04
À rotation/symétrie près, il n’y a que 2 positions pour la pièce couvrant le centre. Dans les 2 cas, l’un des coins ne peut alors être couvert que d’une seule manière, qui fait instantanément apparaître un trou non recouvrable.
13h40
Chaque mois compte entre \(28\) et \(31\) jours, soit exactement \(4\) semaines complètes dans tous les cas, et donc \(4\) ou \(5\) dimanches. Avec exactement \(5\) mois comptant \(5\) dimanches, il nous faut donc en tout \(7*4+5*5 = 53\) dimanches. Or une année non bissextile comprend \(365\) jours, et comme \(365 = 1+52*7\), elle contient exactement \(52\) semaines complètes et autant de dimanches du \(2\) janvier au \(31\) décembre inclus. Le premier janvier doit donc être un dimanche.
8h40
4ème défi
Soit \(r\) le nombre de paires rouges et \(p\) le prix unitaire d’une paire rouge. Alors le prix initial est \(4*2p + rp = (8+r)p\), et le prix final est \( 2rp + 4p = (2r+4)p \). Donc le prix a été multiplié par \( (2r+4)p / (8+r)p = (100 +50)/100 = 3/2 \), d’où \(4r + 8 = 24 + 3r\) et donc \(r = 16\).
11h49
Le nombre maximal de segments est \(7\).
Le nombre minimal de segments est donc \(12-7=5\).
On a donc droit aux chiffres à \(6\) et \(6\) segments ensemble: \(90\), \(60\), \(69\), \(96\), \(66\), et \(99\), et aux chiffres à \(5\) et \(7\) segments ensemble deux fois pour chaque couple et il y a trois couples.
\(12\) nombres à deux chiffres ont exactement \(12\) segments.