Défis de février 2024

Écrit par Romain Joly

Publié le 28 février 2024

Premier défi : le problème du mois

Le problème du mois (tous les premiers vendredis du mois, retrouvez « Le défi du mois » : un défi sans mathématique très complexe mais parfois éloigné du cadre scolaire. Il pourrait vous donner du fil à retordre…) :

Combien y a-t-il de façons de placer tous les chiffres de $1$ à $6$ dans les cercles de sorte que la somme des chiffres sur chaque côté soit égale ?

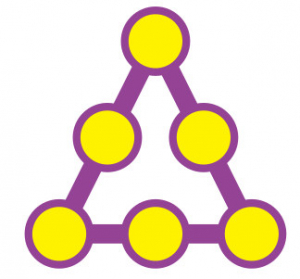
Défi

Solution du premier défi

Réponse : 4 solutions possibles.

Notons $a$, $b$ et $c$ les chiffres situés aux sommets du triangle et $d$, $e$ et $f$ ceux au milieu des côtés. Si $x$ est la somme des chiffres de chaque côté, alors $3x=2(a+b+c)+d+e+f$. Comme $a+b+c+d+e+f= 1+2+\dots +6=21$, on a $3x=(a+b+c)+21$. La somme $a+b+c$ est donc divisible par $3$. Or \[6=1+2+3\leq a+b+c\leq 4+5+6=15.\]
Les possibilités pour $a+b+c$ sont donc $6$, $9$, $12$ ou $15$. Analysons chaque cas:

– si $a+b+c=6$, alors de l’égalité $3x=(a+b+c)+21$, on déduit $x=9$ et l’unique possibilité est alors:

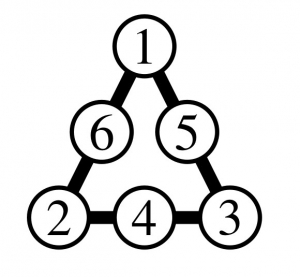
solution 1

– si $a+b+c=9$, alors $x=10$. Le triplet $(a,b,c)$ peut dans ce cas être choisi de trois manières distinctes: $(6,2,1)$, $(5,3,1)$ ou $(4,3,2)$. Pour le premier, il n’y a pas de solution puisque, comme $x=10$, le côté avec $6$ et $2$ devrait contenir un autre $2$ en son milieu, ce qui est interdit par l’énoncé. De même, l’option $(4, 3, 2)$ ne donne aucune solution. Seule l’option $(5,3,1)$ donne l’unique solution suivante :

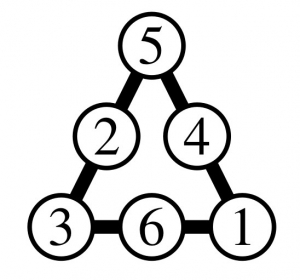
solution 2

– si $a+b+c=12$, alors $x=11$. On a à nouveau trois possibilités pour $(a,b,c)$: $(6,5,1)$, $(6,4,2)$ ou $(5,4,3)$. Seule la seconde donne une solution :

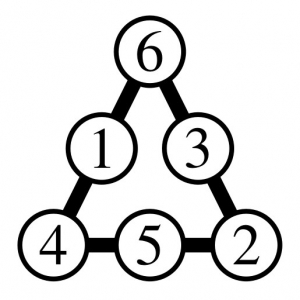
solution 3

– enfin, si $a+b+c=15$, alors $x=12$. L’unique possibilité pour $(a,b,c)$ est $(6,5,4)$, qui nous donne la solution :

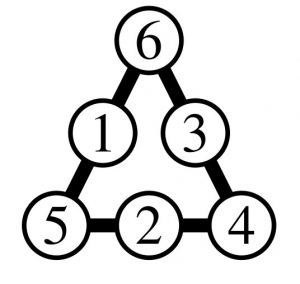
solution 4

Il y a donc (à rotation ou réflexion du triangle près) quatre façons de placer les chiffres dans les cercles.

Deuxième défi

Un nombre à quatre chiffres, tous distincts de $0$, possède la propriété suivante : si l’on supprime les deux chiffres de gauche, le nombre restant est cinq fois plus grand que le nombre formé en supprimant les deux chiffres de droite. Si son chiffre des dizaines est $6$, quel est le nombre original ?

Solution du deuxième défi

Réponse : $1365$

Notons $ab6c$ le nombre à quatre chiffres de départ.

On sait que $6c$ vaut cinq fois le nombre de centaines du nombre original.

On en déduit que $6c$ est un multiple de $5$.

Comme $c\neq 0$, nécessairement $c=5$.

Comme $65=5\times 13$, on en déduit que le nombre cherché est $1365$.

Troisième défi

Dessiner une figure qui a la même aire que la première et le même périmètre que la seconde.

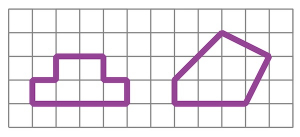
Figures

Solution du troisième défi

Voici une possibilité :

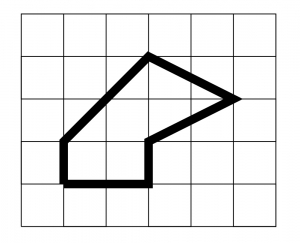
Solution

Quatrième défi

Si la somme de trois entiers positifs consécutifs est égal au produit de ces trois nombres, combien vaut la somme des carrés des trois nombres?

Solution du quatrième défi

Réponse : 14

Notons $n-1$, $n$ et $n+1$ les trois entiers positifs conséecutifs. Par hypothèse, on a :

\[
\begin{eqnarray*}
(n-1)+ n + (n+1) &=& (n-1)\times n\times (n+1)\\
3n&=&n\times (n^2-1)\\
3 &=&n^2-1,
\end{eqnarray*}
\]

Post-scriptum

Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.

Crédits images

©JROBALLO / Adobestock

Commentaires

Al_louarn

février 3, 2024
10h48

1er défi

Soient $x_1 < x_2 x_1$ donc $7 – \frac{2X}{3} > 0$ et on en déduit que pour tout $n$, $y_n > x_n$ , et donc $x_n \neq 6$.

Finalement on doit choisir $x_2$ et $x_3$ tels que $2 \leq x_2 < x_3 \leq 5$ et $3 | (1 + x_2 + x_3)$. Il y a $\binom{4}{2} = 6$ combinaisons satisfaisant la première condition, dont seules les $2$ suivantes satisfont la seconde : $(x_1, x_2, x_3) = (1,2,3)$, d’où $X=6$, $y_n = x_n + 4$ et $(y_1, y_2, y_3) = (4,5,6)$. $(x_1, x_2, x_3) = (1,3,5)$, d’où $X=9$, $y_n = x_n + 1$ et $(y_1, y_2, y_3) = (2,4,6)$. Avec les $2$ solutions conjuguées, on a donc au total $4$ solutions, dont les sommes magiques sont respectivement $9, 10, 11, 12$ : __$1$__ _$6$_$5$_ $2$_$4$_$3$ __$1$__ _$6$_$4$_ $3$_$2$_$5$ __$2$__ _$5$_$3$_ $4$_$1$_$6$ __$4$__ _$3$_$2$_ $5$_$1$_$6$

ROUX

février 6, 2024
16h13

1er défi

J’ai décalé la suite de $4$.
J’ai donc
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
Je fait $0$ de trois manières, où les $+0$ et les $+1$ sous les chiffres de $-3$ à $+2$ indiquent que je ne le prends pas ou que je le prends.
Il faut que trois chiffres ne soient pris que deux fois et les trois autres chiffres une seule fois.
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
$+1$ $+0$ $+0$ $+0$ $+1$ $+1$
$+0$ $+1$ $+0$ $+1$ $+0$ $+1$
$+0$ $+0$ $+1$ $+1$ $+1$ $+0$
Pour faire $-1$, il suffit que je décale un nombre vers la gauche.
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
$+1$ $+0$ $+0$ $+1$ $+0$ $+1$
$+0$ $+1$ $+1$ $+0$ $+0$ $+1$
$+0$ $+1$ $+0$ $+1$ $+1$ $+0$
Pour faire $-2$, il suffit que je décale encore un nombre vers la gauche.
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
$+1$ $+0$ $+1$ $+0$ $+0$ $+1$
$+0$ $+1$ $+1$ $+0$ $+1$ $+0$
$+1$ $+0$ $+0$ $+1$ $+1$ $+0$
Pour faire $-3$, il suffit que je décale encore un nombre vers la gauche.
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
$+1$ $+1$ $+0$ $+0$ $+0$ $+1$
$+0$ $+1$ $+1$ $+1$ $+0$ $+0$
$+1$ $+0$ $+1$ $+0$ $+1$ $+0$
Pour faire $-4$, il suffit que je décale encore un nombre vers la gauche mais je ne peux le faire que de deux façons.
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
$+1$ $+1$ $+0$ $+0$ $+1$ $+0$
$+1$ $+0$ $+1$ $+1$ $+0$ $+0$
$+1$ $+1$ $+0$ $+0$ $+1$ $+0$
Pouvais-je faire trois fois $+1$ en décalant la première série vers la droite ? Non, seulement, deux façons.
$-3$ $-2$ $-1$ $+0$ $+1$ $+2$
$+0$ $+1$ $+0$ $+0$ $+1$ $+1$
$+0$ $+0$ $+1$ $+1$ $+0$ $+1$
$+0$ $+0$ $+1$ $+1$ $+0$ $+1$

Donc $4$ façons.

claude

février 9, 2024
8h44

2e défi

Soit abcd ce nombre,
On a 10c+d=5(10a+b)
10c est divisible par 5, donc d doit être également un multiple de 5.
Puisque c=6 on a donc
(6×10)+d=5k
Prenons k=1, alors (6×10)+d=65
Et donc 10a+b=65/5=13
abcd=1365

Nicolas RAVE

février 9, 2024
8h54

2e défi

X=1000a+100b+10c+d

10c+d=5(10a+b)

c=6

60+d=50a+5b

(a=0) impliquerait (d=0 ou 5 avec b>9) , ce qui est impossible

(a=1) implique (10+d=5b) qui implique (d=0 ou d=5), ces deux dernières implications impliquant ((d,b)=(0,2) ou (d,b)=(5,3))

X = 1260 ou 1365 conviennent.

(a > ou = 2) implique (d > ou = 100-60 +5b = 40 + 5b >9) , ce qui est impossible.

Donc X = 1260 ou 1365

Al_louan

février 9, 2024
11h25

Les chiffres doivent être distincts de 0 donc 1260 ne convient pas.

Connectez-vous pour répondre

Nicolas RAVE

février 9, 2024
11h42

2e défi

Bien vu.

Emporté par mon excès de formalisme courtois, j’ai failli à l’un des points, peut-être le principal, de ce défi, qui était de n’en manquer aucune information.

J’aurais dû ôter mes oeillères antizérophobiques.

Cela dit, ce défi pourrait finalement, puisqu’il n’impose pas de fournir un type d’approche qui servirait pour des contraintes plus complexes sur des nombres plus grands,
se remporter en osant affronter la terrible vérité selon laquelle 5*20=100.

Al_louarn

février 9, 2024
11h42

2e défi

Soit G le nombre formé des 2 chiffres de gauche, et D le nombre formé des 2 chiffres de droite. Le premier chiffre de D est 6. Et comme D = 5G il est multiple de 5, donc son dernier chiffre est 5 car 0 est interdit par l’énoncé. Donc D=65, puis G=D/5=13.

La réponse est donc $1365$.

claude

février 9, 2024
12h55

2e défi

A noter que :
Puisque (6×10)+d=5k
On a également pour k=3
60+15=75 et 75/5=15
Donc la 2° solution est : 1575
De même pour k=5
60+25=85 et 85/5=17
3° solution 1785
Et enfin la dernière pour k=7
60+35=95 et 95/5=19
4° solution 1995
Pour k>7 on obtient un nombre à 5 chiffres qui ne convient pas.
Les 4 solutions sont sont donc :
1365
1575
1785
1995

claude

février 9, 2024
13h00

claude

Oups ! Je me suis égaré
1 seule solution 1365, puisque c=6

Connectez-vous pour répondre

Al_louarn

février 16, 2024
8h18

3e défi

Une preuve sans mots :

$.$

Mario

février 17, 2024
13h25

3e défi

Autre proposition :
$.$

Al_louarn

février 17, 2024
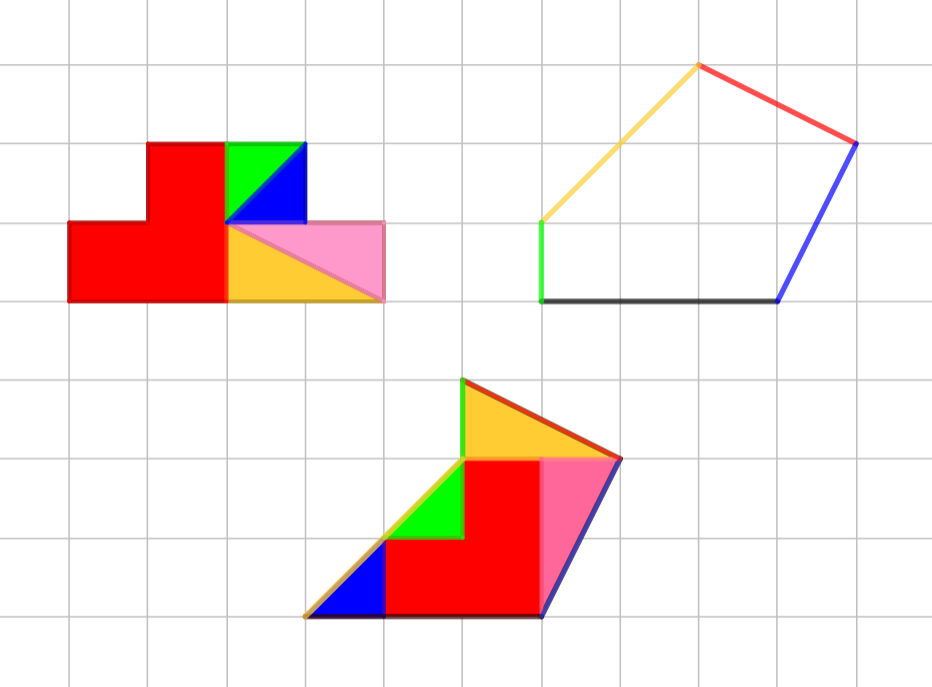
15h32

3e défi

Et une 3ème solution :
$.$

claude

février 23, 2024
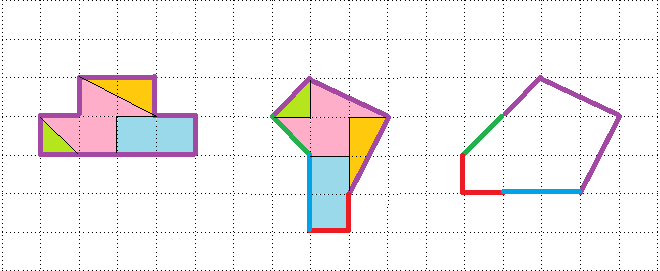
8h25

4e défi

Soit (a)+(a+1)+(a+2)=a(a+1)(a+2)
3a+3=a³+3a²+2a
D’où a³+3a²-a-3=0
On a 1 racine évidente a=1
a³+3a²-a-3=(a-1)(a²�3)
a³+3a²-a-3=(a-1)((a-1)(a+3)
Donc une seule Racine positive : a=1
D’où a²+(a+1)²+(a+2)²=14

Hébu

février 23, 2024
12h16

J’appelle $n-1, n, n+1$ mes trois nombres.

J’ai donc $(n-1)n(n+1)=3n$, soit $3n=n(n^2-1)$,
autrement dit $n^2-1=3$, $n^2=4$

Quant à la somme des carrés, c’est $3n^2+2$, soit 14

Connectez-vous pour répondre

Écrire un commentaire

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .

Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.

Défis de février 2024

Premier défi : le problème du mois

Solution du premier défi

Deuxième défi

Solution du deuxième défi

Troisième défi

Solution du troisième défi

Quatrième défi

Solution du quatrième défi

Post-scriptum

Crédits images

ÉCRIT PAR

Romain Joly

Commentaires

Écrire un commentaire