Courbe brachistochrone

• Courbe

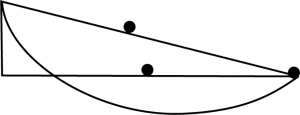
Si une particule est invitée à glisser sur une courbe dans un plan vertical, d’un point \(A\) à un point \(B\) plus bas, soumise uniquement à son poids, le temps requis pour effectuer la descente dépend de la forme de la courbe sur laquelle la particule glisse.
La droite \((AB)\) réalise la distance minimale mais ne réalise pas le temps minimal.

Ce problème apparait en 1633 chez Galilée qui écrit : « Il semble possible de conclure que le mouvement le plus rapide entre deux points n’a pas lieu le long de la ligne la plus courte, c’est-à-dire le long d’une droite, mais le long d’un arc de cercle » ¹Galilée. {Discours concernant deux sciences nouvelles}, (th. XXII, prop. XXXVI), (1633). Rééd. PUF, 1995.[\mfn].

Jean Bernoulli pose clairement le problème en 1696 et des solutions furent aussitôt apportées par lui-même, par son frère Jacques Bernoulli, Newton, Leibniz, …
La courbe qui réalise ce temps minimal dite {brachistochrone} (terme utilisé par Jean Bernoulli), du grec {brakhisto} (le plus court) et {chronos} (temps) est définie par la représentation paramétrique
\[
x(t) \; = \; a({t}-sin{t}), \qquad {y(t)} \; = \; {-a}(1-cos{t})
\]
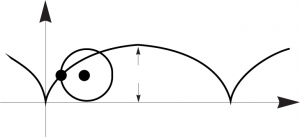
(où \(2{a}\) est la perte d’altitude par rapport au point de départ) et s’appelle cycloïde (ici une cycloïde renversée et telle que la verticale en \(A\) est tangente à la courbe). Une cycloïde est la courbe décrite par un point fixé sur un cercle (de diamètre \(2{a}\)) qui roule sans glisser sur une droite ¹Voir aussi le beau billet  de Michèle Audin .

Pour trouver sa solution, au lieu d’une particule soumise à son poids, Jean Bernoulli considéra un rayon de lumière traversant différents milieux ²Voir la page de Paul Kunkel. . La vitesse de la lumière dépend du milieu traversé. Lorsqu’elle traverse la frontière d’un milieu à un autre elle est réfractée. Le principe de Fermat établit que lorsque la lumière traverse la frontière d’un point à un autre elle suit le chemin le plus rapide. La recherche des méthodes pour résoudre le problème de la courbe brachistochrone a donné naissance à ce qu’on appelle en Mathématique Le calcul des variations. On trouve des solutions détaillées à ce problème, par exemple, dans ³Page associée sur.https://mathcurve.com/courbes2d/brachistochrone/brachistochrone.shtml. et ⁴Page associée sur Wolfram MathWorld.

La cycloïde (telle que les points de rebroussement soient vers le haut) jouit aussi de deux autres propriétés : elle est isochrone (la particule lâchée sur une arche a un mouvement périodique dont la période est indépendante du point où on lâche la particule), et elle est tautochrone (le temps nécessaire pour atteindre B est indépendant du point de la courbe d’où on lâche la particule avec une vitesse initiale nulle).

Références

John C. BRIXEY, Richard V.ANDREE. Fundamentals of College Mathematics. Holt, Rinehart and Winston, Inc. 1961.

Galilée. Discours concernant deux sciences nouvelles, (th. XXII, prop. XXXVI), (1633). Rééd. PUF, 1995.

V. GUTENMACHER, N. B. VASILYEV. Lines and Curves. Birkhäuser Boston, Inc. 2004.