Il y a des formules qui sonnent bien, qui semblent prendre sens tout naturellement dans la tête de tout un chacun. Parfois même on a le sentiment d’atteindre une notion subtile, de comprendre une idée fine, seulement en écoutant un mot, une tournure de phrase, un qualificatif. Ce phénomène est amplifié par un usage répété quotidien. Il devient même presque impensable qu’on puisse s’interroger sur le sens de mots tellement c’est évident !
Le premier exemple est le qualificatif « exponentiel ». On entend dans les médias parler de croissance exponentielle. J’ai demandé autour de moi si mon capital placé sur un livret A à un taux de 1,25% suivait lui aussi une croissance exponentielle. On a ri de ma remarque : « pour que ce soit exponentiel, il faut que ça rapporte beaucoup et très vite ». Alors, je devais arrêter de m’efforcer de faire comprendre ce que signifiait « exponentiel » dans le jargon mathématique et plutôt tenter de constituer un dictionnaire pour parvenir à échanger. Ainsi, exponentiel signifiera rapide, fort. Ne cherchez pas plus de précisions ou une allusion à une loi qui indiquerait dans une échelle asymptotique un type de croissance. Mais comme tout le monde en parle, c’est bien clair dans la tête de chacun.
Le second exemple est dans la même veine. Le mot « proportionnel ». On peut entendre dans les propos d’une même personne d’une part que le montant des impôts est proportionnel aux revenus et que d’autre part, plus on gagne d’argent plus le taux d’imposition est fort. Ici, c’est encore plus vicieux car on fait un usage massif de la correspondance linéaire, nous vivons dans le monde du pourcentage. Et pourtant, on emploie l’adjectif « proportionnel » pour dire autre chose. Car dans le dictionnaire que je suggère, à l’entrée « proportionnel » on trouve « fonction croissante de ». Rien de plus précis, pas de sous-entendu de l’existence d’un coefficient de proportionnalité, non, il peut changer. Alors on pourrait dire affine par morceau, mais non, on dit proportionnel simplement pour « croissant ». Et même « inversement proportionnel » pour « décroissant », pas d’allusion ici non plus à une quelconque loi en 1/x.
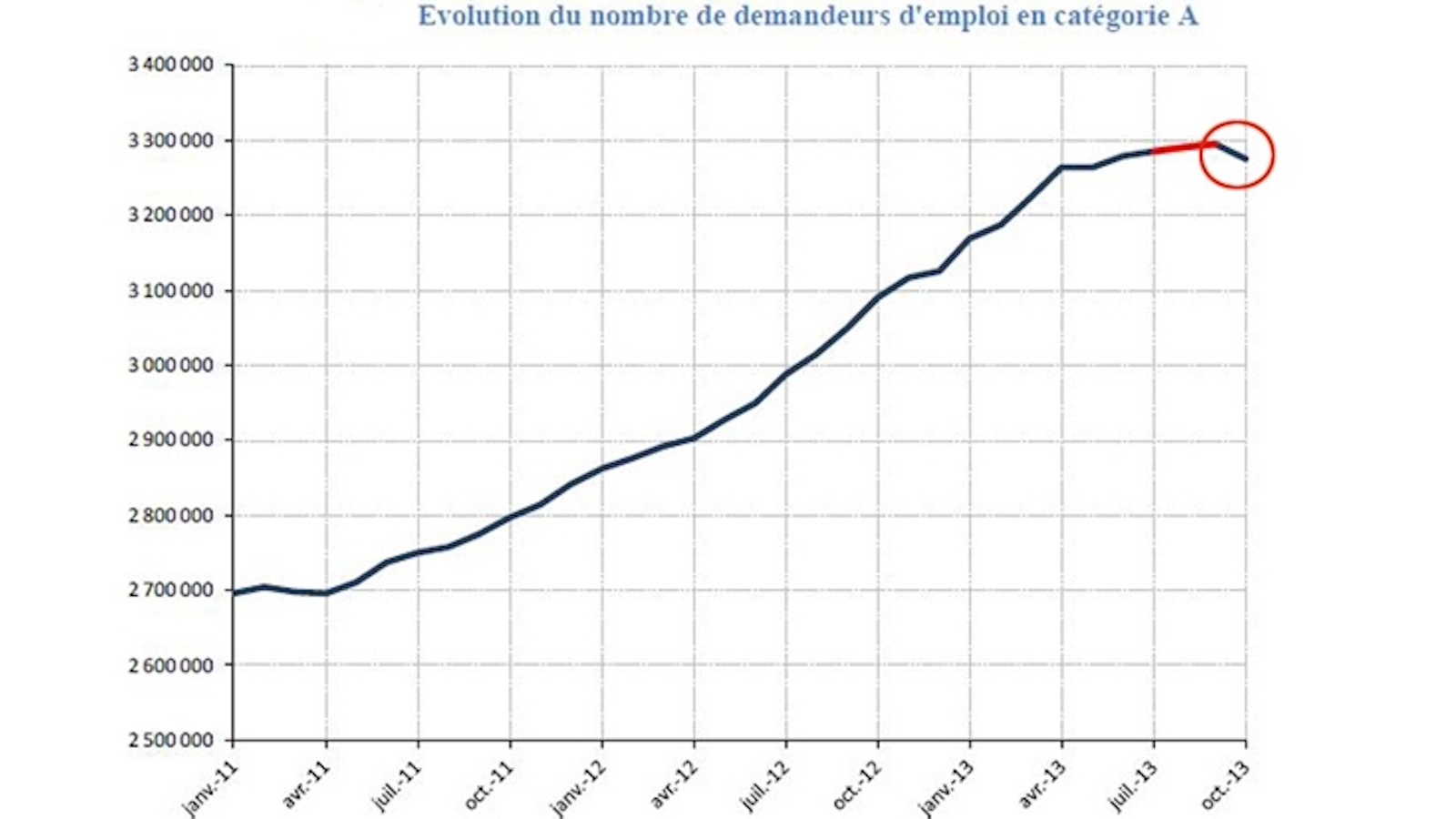
Enfin, pour rebondir sur l’inversion, pourquoi ne tenterions-nous pas d’inverser les courbes ? C’est un défi présidentiel que de parvenir à inverser la courbe du chômage. Partirait-elle vers la gauche désormais, en remontant le temps ? Non. Il faut peut-être inverser la croissance exponentielle pour obtenir une décroissance (exponentielle toujours) ? Non. C’est ça, il faut seulement stopper la croissance : borner supérieurement alors, majorer quoi ? Pas plus de 3.5 millions de chômeurs par exemple. Dans mon dictionnaire, il y a une variante pour cette entrée-là. Car certains voient localement que la courbe est en train de s’inverser. Alors c’est bien de courbure qu’il s’agit et l’expression « inverser la courbe » est donc une contraction d’inverser la courbure de la courbe. La courbe peut rester croissante, mais passe sous sa tangente, à partir de ce moment là, l’augmentation instantanée n’est plus croissante : c’est déjà ça ! Tout cela me semble cohérent, si la courbe est croissante et convexe, inverser c’est majorer et viendra bien le moment où la courbure elle aussi s’inversera !


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.