Un atelier sur les fractales au collège

• Algorithme
• Fractale

• Ressources pédagogiques

Du 13 au 17 novembre 2023 s’est tenue la semaine des sciences du collège de Bons-en-Chablais.

Ce billet propose un résumé de cette semaine et d’un atelier en mathématiques sur le thème des fractales (au travers de l’exemple de l’éponge de Menger), en espérant que cela puisse susciter de nouvelles idées dans d’autres établissements. Cet atelier ayant déjà été réalisé plusieurs fois, il existe de nombreux documents explicatifs pour facilement le mettre en place.

Différentes matières abordées

On ne parlera ensuite que d’un atelier de maths parmi les autres, mais cette semaine a permis aux élèves de participer à beaucoup d’autres choses : entrer dans un planétarium gonflable, voir plusieurs expositions prêtées au collège (en biologie et chimie), rencontrer un auteur de bandes dessinées, en savoir plus sur les risques d’inondations, visionner des films, discuter avec une archéozoologue et manipuler un squelette de vache, découvrir la fabrique de bruits animaux, participer à des jeux de stratégie, réaliser une fresque du climat, aborder les questions de l’énergie et du développement durable, participer à un atelier de philosophie et en apprendre plus sur l’art engagé pour l’écologie. En plus de ces activités qui peuvent être vues comme éloignées du programme du collège, l’équipe pédagogique en a profité pour proposer des travaux pratiques de sciences en demi-groupe et des ateliers de programmation.

Concernant les mathématiques, trois interventions ont été faites : un escape game, une pièce de théâtre appelée Very math trip et un atelier “fractale”.

Un atelier “fractale” inspiré du projet MegaMenger

La notion de fractale ¹Voir le billet Fractales, points fixes et coquillages. fut introduite au vingtième siècle par Benoît Mandelbrot ²Voir le portrait de Benoît Mandelbrot.. Ces ensembles géométriques relativement contre-intuitifs sont souvent décrits par une méthode de construction algorithmique – on répète “une infinité de fois” une opération simple – et mènent à d’impressionnantes représentations graphiques ³Voir l’article La méthode de Newton et son fractal…en 3D !.

L’éponge de Menger, introduite par Karl Menger, en est un exemple. Ici, l’état de départ est un grand cube qu’on appellera éponge de niveau zéro. Pour passer à l’étape suivante, l’éponge de niveau un, on divise ce grand cube en vingt-sept petits cubes de côtés trois fois plus petits et on retire les petits cubes qui ne laissent apparaître qu’une face ou aucune, c’est-à-dire les sept cubes que l’on pourrait dire centraux. Pour passer à l’étape suivante, l’éponge de niveau deux, on creuse ainsi chacun des vingt petits cubes restants composant l’éponge de niveau un. Pour passer à une éponge de niveau \(n+1\) on creuse ainsi chacun des \(20n\) petits cubes composant l’éponge de niveau \(n\). En poursuivant ce processus “à l’infini”, on obtient une éponge de Menger.

Bien qu’il s’agisse d’une figure en trois dimensions ayant visiblement une certaine épaisseur, elle est en fait d’un volume nul (mais son volume est bien défini, contrairement à d’autres figures un peu plus abstraites). La question de sa représentation est d’autant plus intéressante que, dans les années 90, l’ingénieure Jeannine Mosely proposa une méthode très efficace pour en réaliser en trois dimensions à l’aide de cartes cartonnées pliées ⁴Voir ici..
En 2014, vingt établissements autour de la planète se sont mobilisés pour construire des répliques de l’éponge de Menger à l’aide de cette méthode. Vous trouverez sur leur site dans la section “Downloads” de nombreuses ressources en anglais présentant le projet et la méthode de construction. Le projet MegaMenger fut ensuite repris par l’Université de Genève qui produisit pour l’occasion un tutoriel en français – en libre accès sur leur site – expliquant comment construire votre propre représentation de la fractale. Il s’agit d’un travail utilement abordable par des élèves de collège. Notre représentation de l’éponge de Menger consiste en une éponge de niveau aussi élevé que possible que nous construirons non pas en creusant un grand cube de départ mais en assemblant de petits cubes, chacun construit avec six cartes de visite pliées, sans colle et sans ciseau mais très solide. On donne dans le tableau ci-dessous le nombre de petits cubes et de cartes de visite nécessaires pour construire les premiers niveaux d’une éponge. Notons \(l\) la largeur d’une carte.

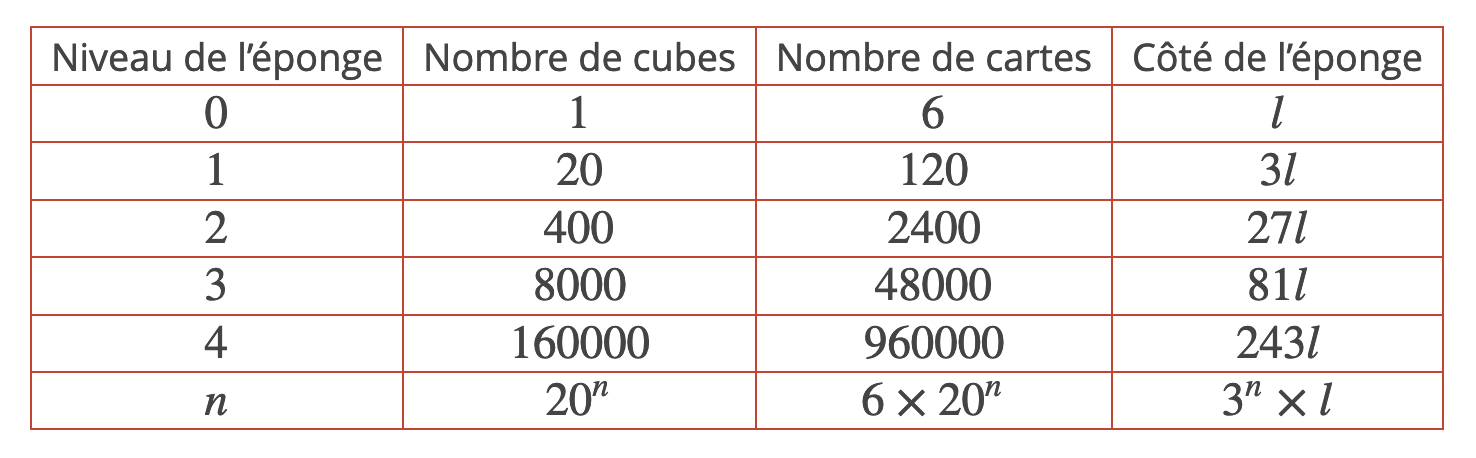
Comme on peut le constater sur ces premiers exemples, il existe une nette différence entre deux éponges de niveaux successifs. Ainsi, dans le cadre de la semaine des sciences, il était tout à fait raisonnable d’atteindre le niveau deux et illusoire d’espérer le niveau quatre. Le niveau trois constituait un défi sérieux et exigeant pour les sept cents élèves du collège de Bons-en-Chablais.

Aborder le thème des fractales avec des enfants

En plus de la question de l’infini, l’éponge de Menger permet d’aborder de façon relativement concrète des notions géométriques (surface et volume) et de combinatoire (combien de cubes dans une éponge d’un niveau donné) qui peuvent être reliées au programme de collège. Par ailleurs, le faire sous la forme d’un atelier de fabrication d’une éponge en papier est un travail de groupe pouvant mobiliser autant d’élèves qu’on le souhaite à condition d’avoir l’espace, le temps, le matériel et l’organisation requise. Lors de la semaine des sciences du collège de Bons-en-Chablais, l’atelier a été en moyenne très apprécié des enfants et permettait de leur laisser une certaine liberté d’organisation.

 

Organisation dans un collège

Matériel

● Cartes (de visite). Il s’agit du seul élément essentiel. Il en faut suffisamment pour construire le niveau d’éponge visé (se reporter au tableau ci-dessus). Elles doivent être suffisamment rigides, de format rectangulaire et toutes exactement de même largeur. Le format “carte de visite” \(85\)mm\(\times 55\)mm convient très bien. De nombreuses cartes se perdent ou sont mal pliées : pensez à prendre suffisamment de marge. Pour trouver suffisamment de cartes gratuitement, n’hésitez pas à demander à récupérer des cartes de professionnels (et entreprises) ou des restes auprès d’imprimeries (vous les débarrasserez parfois de cartes qui allaient être jetées).

● Fiche technique. Vous en trouverez une très bien réalisée sur le site de l’Université de Genève.

● Décoration. Vous pouvez décorer les cubes extérieurs avec des motifs de tapis de Sierpiński ⁵Voir ici. sur les faces visibles des cubes. Vous pouvez trouver l’un des motifs utilisés dans le projet MegaMenger ici.

● Scotch. Théoriquement, la méthode de pliage mentionnée ci-dessus ne nécessite aucun collage. Toutefois, des pliages de cartes et des assemblages de cubes imparfaits peuvent rapidement créer des fragilités et il peut être utile de renforcer certaines éponges avec du scotch (attention à ne pas bloquer les languettes utiles en le faisant). Du scotch de bureau transparent fonctionne très bien.

● Grandes plaques. À partir du niveau deux, les éponges peuvent devenir difficiles à manipuler et, en particulier, à transporter. Il peut être utile de prévoir de grandes plaques (en bois par exemple) suffisamment larges pour y poser vos cubes et les déplacer.

Espace

● Un lieu d’assemblage avec des tables pour les petites éponges. Les élèves doivent pouvoir manipuler confortablement, avoir une surface plane pour plier les cartes et assembler correctement les éponges de niveau zéro et un.

● Un lieu d’assemblage pour les grandes éponges. A partir du niveau deux, il est parfois plus pratique de manipuler au sol (sur une grande plaque pour ensuite pouvoir déplacer la construction).

● Un lieu de stockage. Il faut pouvoir stocker les cartes pliées et les éponges en attendant de les intégrer à la structure finale.

● L’agencement des tables et des lieux de manipulation doit laisser suffisamment d’espace pour que les élèves puissent circuler sans heurter les éponges.

● Si vous prévoyez de déplacer la structure finale, pensez à vérifier que celle-ci passera les portes. Pour calculer la taille d’une éponge, reportez-vous au tableau ci-dessus.

Quelques problèmes rencontrés

● Les cartes étaient souvent mal pliées. Il a souvent fallu répéter aux élèves de bien respecter la largeur des cartes et de plier à plat sur les tables (et non en l’air devant eux ou sur leurs jambes).

● La méthode d’assemblage par couronnes des éponges de niveau un (fonctionnant de la même façon pour les niveaux supérieurs) présentée dans le document de l’Université de Genève n’était souvent pas respectée et empêchait de construire correctement.

Lors de la semaine des sciences du collège de Bons-en-Chablais, nous avons facilement pu mettre en place un atelier réalisé en demi-groupe (environ quinze élèves). Nous commencions par un exposé de vingt minutes avec diaporama pour aborder la notion de fractale et présenter le projet aux élèves, en mentionnant la technique de pliage et en montrant un exemple plié d’éponge de niveau un. Ensuite, nous passions dans la salle dédiée à la manipulation avec deux encadrants pour leur présenter plus en détails la méthode d’assemblage des cartes et pour les laisser manipuler (plus ou moins longtemps selon leur âge). La presse locale est venue couvrir le projet et cela fut très valorisant pour les enfants.