
Les mathématiciens de la période de l’hégémonie arabe (8e – 13e siècle) qui ont contribué d’une façon originale à la théorie des équations, ont aussi expliqué et justifié leurs méthodes géométriquement. À certains types d’équations, ils n’ont donné que des solutions géométriques.
Par exemple, pour résoudre l’équation
\[x^2+10x=39\]
qui traduit l’énoncé : « Un carré et dix de sa racine sont égaux à neuf et trente », El Khawarizmi (783-850) donne la méthode géométrique suivante.
Désignons par \(AB\) la valeur de l’inconnue \(x\). Construisons le carré \(ABCD\) (fig.1).
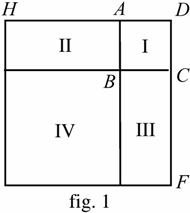
fig.1
Prolongeons \(DA\) à \(H\) et \(DC\) à \(F\) tels que \(AH=CF=5\) qui est la moitié du coefficient de \(x\).
Complétons le carré sur \(DH\) et \(DF\). Alors les aires des domaines I, II et III sont respectivement \(x^2\), \(5x\) et \(5x\). Leur somme est le premier membre de notre équation.
On ajoute à présent aux deux membres l’aire IV qui vaut \(25\). Donc l’aire du carré entier est \(39+25=64\) et son côté est égal à \(8\).
Donc \(AB\) ou \(AD\) est égal à \(8-5=3\). C’est la valeur désirée de \(x\).
Les mathématiciens de cette époque ont aussi résolu des équations cubiques algébriquement et donné une interprétation géométrique comme celle fournie pour les équations quadratiques. C’est ce qu’ont fait par exemple Thabit Ibn Qurra(826-901) et El Hassen Ibn El Heythem (965-1039).
Quant au remarquable Omar El Kheyyam (1048-1131), il affirme que l’équation générale du troisième degré peut être résolue géométriquement en utilisant les coniques (il croyait faussement à l’impossibilité de la résoudre algébriquement, ce qui ne se fera que des siècles plus tard). Sa célébrité, comme mathématicien, repose donc surtout sur le fait qu’il est le premier à avoir étudié les équations cubiques ayant une racine positive, d’une manière exhaustive. Dans ce contexte il dit : « … Moi au contraire, je n’ai jamais cessé de désirer vivement de faire connaître avec exactitude toutes les espèces, les possibles avec les impossibles en me fondant sur des démonstrations » ([2] p. 25). Dans ce qui suit on illustre la méthode qu’il utilise dans son traité d’algèbre (ca. 1079) pour résoudre plusieurs types d’équations cubiques en prenant l’un des cas les plus simples de ce qu’il a traité, en l’occurrence l’équation
\[x^3+Bx=C\]
où \(B\) et \(C\) sont positifs. ([3]. p. 192-195)
El Kheyyam écrit l’équation sous la forme
\[x^3+b^2x=b^2c\]
avec \(b^2=B\) et \(b^2c=C.\)
Il construit ensuite la parabole dont le latus rectum 1Du latin latus : « côté » et rectum : « droit ». C’est la corde focale qui est perpendiculaire à l’axe de la parabole. est b 2Cette valeur fixe en effet la parabole qui, cependant n’est pas constructible à l’aide de la règle et du compas. Le paramètre étant \(p=\frac{b}{2}\), le foyer \(F(0, \frac{b}{4})\) et la directrice \(D: y=-\frac{b}{4}\).. (fig.2)
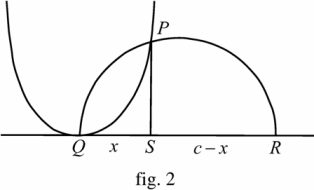
fig.2
Il construit ensuite le demi-cercle de diamètre \(QR\) de longueur \(c\). Alors le point \(P\) commun à la parabole et au demi-cercle détermine la perpendiculaire \(PS\), et \(QS\) est « la solution » de l’équation proposée.
Comme on peut le constater de l’équation \(x^2=by\) de la parabole, on a
\(x^2=b.PS\) (1)
\(\frac{b}{x}=\frac{x}{PS}\). (2)
Dans le triangle rectangle \(QPR\) la hauteur \(PS\) est la moyenne proportionnelle de \(QS\) et \(SR\). Donc
\(\frac{x}{PS}=\frac{PS}{c-x}.\)(3)
De (2) et (3) il vient :
\(\frac{b}{x}=\frac{PS}{c-x}.\)(4)
Mais de (2) on a \(PS=\frac{x^2}{b}.\)
Si on substitue cette valeur de \(PS\) dans (4) on voit sans peine que \(x\) satisfait l’équation
\[x^3+b^2x=b^2c.\]
El Kheyyam résout également l’équation
\[x^3+ax^2=c^3\]
dont les racines sont déterminées par l’intersection d’une hyperbole et d’une parabole. Il fait de même pour les équations
\[x^3+ax^2+b^2x=b^2c\]
et
\[x^3-ax^2+b^2x=b^2c\]
dont les racines se déterminent par l’intersection d’une ellipse et d’une hyperbole (cf.[2] p.27-29).
El Kheyyam résout aussi l’équation du 4ème degré
\[(100-x^2)(10-x)^2=8100\]
dont les solutions (positives) sont données par l’intersection d’une hyperbole et d’un cercle.
La résolution des équations cubiques en utilisant l’intersection de coniques était l’un des plus grands pas des mathématiciens de cette période en algèbre.
Références
Jean-Paul Colette histoire des mathématiques tome 1, Éditions du Renouveau Pédagogique Inc., Canada, 1973.
Julian Lowell Coolidge The Mathematics of Great Amateurs, Clarendon Press . Oxford, 1990.
retour
Morris Kline Mathematical Thought from Ancient to Modern Times, Volume 1, Oxford University Press, 1990.
retour
Reviel Netz The Transformation of Mathematics in the Early Mediterranean World. From Problems to Equations, Cambridge University Press, 2004.
On peut aussi jeter un coup d’œil ici.


11h41
Merci pour ce billet qui fait toucher du doigt plusieurs points subtils. Peut-être pouvez-vous dire quelques mots sur le but de la résolution des équations algébriques pour ces mathématiciens ?
En effet l’analyse géométrique de la première équation fournit bien une solution explicite (à partir d’une figure… hypothétique puisque son tracé suppose connue la valeur de l’inconnue !) tandis que, pour la seconde équation, on doit d’abord transformer les coefficients et vous précisez que la parabole n’est pas constructible (à la règle et au compas). L’objectif est-il donc de fournir une procédure donnant un résultat numérique ? de s’assurer de l’existence d’une solution positive ?
Encore merci.
10h12
Merci Jérôme pour ce commentaire.
Effectivement, ces mathématiciens, qui ont continué d’une façon générale le travail des mathématiciens Grecs et Hindous, ont cherché des résultats numériques à des problèmes d’astronomie, d’astrologie, d’optique (en particulier pour les équations), de distribution, d’héritage, de commerce, de mesure de terrains, …
Leur but n’était pas les aspects trop théoriques mais plutôt le développement de sujets plus conformes à leur approche pratique.
15h41
L’histoire des sciences nous montres que les grands theories mathematiques se caché toujours derriéres des questions appliquées de nature divers. Malheuresement les travaux des mathematiciens musulmans n’a pas eu de continuité