
Suite au billet, d’Etienne Ghys sur l’appel à la loi gaussienne pour dénoncer les fraudes à la dernière élection législatives en Russie, il est tentant de se poser les mêmes questions sur le système électoral en France.
Pour rappel, le samedi 10 décembre des milliers de russes manifestaient pour protester contre la fraude présumée aux élections législatives du 4 décembre. Certains manifestants affirmaient que les résultats officiels des élections sont hautement improbables au regard de la loi gaussienne. Il est donc naturel de regarder la situation française.
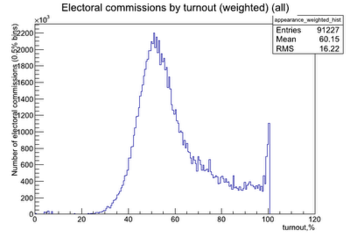
.
La première question qui se pose est le choix de l’élection. Les dernières législatives ont eu lieu les 10 et 17 juin 2007 (les prochaines se déroulant les 10 et 17 juin 2012) mais le système à deux tours rend difficile la comparaison avec l’élection russe, car certains partis comme les écologistes ou le front national ne présentent pas des candidats dans toutes les circonscriptions. Les élections européennes ne sont qu’à un tour (7 juin 2009 pour les dernières) mais ne déchaîne qu’assez peu les passions ( d’où 59.37% d’abstention). La primaire socialiste est un cas intéressant et les résultats sont disponibles par bureau de vote mais comme il n’y a pas le nombre d’inscrits il est difficile d’étudier la participation. On pourrait avoir envie d’extrapoler à partir d’élections antérieures mais cela semble très hasardeux car il y a eu 1.7 millions d’inscriptions en 2011 (sur 43.2 millions d’électeurs, voir ici). Nous allons donc regarder le premier tour de la dernière élection présidentielle (22 avril 2007).
Notons que les résultats ne sont sur la Plateforme française d’ouverture des données publiques Open Data qu’au niveau de la commune. Ceci est étonnant car le ministère de l’intérieur possède (évidemment) des fichiers et qu’ils ont été mis à disposition du public par le site NosDonnees.fr.
Commençons par une rapide description des données. 36 704 366 votants (sur 43 319 652 inscrits) ont voté pour l’un des douze candidats dans l’un des 65 617 bureaux de vote. Ceci représente donc une participation de 84.73 %.
La première idée pour représenter la participation des bureaux de vote est de construire l’histogramme, c’est-à-dire que l’on découpe l’intervalle [0,1] en \(m\) classes et la surface d’une classe est proportionnelle au nombre d’occurrence de la classe (concrètement la surface est proportionnelle aux nombre de bureaux de vote ayant une participation comprise entre les bornes de la classe). Par analogie avec le diagramme présenté lors des manifestations (voir ci-dessus), il est naturel d’utiliser un estimateur plus fin de la densité et nous avons donc choisi un estimateur à noyau, qui donne une estimation plus lisse. Formellement nous avons
\[\hat f_h(x)=\frac{1}{Nh}\sum_{i=1}^NK\left(\frac{x-x_i}{h}\right)\]
où \(x_i\) représente les pourcentages dans les bureaux de vote, \(h\) un paramètre nommé fenêtre, qui régit le degré de lissage de l’estimation et \(K(.)\), un noyau (kernel en anglais). Le plus souvent, \(K(.)\) est choisi comme étant la densité d’une fonction gaussienne standard (espérance nulle et variance unitaire).
Nous ne commenterons pas le fait que, pour l’élection russe, l’axe des abcisses dépasse les 100% semblant indiquer, soit un problème d’échelle, soit des bureaux de vote ayant voté à plus de 100%.
La figure ci-dessous représente donc la densité de la participation aux élections présidentielles
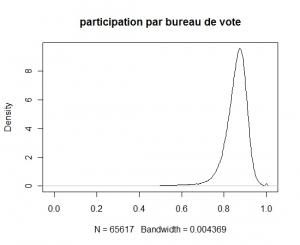
.
Un coup d’oeil rapide peut trouver ce graphe satisfaisant par sa forme général. Une allure plutôt symétrique et piqué vers 85% semble rassurant. Cependant la bosse à 100% est intrigant car il indique que 116 bureaux de vote ont une participation de 100% (alors que 125 bureaux ont une participation d’au moins 99% et à l’autre extrémité 2 bureaux de vote n’ont vu aucun votant).
Même si le phénomène est de bien moins grande amplitude que dans le cas russe, il est tentant de chercher à comprendre. Les résultats des différents candidats étant assez proches des résultats nationaux et les 116 bureaux de vote étant bien répartis sur le territoire il est difficile de croire à un bourrage d’urnes.
Selon le ministère de l’intérieur un bureau de vote représente de 800 à 1000 électeurs. En pratique le plus petit bureau de vote était à Bordères-Louron (dept 65) avec 5 inscrits (et 5 votants), le plus grand était à Barbentane (dept 13) avec 2962 inscrits (et 2531 votants). En moyenne il y a 660 inscrits par bureau de vote (et une médiane de 708 inscrits).
La figure ci-dessous montre un estimateur de la densité de la taille des bureaux de vote et il y a clairement un aspect bimodal. Il est tentant de penser que cela correspond aux petites et aux grandes villes mais c’est assez difficile à vérifier pour plusieurs raisons :
- (i) les arrondissements ne sont pas précisés dans les chiffres du ministère de l’intérieur (les bureaux de vote ne sont même pas géolocalisés en France),
- (ii) les données de recensement sont par code géographiques.
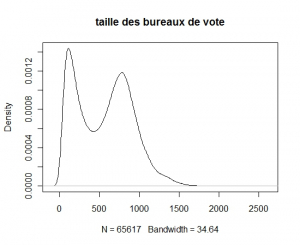
.
La probabilité d’avoir 100% des votants dépend donc fortement de la taille du bureau de vote. Au vu du graphe précédent nous pouvons représenter la densité des participations pour les petits bureaux de vote et pour les gros bureaux de vote (en zoomant un peu sur la partie droite de la distribution
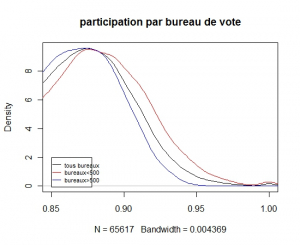
.
Et la bosse s’explique enfin.
A ce stade il apparait donc nettement que la loi normale n’a rien de naturel même si le pic présenté lors des manifestations russes est sensiblement plus marqué.
Pour terminer regardons un petit problème de boules dans une urne.
Considérons une urne avec une boule blanche et une boule noire. Tirons une balle au hasard dans l’urne, notons la couleur et remettons la boule dans l’urne. Après un grand nombre de tels essais indépendants, la distribution de la fraction de boules blanches sera gaussienne. La couleur de la boule tirée ne dépend pas du tirage précédent et nous avons donc indépendance des tirages. Ceci revient à dire que les électeurs choisissent leurs opinions politiques, indépendamment de leurs voisins, collègues et amis. Pour tenir compte des événements dépendants, Markov a proposé la modification suivante. L’urne contient initialement une boule blanche et une noire. On tire une boule au hasard, on note la couleur, on la remet dans l’urne et on rajoute une boule de la couleur de la boule tirée. Après deux essais, nous avons pu sortir soit deux boules noires, soit deux boules blanchess soit une boule noire et une boule blanche. Un calcul de combinatoire simple montre que ces trois combinaisons sont équiprobables. Il est facile de montrer par récurrence qu’à l’issue de \(N\) tirages, on peut avoir \(0,1,\ldots,N\) boules blanches et tous ces événements sont équiprobables.
Quelle relation ce modèle peut-il avoir avec les élections ? Prenons le modèle suivant. Dans une ville, qui n’a qu’un seul bureau de vote, au début, il y a deux supporters pour chaque candidat. L’un représente le candidat boule blanche et l’autre le candidat boule noire. Chacun d’eux commence à faire campagne pour son candidat. Lorsque le supporter persuade à quelqu’un de rejoindre à son clan, le nouveau venu fait aussi campagne. Si nous supposons que chaque supporter a des chances égales de réussir à recruter un nouveau supporter, nous sommes exactement dans le modèle de Markov. Cela signifie que la répartition en pourcentage des voix des bureaux de votene doit pas être gaussienne, mais uniforme. Bien sûr, le modèle que nous venons de considérer est simpliste et néglige les interactions personnelles.
Dans l’image ci-dessous (qui vient d’ici) et qui sert de logo au billet d’Etienne, la courbe marron n’est pas très loin de l’uniforme.

.
Ce qui est assez différent de ce qu’on observe si on regarde la distribution des candidats au premier tour en France
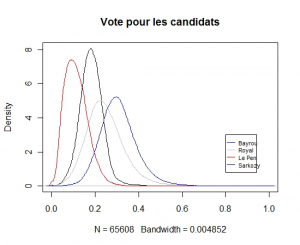
.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.