
Défi
Étant donné un cercle, construire un carré inscrit dans ce cercle en 7 actions maximum à la règle (non graduée) et au compas.


La construction en 7 étapes
Soit \(\Omega\) le cercle de centre \(O\) et de rayon \(r\) et \(A\in \Omega\).
- Tracer \(C_1\) le cercle de centre \(A\) de rayon \(r\). Il coupe le cercle \(\Omega\) en \(A_1\) et \(A_2\).
- Tracer \(C_2\) le cercle de centre \(A_1\) qui passe par \(A_2\). Il coupe \(\Omega\) en \(B\).
- Tracer la droite \(d_1=(OA_1)\). Elle coupe \(C_2\) en \(A_3\) et en \(A_4\) avec \(A_4\) le point à l’intérieur du cercle.
- Tracer la droite \(d_2=(BA_3)\). Elle coupe \(\Omega\) en \(C\).
- Tracer la droite \(d_3=(BA_4)\). Elle coupe \(\Omega\) en \(D\).
- Tracer [AC].
- Tracer [AD].
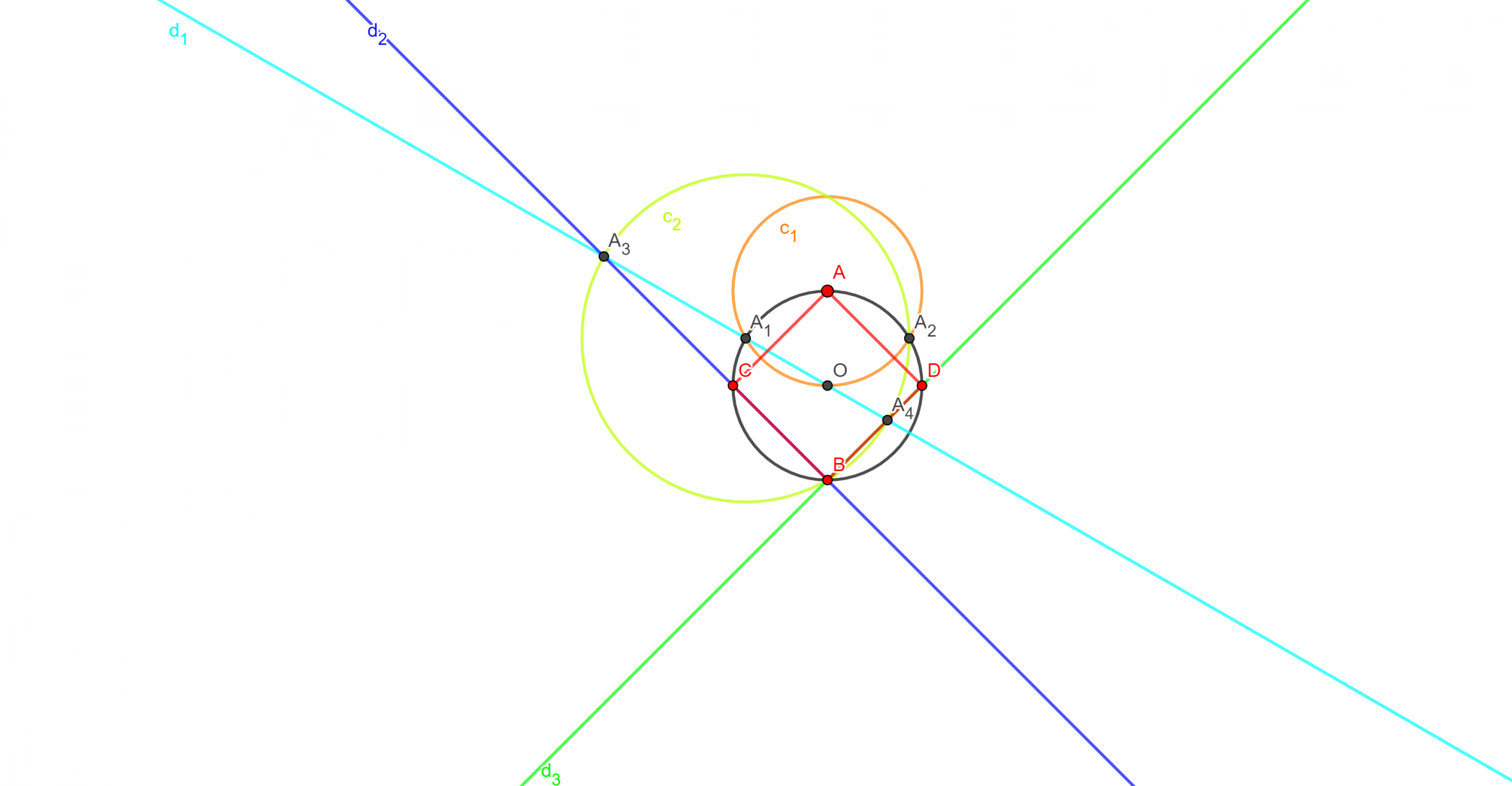
.


Démonstration par calcul d'angles
Rappel (Théorème de l’angle au centre) : Dans un cercle, un angle inscrit est un angle dont le sommet est sur le cercle et dont les côtés coupent le cercle et un angle au centre est un angle dont le sommet est le centre du cercle et dont les côtés coupent le cercle. Si un angle inscrit et un angle au centre interceptent le même arc, alors l’angle au centre mesure le double de l’angle inscrit.
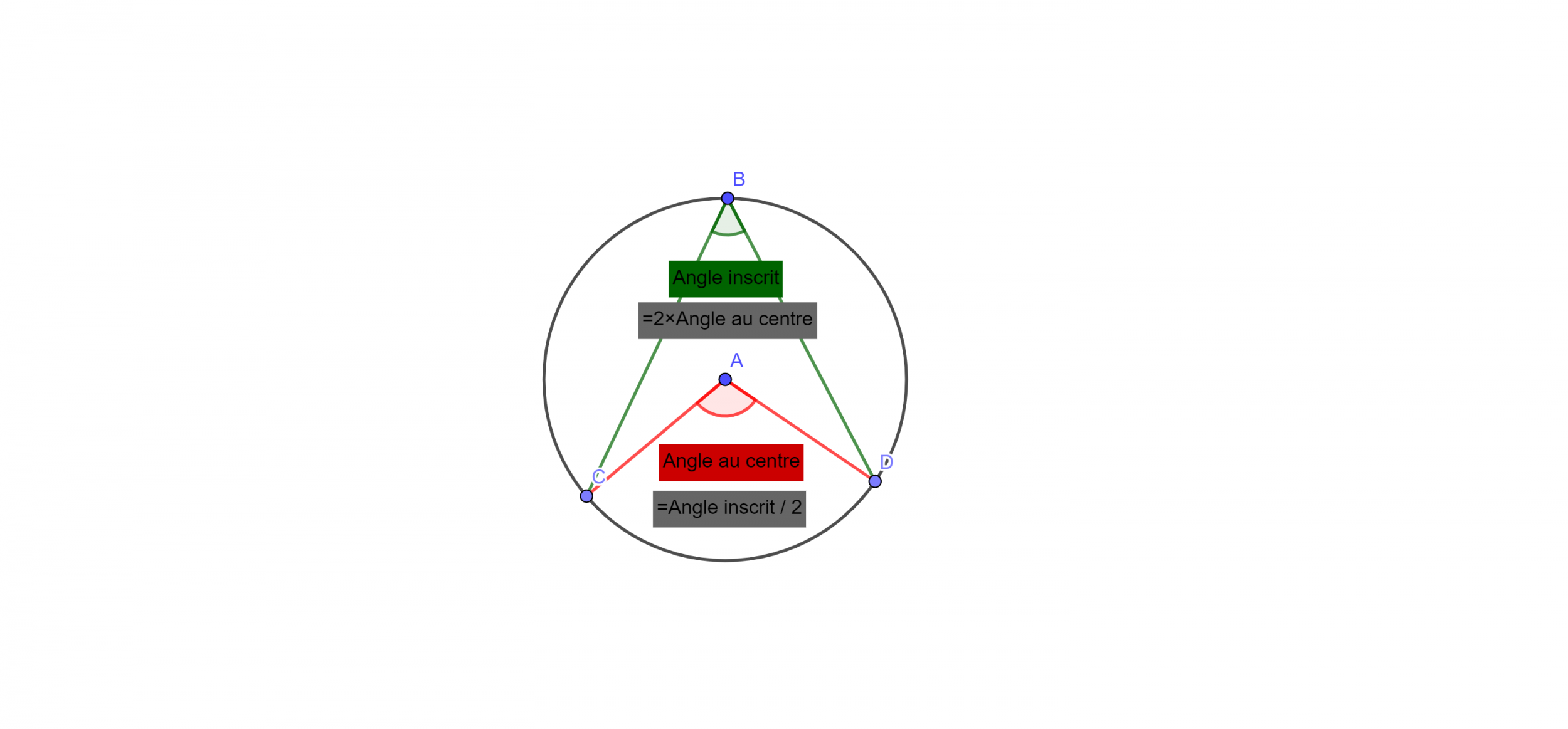
.
On suppose que \(ABCD\) est un rectangle.
1. Les angles \(\widehat{AOA_1}\) et \(\widehat{BOA_4}\) étant opposés par le sommet, que vaut l’angle \(\widehat{BOA_4}\) ?
Indication : Trouver la nature du triangle \(AOA_1\)
2. En déduire la mesure de l’angle \(\widehat{BA_1A_4}\).
Indication : Trouver l’angle au centre interceptant le même arc.
3. De la même manière, trouver la mesure de l’angle \(\widehat{BA_3A_4}\).
4. Quelle est la mesure de l’angle \(\widehat{A_1BA_3}\) ?
Indication : Trouver la nature du triangle \(A_3BA_1\)
5. De la même manière, trouver la mesure de l’angle \(\widehat{A_1BO}\).
6. Quelle est donc la mesure de l’angle \(\widehat{OBC}\) ?
7. Justifier que \(\widehat{ACB}=90^\circ\).
8. En déduire que \(ABC\) est isocèle en \(C\).
9. Conclure.


Démonstration avec le produit scalaire
Préliminaires
1. Démontrer que pour tout vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) :
\[\overrightarrow{u}\cdot\overrightarrow{v}=\frac{1}{2}(\|\overrightarrow{u}\|^2+\|\overrightarrow{v}\|^2-\|\overrightarrow{u}-\overrightarrow{v}\|^2)\]
Preuve: $$
\begin{align*}
\|\overrightarrow{u}-\overrightarrow{v}\|^2&=(\overrightarrow{u}-\overrightarrow{v})\cdot(\overrightarrow{u}-\overrightarrow{v})\\
&=\overrightarrow{u}\cdot\overrightarrow{u}+\overrightarrow{v}\cdot\overrightarrow{v}-2\overrightarrow{u}\cdot\overrightarrow{v} \\
&=\|\overrightarrow{u}\|^2+\|\overrightarrow{v}\|^2-2\overrightarrow{u}\cdot\overrightarrow{v}\\
\overrightarrow{u}\cdot\overrightarrow{v}&=\frac{1}{2}(\|\overrightarrow{u}\|^2+\|\overrightarrow{v}\|^2-\|\overrightarrow{u}-\overrightarrow{v}\|^2)
\end{align*}$$
2. Démontrer que pour tout triangle ABC :
\[BC^2=AB^2+AC^2-2AB\times AC\times cos(\widehat{BAC}) \hspace{0.5cm}\textrm{(Al-Kashi)}\]
Indication : Écrivez de deux manières différentes le produit scalaire \(\overrightarrow{AB}\cdot\overrightarrow{AC}\)
Preuve : $$\begin{align*}
\overrightarrow{AB}\cdot\overrightarrow{AC}&=\frac{1}{2}(AB^2+AC^2-BC^2) \\
\overrightarrow{AB}\cdot\overrightarrow{AC}&=AB\times AC\times cos(\widehat{BAC})\\
AB\times AC\times cos(\widehat{BAC})&=\frac{1}{2}(AB^2+AC^2-BC^2) \\
BC^2&=AB^2+AC^2-2AB\times AC\times cos(\widehat{BAC})
\end{align*} $$
3. En déduire :
\[cos(\widehat{BAC})=\frac{AB^2+AC^2-BC^2}{2AB\times AC}\]
4. Démontrer que pour tout cercle de rayon \(O\) et de diamètre \(AC\), pour tout \(B\) appartenant à ce cercle, le triangle \(ABC\) est rectangle en \(B\)(Théorème de la médiane)
Preuve : $$
\begin{align*}
\overrightarrow{BA}\cdot \overrightarrow{BC} &=(\overrightarrow{BO}+\overrightarrow{OA})\cdot(\overrightarrow{BO}+\overrightarrow{OC})\\
&=BO^2+\overrightarrow{BO}\cdot(\overrightarrow{OA}+\overrightarrow{OC})-OA\times OC\\
&=\left(\frac{AC}{2}\right)^2-\left(\frac{AC}{2}\right)^2\\
\overrightarrow{BA}\cdot \overrightarrow{BC}&=0
\end{align*}$$
Démonstration
1. Montrer que le rayon du cercle \(C_2\) vaut \(\sqrt{3}r\).
Preuve : Les triangles \(OAA_1\) et \(OAA_2\) sont équilatéraux.
\[\widehat{A_1AA_2}=\widehat{A_1AO}+\widehat{OAA_2}=\frac{\pi}{3}+\frac{\pi}{3}=\frac{2\pi}{3}\]
$$\begin{align*}
(A_1A_2)^2&=(AA_1)^2+(AA_2)^2-2AA_1\times AA_2 \times cos(\frac{2\pi}{3})\\
(A_1A_2)^2&=r^2+r^2-2r^2\times\frac{-1}{2}=3r^2 \\
A_1A_2&=\sqrt{3}r
\end{align*} $$
2. Montrer que \(\widehat{OBA_1}=\frac{\pi}{6}\).
Preuve : $$
\begin{align*}
cos(\widehat{OBA_1})&=\frac{(BA_1)^2+OB^2-(OA_1)^2}{2BA_1 \times OB} \\
cos(\widehat{OBA_1})&=\frac{3r^2+r^2-r^2}{2\sqrt{3}r^2}=\frac{\sqrt{3}}{2}
\end{align*}$$
3. En déduire que \(A\), \(O\) et \(B\) sont alignés.
Preuve : le triangle \(OBA_1\) étant isocèle, \(\widehat{BOA_1}=\pi-\frac{2\pi}{6}\)
\[\widehat{AOB}=\widehat{AOA_1}+\widehat{A_1OB}=\frac{2\pi}{3}+\frac{\pi}{3}=\pi\]
Donc \(A\), \(O\), et \(B\) sont alignés.
4. Montrer que \(ACBD\) est un rectangle.
Preuve : D’après le théorème de la médiane, les triangles \(ABC\), \(ACD\), \(ADB\) et \(BCD\) sont rectangles respectivement en \(C\), \(A\), \(D\) et \(B\).
5. Montrer que \((BA_3)^2=r^2(6+3\sqrt{3})\).
Preuve :\(\widehat{BOA_3}=\widehat{BOA}-\widehat{AOA_3}=\pi-\frac{\pi}{3}=\frac{2\pi}{3}\)
$$
\begin{align*}
(BA_3)^2 &= r^2+(r+\sqrt{3}r)^2-2r(r+\sqrt{3}r)\times \frac{-1}{2}\\
(BA_3)^2 &=6r^2+3\sqrt{3}r^2
\end{align*}
$$
6. Montrer que \(\left(\frac{3+\sqrt{3}}{\sqrt{6+3\sqrt{3}}} \right)^2=2\).
7. Montrer que \(cos(\widehat{OBC})=\frac{\sqrt{2}}{2}\).
Preuve : $$
\begin{align*}
cos(\widehat{OBA_3})&=\frac{r^2(6+3\sqrt{3})+r^2-r^2(1+\sqrt{3})^2}{2r^2\sqrt{6+3\sqrt{3}}}\\
&=\frac{3r^2+\sqrt{3}r^2}{2r^2\sqrt{6+3\sqrt{3}}}\\
cos(\widehat{OBC}) &=\frac{3+\sqrt{3}}{2\sqrt{6+3\sqrt{3}}}=\frac{\sqrt{2}}{2}
\end{align*}$$
8. Montrer que \(CB=\sqrt{2}r=CA\).
9. Conclure.
Crédits images
Image générée par l’IAG accessible sur le site www.bing.com/images/create.


8h23
Si vous aimez ce genre d’énigme à la règle et au compas, je vous conseille l’application « Euclidea » qui est basée dessus.
12h59
C’est d’ailleurs le 1.7 de la série ALPHA de EUCLIDEA…