À propos des produits vectoriels

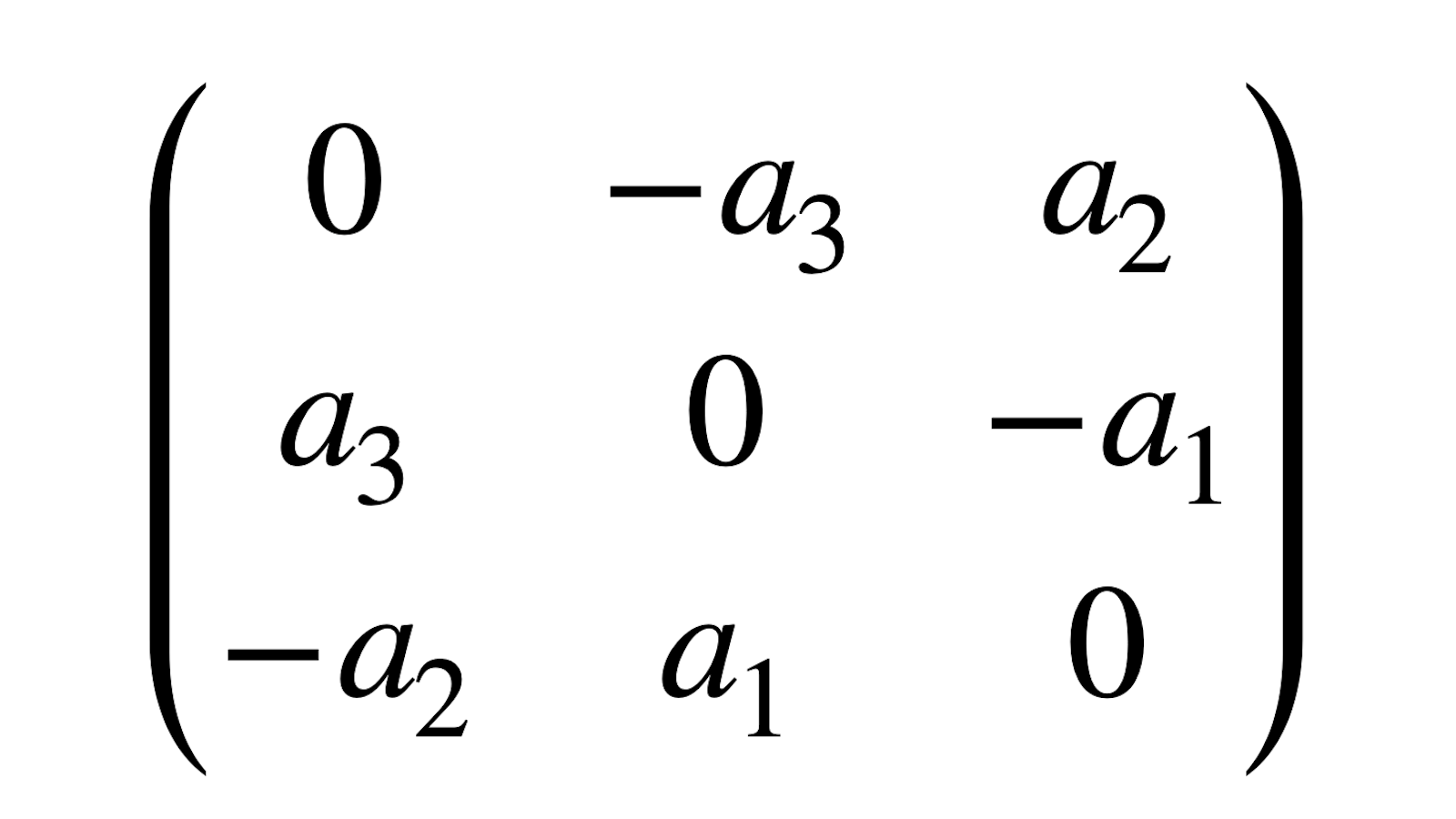
Ce billet est consacré à quelques remarques que j’ai eu l’occasion de faire à propos de la notion de produit vectoriel. Il est écrit pour les lecteurs de IdM qui connaissent un peu d’algèbre.

J’ai toujours été fasciné par le produit vectoriel. Il a de belles propriétés qui étonnent lorsqu’on les rencontre pour la première fois car elles sont fort différentes de celles des opérations arithmétiques auxquelles on est habitué.

Dans \(\mathbb{R}^3\), le produit de \(a=(a_1,a_2,a_3)\) et \(b=(b_1,b_2,b_3)\) est
\[a\wedge b=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)\]

En plus d’être bilinéaire et antisymétrique, il vérifie une identité remarquable, la formule du double produit vectoriel:
\[a\wedge (b\wedge c)=(a\cdot c)b-(a\cdot b)c\]

dans laquelle le «point centré» représente le produit scalaire :
\[a\cdot b=a_1b_1+a_2b_2+a_3b_3\]

Ceci s’étend en fait à tout espace vectoriel réel \(E\) de dimension 3 muni d’un produit scalaire \(g\) et d’une orientation. Avec ces données, on peut en effet doter \(E\) d’une multiplication ayant les mêmes propriétés que le produit vectoriel de \(\mathbb{R}^3\). On la note d’ailleurs avec le même symbole, le «wedge» \(\wedge\), et on l’appelle aussi produit vectoriel ¹Elle est caractérisée par sa table de multiplication. Dans toute base orthonormée directe \((\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3)\) de \(E\), celle-ci se résume à
\[\mathbf{e}_1\wedge\mathbf{e}_2=\mathbf{e}_3,\quad \mathbf{e}_2\wedge\mathbf{e}_3=\mathbf{e}_1,\quad \mathbf{e}_3\wedge\mathbf{e}_2=\mathbf{e}_1\]
ce qui revient à dire qu’on calcule ce produit dans de telles bases de la même manière que le produit vectoriel de \(\mathbb{R}^3\)..

Tous ces produits vérifient l’identité du double produit vectoriel, à condition de remplacer dans la formulation originale de celle-ci le produit scalaire de \(\mathbb R^3\) par \(g\).

Cette formule, qui a des conséquences importantes, m’a toujours intrigué et je me suis demandé jusqu’à quel point elle est caractéristique autrement dit, si les produits construits ci-dessus sont les seuls à la vérifier.

Formellement, on aimerait savoir quels produits antisymétriques \(\tau\) définis sur un espace vectoriel \(V\), réel et de dimension finie \(n>1\), et quelles formes bilinéaires \(\beta\) sur \(V\) peuvent tenir les rôles du produit vectoriel \(\wedge\) et du produit scalaire \(g\) et, en particulier, vérifier l’identité :

\[\tau(u,\tau(v,w))=\beta(u,w)v-\beta(u,v)w\]

Il s’avère qu’on peut classifier tous ces triples \((V,\tau,\beta)\). Je n’ai guère la place ici pour expliquer le résultat complet – ce n’est d’ailleurs peut-être pas l’endroit pour le faire – et je me bornerai donc à décrire les solutions pour lesquelles \(\beta\) est non dégénéré. Dans ce cas, \(n\) vaut nécessairement 3 et, à isomorphisme près, il y a exactement deux triples répondant aux conditions imposées.

Ce fut pour moi une réelle surprise : le traditionnel produit vectoriel avait donc un frère jumeau dont j’ignorais l’existence jusqu’il y a peu. J’en ai par la suite trouvé trace dans un tout autre contexte, dans le beau petit livre Hyperbolic Geometry}de Birger Iversen ²London Math. Soc., Students Texts 25, 1992, Cambridge University Press.. Je vais vous le présenter dans un instant.

Une conséquence de l’identité du double produit vectoriel, assez simple à obtenir, est que \(\beta\) est complètement déterminé par \(\tau\) et, en particulier, qu’il est symétrique. Ceci implique à son tour que \(\tau\) vérifie une autre identité remarquable, appelée identité de Jacobi :

\[\tau(u,\tau(v,w))+\tau(v,\tau(w,u))+\tau(w,\tau(u,v))=0\]

(on l’établit en appliquant l’identité du double produit à chacun de ses termes). Ainsi, compte tenu de l’antisymétrie de \(\tau\), \(V\), muni de la multiplication \(\tau\), est ce qu’on appelle une algèbre de Lie .

Beaucoup d’algèbres de Lie sont des sous-espaces de l’ensemble des matrices carrées, réelles ou complexes. Leur produit, appelé crochet de Lie , est alors le commutateur des matrices

\[(A,B)\mapsto [A,B]=AB-BA\]

Nos deux jumeaux sont isomorphes à des algèbres de Lie de matrices bien connues.

Les produits vectoriels «classiques» \((E,\wedge)\), ceux dont j’ai parlé au début de ce billet, sont isomorphes à l’algèbre des matrices carrées de taille \(3\) à coefficients réels et antisymétriques, qu’on note usuellement \(so(3)\) ³De manière précise, on obtient un isomorphisme explicite en faisant correspondre à \(a\in E\) la matrice représentant l’application \(x\mapsto a\wedge x\) dans une base orthonormée directe de \(E\). :

\[
\begin{pmatrix}
0&-a_3&a_2\\
a_3&0&-a_1\\
-a_2&a_1&0
\end{pmatrix}
\]

Ce n’est pas bien difficile à vérifier ce que, conformément à l’esprit de ce billet, nous ne ferons pas.

Le «jumeau» est quant à lui isomorphe à l’algèbre \(sl(2,\mathbb{R})\) des matrices réelles de dimension \(2\) et de trace nulle :
\[
\begin{pmatrix}
a&b\\
c&-a
\end{pmatrix}
\]
et \(\beta\) est une forme bilinéaire de signature \((+,-,-)\).

La base naturelle
\[
e=
\begin{pmatrix}
0&1\\
0&0
\end{pmatrix},\quad
h=
\begin{pmatrix}
1&0\\
0&-1
\end{pmatrix},\quad
f=\begin{pmatrix}
0&0\\
1&0
\end{pmatrix}
\]
vérifie la table de multiplication
\[
[h,e]=2e,\quad [e,f]=h,\quad [h,f]=-2f
\]
Elle n’est pas «orthonormée» pour \(\beta\) mais
\[
e_1=\frac 1 2(f-e),\quad e_2=\frac 1 2 (f+e), \quad e_3=\frac 1 2 h
\]
l’est en ce sens que dans celle-ci, en effet,
\[
\beta(a,b)=a_1b_1-a_2b_2-a_3b_3
\]
De plus

\[[e_1, e_2]=-e_3,\quad [e_2,e_3]=e_1,\quad [e_3,e_1]=-e_2\]

Ces relations subsistent dans toute base orthonormée de même orientation que \((e,h,f)\) et définissent le personnage à propos duquel je souhaitais vous dire ces quelques mots.