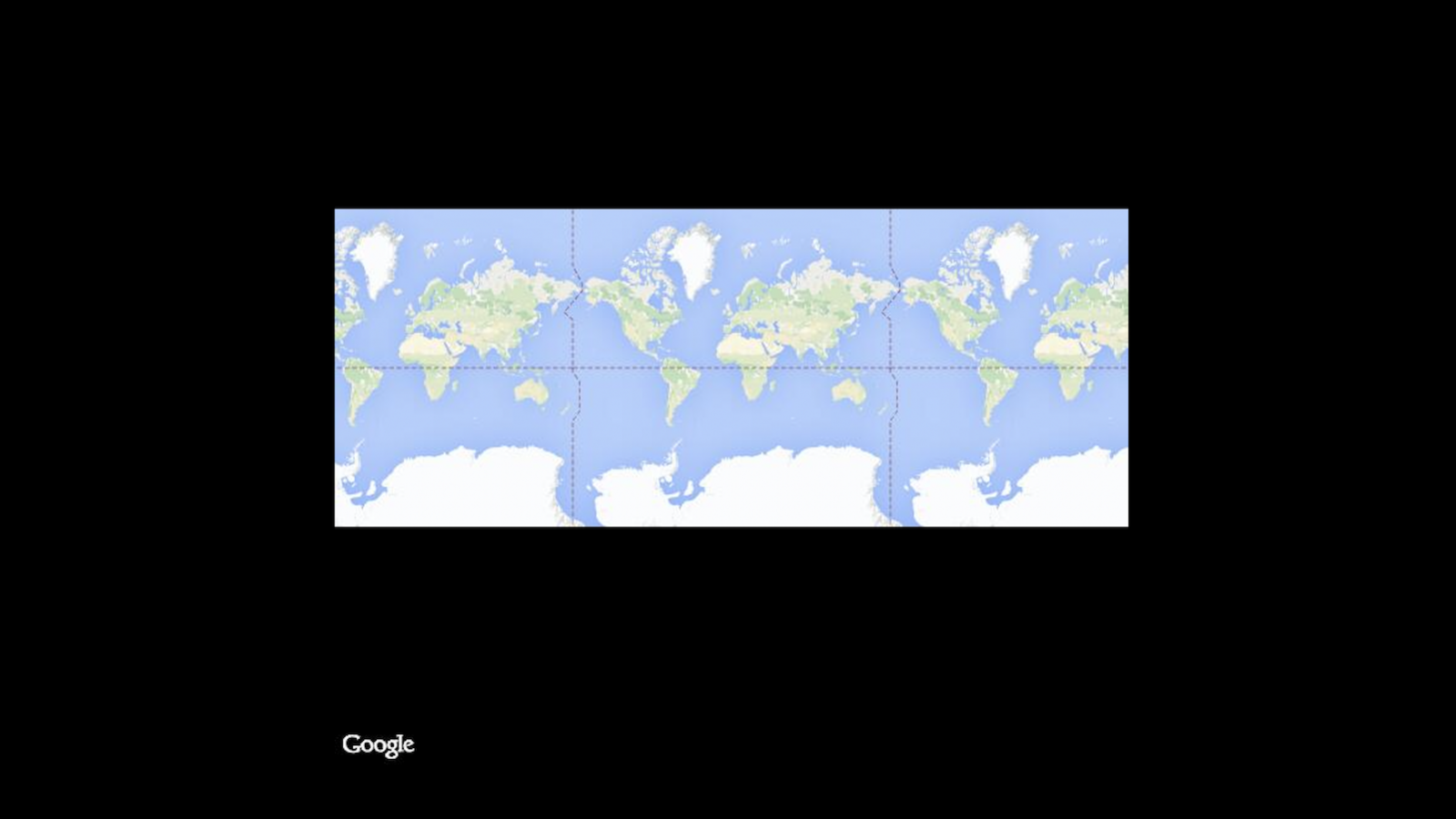
Mais pourquoi donc la carte du monde de Google Maps est-elle aussi laide ?
La carte qui illustre ce billet représente le monde vu de Google Maps. Mais pourquoi donc cette carte est-elle si laide ? En effet il va être difficile de se convaincre, en regardant la carte, que l’Islande et l’Irlande ont presque la même surface ou que le Groenland est environ huit fois plus petit que l’Amérique du Sud.
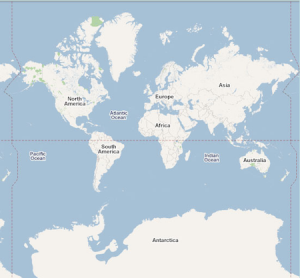
Une des difficultés de la cartographie est de représenter sur un plan (et donc en 2D) le globe terrestre (i.e. un objet en 3D). Le quadrillage régulier des latitudes et des longitudes est caractéristique de la projection du mathématicien et géographe Gérard Mercator .
Le principe est simple : on entoure le globe terrestre avec une feuille papier roulé en cylindre et tangent à l’équateur. Les parallèles sont dessinées comme des droites horizontales parallèles, les méridiens sont dessinés comme des droites perpendiculaires aux parallèles (donc ils sont parallèles entre eux alors que dans la réalité les méridiens se rejoignent aux pôles). Le quadrillage sur la carte correspond aux méridiens et parallèles.
Reste maintenant à projeter les points du globe sur la feuille de papier et c’est là que les choses se compliquent. Le principe de la projection de Mercator est qu’elle est conforme, c’est-à-dire qu’elle conserve les angles (d’autres projections conservent les surfaces et enfin certaines conservent la distance entre les méridiens, voir par exemple ici). La présentation des formules pour obtenir cette projection est un joli exercice de géométrie. Les parallèles qui dans la réalité ont un écartement régulier (par exemple un degré d’angle) vont sur la carte s’écarter de plus en plus à partir de l’équateur, donc il va y avoir un étirement nord-sud. Comme les méridiens sont perpendiculaires sur la carte il va aussi y avoir un étirement ouest-est. Ces étirements vont être de plus en plus importants en s’éloignant de l’équateur et infinis en arrivant aux pôles. On ne peut donc pas représenter les latitudes extrêmes.
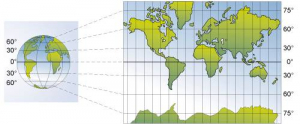
Une erreur classique est de représenter un point du globe par l’intersection de la feuille de papier avec la demi-droite partant du centre de la Terre et le point du globe. Cette projection n’est pas conforme : par exemple un cercle sur le globe terrestre devient une ellipse sur la carte. Ce n’est donc ni une projection de Mercator, ni une projection conforme.
Les puristes pourront faire remarquer que la terre est plus ellipsoïdale que sphérique et accuser Google d’une deuxième mort de Gérard Mercator car l’algorithme utilisé est une variation autour de la projection de Mercator (mais je ne suis pas persuadé que ça change grand-chose. Sauf peut-être pour se retrouver dans le vaisseau du docteur Who.)
Cette projection était très populaire au XVIème siècle car elle préserve les angles (et donc les caps) et c’était pratique pour la navigation. Et comme à cette époque les marins s’aventurent rarement aux pôles ce n’était pas bien grave.
Mais alors pourquoi Google Maps choisit cette représentation ? Car elle permet une représentation rapide des cartes à différentes échelles. La carte est décomposée en tuiles. Chacune tuile est projetée, pré-dessinée et affichable indépendamment les unes des autres, en fonction de la zone choisie par l’utilisateur. La projection utilisée préserve les angles droits entre parallèles et méridiens : on peut donc accoler les tuiles sans problème de continuité. On en déduit donc que la carte proposée n’est qu’une portion d’un planisphère interne à Google Maps. Le navigateur se contente, à un niveau de zoom donné (il en existe 18 actuellement sur Google Maps), d’appeler des tuiles préexistantes. Les carrés ne changent pas en fonction du centre.
Le principe de conservation des angles (représentation conforme) est pratique pour définir un itinéraire. Ceci permet aussi de garder les orientations des rues dans les villes du Nord. Deux rues parallèles à Ny-Ålesund ou à Puero Toro restent parallèles.
Et donc au final Google Maps est peut-être laid pour représenter des cartes mais pour naviguer, c’est difficile de faire mieux.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.