Un théorème qui a du chien…

Écrit par François Sauvageot

Publié le 23 février 2011

Un théorème énoncé par un chien… et qui se démontre avec les Sudoku

Le conte de Jacques Roubaud

Dans « La princesse Hoppy » ou le conte du Labrador ¹, Jacques Roubaud raconte une histoire un brin loufoque mettant en scène des rois qui complotent, des reines qui compotent (parce que les rois complotent sans « elles », ou plutôt sans « l »), une princesse et un chien qui jouent avec une balle et un vieux roi, Uther, qui sur son lit de mort donne l’ordre aux rois de comploter selon la règle de Saint Benoit.

J’ai donné à lire ce texte à mes étudiant(e)s dans le cadre de la préparation à l’analyse de dossier scientifique, une épreuve des concours d’entrée dans certaines écoles d’ingénieurs. La raison en est que le texte illustre en partie quelques questions liées à une notion importante, la notion de groupe. Ici le groupe est mentionné, il ne s’agit d’une contrainte d’écriture ou de toute autre forme poétique d’intervention des groupes en littérature.

Voici ce que dit le conte.

Règle de saint Benoît : Soient trois rois parmi vous quatre : le premier roi, le deuxième roi, le troisième roi. Le premier roi est n’importe quel roi, le deuxième roi est n’importe quel roi,… « Le deuxième roi peut-il être le même que le premier ? » interrompit Eleonor. « Of course » dit Uther… le troisième roi est n’importe quel roi. Alors : Le roi contre lequel complote le premier roi quand il rend visite au roi contre lequel complote le deuxième roi quand il rend visite au troisième roi doit être le même roi précisément contre lequel complote le roi contre lequel complote le premier roi quand il rend visite au deuxième, quand il rend visite au troisième. « OK ? » dit Uther « ce n’est pas tout » : Quand un roi rendra visite à un autre roi ils comploteront toujours contre le même roi. Et si deux rois distincts rendent visite à un même troisième, le premier ne complotera jamais contre le même roi que le deuxième. Contre tout roi enfin il sera comploté au moins un fois l’an dans le bureau de chacun des rois. « J’ai dit » dit Uther. « OK ? » Et il mourut.

Il faut dire que les rois ont pour habitude de se rendre visite, en compagnie de la princesse et du chien, puis de s’enfermer dans le bureau du roi qui reçoit afin de comploter. Le conte précise d’ailleurs qu’il arrive qu’un roi s’enferme avec lui-même et que le complot peut avoir pour cible l’un des comploteurs …

Plus loin se pose une question subtile auquel répond le chien. C’est ce qu’on pourrait appeler le théorème du chien.

Le conte dit maintenant que la princesse et son chien auraient bien voulu savoir contre qui complotait l’oncle Imogène quand il rendait visite à l’oncle Babylas et qu’ils s’enfermaient à clé dans le bureau. Et, d’une manière plus générale, la princesse aurait bien voulu savoir, par exemple, si, étant donné deux quelconques de ses oncles, celui de ses oncles contre lequel complotait le premier quand il rendait visite au deuxième était, ou non le même que celui contre lequel complotait le deuxième quand il rendait visite au premier. « Oui » dit le chien. Il avait ramassé la balle sur la pelouse au bas du perron et la tenait, baveuse, au travers de sa gueule. « Ne parle pas la bouche pleine » dit la princesse. « Et pourquoi ça, s’il te plaît ? » « Parce que, dit le chien, un oue a uatre éléents est orcéent coutati. » Il excellait généralement dans le traduction chien-français quand il avait une balle au travers de ses canines. « Ah » fit la princesse.

Il faut préciser que le chien parle en français par ulcérations ², c’est-à-dire en omettant toutes les lettres autres que celles du mot ulcérations, lettres qui se trouvent être les plus fréquentes en français.

Mes étudiant(e)s n’ont pas eu de mal à reconstituer le théorème du chien : Un groupe à quatre éléments est forcément commutatif.

Les tables de loi

C’est ce théorème que je demandais à mes étudiant(e)s de démontrer comme illustration des premières leçons sur les groupes. Un tel groupe est donné par une « table de multiplication ». On se donne donc quatre objets, disons A, B, C et D et on veut faire une table de multiplication qui obéisse à certaines règles, comme la règle de Saint Benoît.

Quand on effectue le produit A*B, le résultat est un élément du groupe.
Quand on effectue le produit A*B*C, le résultat ne dépend du produit qu’on effectue en premier : on peut soit calculer A*B puis multiplier par C, soit calculer B*C puis multiplier par A.
Un des éléments du groupe se comporte comme la multiplication par 1. On peut l’appeler D et on a donc A*D=A et aussi D*A=D.
Enfin on peut faire la multiplication inverse. Par exemple si B est l’inverse de A, on a A*B=D et aussi B*A=D.

Vous l’aurez compris un groupe n’est pas toujours commutatif : on n’a pas toujours A*B=B*A contrairement à la multiplication habituelle. Le théorème du chien dit que, pourtant c’est vrai dans le cas de notre groupe à quatre éléments.

Pour le démontrer, il suffit de faire la table de la loi. Comment faire ? C’est très simple on fait comme un Sudoku. On remplit un carré 4×4 avec des lettres de sorte que chaque case représente le produit de deux éléments :

Pourquoi est-ce un Sudoku ? Eh bien, puisque chaque élément a un inverse, on voit qu’on ne peut pas avoir A*B=A*C. Sinon en multipliant par l’inverse de A, on aurait inverse(A)*A*B=inverse(A)*A*C et comme inverse(A)*A=D, on aurait D*B=D*C. Mais le produit par D ne change rien et on aurait donc B=C, ce qui n’est pas le cas.

Les produits A*A, A*B, A*C et A*D sont donc tous distincts. Autrement dit toutes les lignes de la table de multiplication comportent les quatre lettres A, B, C et D une fois et une seule (tout produit A*B est l’une de ces lettres). Pour la même raison chaque colonne comporte une fois et une seule chaque lettre.

Le théorème du chien et les groupes

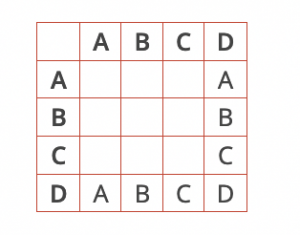
Comment procéder pour trouver toutes les tables de lois possibles ? Tout d’abord on peut remplir la ligne et la colonne de D puisque le produit par D ne fait rien.

Il nous reste à nous occuper des trois autres. Comme chacun a un inverse, que les inverses de deux lettres distinctes sont distincts et que, bien entendu, l’inverse de l’inverse de A est A … on voit qu’au moins l’un des trois autres est son propre inverse. On pourrait dire que c’est comme -1. Appelons-le B. La ligne de B se remplit alors toute seule : on a B*A distinct de D et B puisqu’ils sont déjà sur la ligne, mais aussi de A puisqu’il est sur la colonne … donc B*A=C et il ne reste plus que la possibilité B*C=A :

Et on a alors deux cas, soit l’inverse de A n’est pas A, et c’est donc forcément C et on obtient la table suivante :

soit l’inverse de A est A et alors la table se remplit à nouveau toute seule :

On vérifie que l’on obtient bien des groupes ! Pourquoi sont-ils commutatifs ? Parce que la table de multiplication est symétrique par rapport à la diagonale descendante ! En effet A*B et B*A se trouvent de part et d’autre de cette diagonale et on a donc A*B=B*A si les deux cases comportent la même lettre. Et c’est le cas dans les deux tables … on a donc démontré le théorème du chien !

Les groupes du chien

Quels sont ces groupes ? Il suffit de dessiner un carré pour les illustrer (pas la peine de mettre le carré à plat, n’importe quelle position fera l’affaire !). Mettez quatre couleurs différentes aux quatre coins du carré. Ce qui nous intéresse est la position des couleurs.

Le premier groupe correspond aux rotations d’un quart de tour, d’un demi-tour, de trois quart de tours et de quatre quarts de tour (c’est-à-dire que le carré se retrouve à la même position !). Les lettres A, B, C, D correspondent aux quatre positions possibles des quatre couleurs. Si ces couleurs sont (rouge, vert, bleu, jaune) et si on les décrit en tournant dans le sens des aiguilles d’une montre à partir de la position où se trouve le coin rouge au départ, on a : A=(vert, bleu, jaune, rouge), B=(bleu, jaune, rouge, vert), C=(jaune, rouge, vert, bleu) et D=(rouge, vert, bleu, jaune). On voit que les couleurs tournent en rond !

Le second groupe correspond aux symétries : la symétrie par rapport à une diagonale (échange de rouge et bleu), la symétrie par rapport à l’autre diagonale (échange de vert et jaune), la symétrie par rapport au centre du carré (échange simultané de rouge avec bleu et de vert avec jaune), et puis l’absence de symétrie (les couleurs ne bougent pas).

Les rois forment-ils un groupe ?

Mais au fait ? Pourquoi est-ce que les rois du conte forment un groupe ? Eh bien, c’est là que le bât blesse ! En fait ce n’est pas évident de trouver une loi dans tout ça. On peut faire comme avec les couleurs : les faire tourner ou les échanger. On dit qu’on fait agir un groupe (le groupe des rotations, le groupe des symétries). Mais a-t-on vraiment un groupe ?

La règle de Saint Benoît est ce qui permet d’espérer construire une loi. Ainsi Imogène*Eléonor sera par définition le roi contre lequel Eléonor complote quand il se rend dans le bureau d’Imogène.

Le fait que « Quand un roi rendra visite à un autre roi ils comploteront toujours contre le même roi. » veut exactement dire que notre * est bien une loi.

La règle compliquée « Soient trois rois parmi vous quatre […] Le roi contre lequel complote le premier roi quand il rend visite au roi contre lequel complote le deuxième roi quand il rend visite au troisième roi doit être le même roi précisément contre lequel complote le roi contre lequel complote le premier roi quand il rend visite au deuxième, quand il rend visite au troisième. » signifie que le produit A*B*C ne dépend du choix du produit que l’on effectue en premier.

Mais voilà, les deux autres lois ne sont pas celles que l’on attend. Elles disent en substance que l’on a affaire à un Sudoku. Enfin … presque. Elles disent que les lignes sont formées de quatre lettres distinctes. Mais elles ne disent rien sur les colonnes. Et c’est là le souci ! A cause de cette imprécision, l’ensemble des rois ne forme pas nécessairement un groupe !

En sus des deux tables déjà trouvées, en voici deux autres (qui sont les seules à réaffectation près des lettres associées à chacun des rois) :

ou bien

Changer la règle ... ou limiter la schizophrénie ?

Comment redonner raison au chien ? On peut transformer la règle de Saint Benoit. Par exemple on pourrait demander de transformer l’une des deux dernières lois par l’une de celles-ci :

Et si deux rois distincts REÇOIVENT LA visite D’un même troisième, IL ne complotera jamais AVEC le premier contre le même roi qu’AVEC le deuxième.
Contre tout roi enfin il sera comploté au moins un fois l’an PAR chacun des rois QUAND IL REND VISITE À UN AUTRE ROI.

Mais on peut faire autrement : on peut limiter le nombre de rois schizophrènes. Vous aurez sans doute remarqué que D*D=D, et donc que D s’enferme avec lui-même dans le but de comploter … contre lui-même ! Cette personne existe toujours, dans toutes les tables possibles. Mais dans les tables de groupes, il n’y en a qu’un !

La démonstration mathématisée ...

On note R l’ensemble des rois et * la loi. Les deux premières parties de la règle de Saint Benoit disent que \((R,*)\) est un magma associatif.

Et si deux rois distincts rendent visite à un même troisième, le premier ne complotera jamais contre le même roi que le deuxième.

Cette règle dit que tous les éléments sont réguliers à gauche : \(x*a=x*b \Rightarrow a=b\).

Contre tout roi enfin il sera comploté au moins un fois l’an dans le bureau de chacun des rois.

Cette règle dit que pour \(y\) et \(z\) fixés, l’équation en \(x\) donnée par \(y*x=z\) a toujours une solution.

On peut le formuler autrement en considérant les applications de \(R\) dans \(R\) données par multiplication à gauche : à \(y\) dans \(R\), on associe \(Y\) : \(x\to y*x\). Autrement dit on note \(Y(x)=y*x\).

La dernière règle dit que \(Y\) est surjective et la troisième dit qu’elle est injective. Remarquons que ces deux règles sont donc équivalentes puisque \(Y\) est une application de \(R\) dans \(R\) qui est un ensemble fini : injectivité et surjectivité sont équivalentes.

Notre application \(y\to Y\) est donc une application de \(R\) dans \(S(R)\), ensemble des permutations de \(R\). La seconde règle dit alors que \(y\to Y\) est un morphisme de magmas associatifs de \((R,*)\) dans le groupe \((S(R),\circ)\). Notons \(R’\) l’image de \(R\) par ce morphisme. C’est un sous-magma fini de \((S(R),\circ)\) et donc [c’en est un sous-groupe->567] ! C’est ce sous-groupe qui opère sur les rois, en fait. On a récupéré une action de groupe, mais pas une structure de groupe sur \(R\).

Si l’application \(y\to Y\) est injective, on peut faire un transport de structure de \(R’\) sur \(R\) et on récupère une structure de groupe sur \((R,*)\). Et alors ce groupe est commutatif : c’est soit le groupe de Klein, soit un groupe cyclique. Le problème est qu’on a aucun moyen de montrer que \(y\to Y\) est injective. Ce serait le cas si on reformulait la troisième ou la quatrième partie de la règle. Ce serait en fait le cas si \(R’\) avait bien quatre éléments, en particulier si on a un seul idempotent.

Voici donc la liste des possibilités :
\(R’=\{Id\}\). Autrement dit : \(y*x=x\) et la règle de St Benoit est compatible avec cette loi : quand le premier roi rend visite à un second roi, il complote contre lui-même !
\(R’=\{Id,s\}\) avec \(s\) un élément d’ordre 2. On voit facilement que les fibres de \(y\to Y\) ont même cardinal. On a alors \(R=(e_1,e_2,a_1,a_2)\). Quitte à renuméroter, \(s\) est l’application qui échange les \(e\) et les \(a\) de même indice. La loi s’écrit : \(e_i*e_j=e_i\), \(e_i*a_j=a_j\), \(a_i*e_j=a_j\) et \(a_i*a_j=e_j\).
\(R’\) ne peut avoir trois éléments et s’il en a quatre \(y\to Y\) est injective.

Commentaires

Écrire un commentaire

Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .

Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.