Quand les oies dessinent des arbres

• Arbre

Un vol d’oies bien insolite est l’occasion de parler de désir mathématique et de contextes inattendus.

Bien des interprétations sont possibles du titre « Images des mathématiques ». Par exemple, il peut s’agir d’images produites par les mathématiciens, de présentations imagées de l’activité mathématique ou d’images faisant penser aux mathématiques.

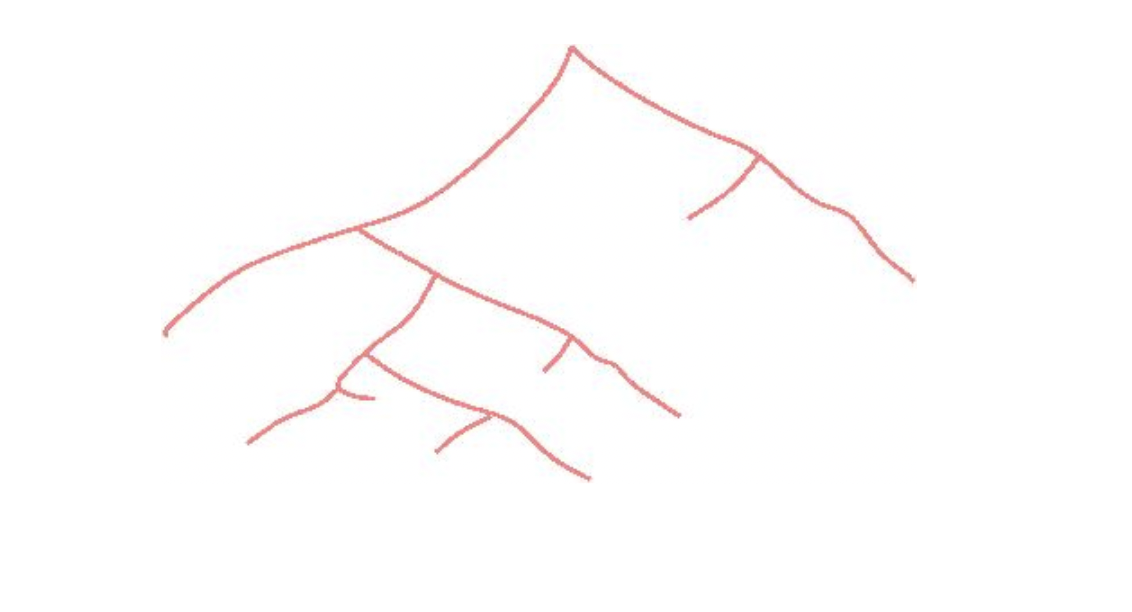
Je voudrais présenter ici une image de la dernière sorte, que j’ai découverte l’été dernier en visitant une exposition de photographies ¹Il s’agit de l’exposition « Régénération2-Photographes de demain », au Musée de l’Élysée à Lausanne.. Elle est due à Milo Newman ²e tiens à remercier Milo Newman de m’avoir permis d’utiliser cette photo. Il m’a en outre communiqué qu’elle a été prise à la fin du mois de décembre 2007. :

 

Cette photo est intitulée « Pink-footed geese, Norfolk, 2007 » ³Elle fait partie de la série « Till the slow sea rise », dont le titre est extrait d’un vers du poème « A forsaken garden » de C.A.Swinburne.. C’est donc un vol d’oies sauvages … ou bien l’esquisse d’un arbre, au sens donné en mathématiques à ce terme  ? ⁴C’est-à-dire un graphe sans cycle. Il s’agit d’un objet apparaissant dans de nombreuses branches des mathématiques – n’est-ce pas curieux pour un arbre ? – comme en témoigne déjà la quantité importante d’articles de ce site parlant d’arbres.Cet arbre dessiné par des oies m’attira tout de suite. Je n’avais jamais rien vu de semblable.

Ceci me fit penser à un aspect essentiel de l’activité de recherche : on ne s’attelle vraiment à un problème avec la volonté de le résoudre, que si on se trouve attiré par celui-ci. Sans désir d’éclaircir un mystère profondément ressenti on ne se lance pas sur les chemins parfois arides de la recherche. Pour cette raison, on ne commande pas à un chercheur de chercher à résoudre tel problème précis : le désir ne se commande pas.

Comment expliquer à un non-mathématicien que l’on puisse ressentir du désir pour un problème ? J’ai essayé plusieurs fois de le faire, ce qui me fit découvrir à quel point cela est ardu. En effet, la plupart du temps, les souvenirs que mes interlocuteurs avaient de leurs expériences mathématiques scolaires, me donnaient l’impression d’avoir à les convaincre que l’on pouvait ressentir du désir pour un cactus !

Mais face à cette photo, j’eus soudain le sentiment que ces oies dessinatrices pouvaient m’aider. Je pensais qu’il était plus facile pour un non-mathématicien de se sentir intrigué par cet arbre dans le ciel que par un problème ou un phénomène mathématique. Et, par la suite, de sentir le besoin d’en savoir plus et de ne pas pouvoir s’empêcher d’y réfléchir. Mais ceci est précisément ce qui se passe au début d’une recherche mathématique ! Autrement, on ne prend pas suffisamment d’impulsion pour s’envoler dans le monde des idées.

Ce qui se passe encore, c’est que d’innombrables questions surgissent d’elles-mêmes face à l’intrigant problème ou phénomène. Par exemple, devant ce vol d’oies je me posais les questions suivantes :

• Comment se forme une telle structure ? Les “V” élémentaires (encore appelés des chevrons) se forment-ils d’abord, pour s’assembler de telle manière à ne pas se gêner ? Ou bien y a-t-il un phénomène de bifurcation : lorsque les branches d’un “V” s’allongent trop, un nouveau “V” prend-il naissance, qui par la suite peut dériver vers l’arrière, comme cela semble être le cas dans cet exemple ?

• L’angle d’un “V” est-il un invariant de l’espèce ? Dépend-il de la vitesse de vol ?

• Comment est assurée la stabilité en vol de cette structure ? Chaque oie cherche-t-elle à garder plus ou moins fixe sur sa rétine l’image des oies qui la précèdent ?

Je sais que ces questions sont désormais avec moi, qu’elles en feront naître d’autres, et qu’elles me rendent avide d’apprendre tout ce qu’on pourra me raconter à ce sujet. Merci d’avance !

De même que j’ai été intrigué par le fait que des oies dessinent un arbre, bien des recherches sont déclenchées par l’apparition insolite d’une forme connue dans un contexte inattendu. Car une telle apparition peut éveiller l’action subtile de l’imagination et du désir de compréhension, sans lesquels il n’y a ni découvertes, ni démonstrations.